Цвет: сложные ответы на простые вопросы

Известно, что на любой вопрос можно дать простой, понятный, убедительный неправильный ответ. Временами этот ответ столь прост и убедителен, что его очевидной неправильности попросту не замечают миллиарды людей.

Сегодня я хотел бы рассказать об одном таком простом вопросе и о двух ответах на него: простом, всем известном, но неправильным; и сложном, непонятном, но правильном.

Это рассказ о цветах. Все мы знаем ещё с детства, что белый свет можно разложить в радугу; а затем из цветов радуги можно собрать как обратно белый свет, так и любой другой цвет, воспринимаемый глазом. Более того, мы твёрдо уверены, что любой цвет можно получить, имея всего три базовых цвета — например, красный, зелёный и синий. Мы проделывали это сотни раз с акварельными красками, и сейчас читаем этот текст с экрана монитора, построенного на этом нехитром принципе.

Также все мы со школы знаем, что белый свет — это смесь световых волн разной длины. Используя тот факт, что волны разной длины по-разному преломляются, мы, с помощью призмы, можем получить «чистый» свет с конкретной заданной длиной волны. Каждому из базовых цветов соответствует своя конкретная длина волны; например, красному соответствует свет с длиной волны 635-700 нм, оранжевому — 590-635 нм, жёлтому — 560-590 нм.

Эти два факта отлично известны любому школьнику. Однако почему-то никто не замечает очевидного противоречия между этими двумя фактами. А именно: если мы возьмём монохромный красный свет (скажем, 650 нм) и смешаем с монохромным жёлтым светом (допустим, 570 нм) мы никак не можем получить оранжевый свет с длиной 610 нм — длины волн не складываются и не усредняются, мы просто получим смесь из 650- и 570-нм волн! Тем не менее, если смешать желтую краску с красной — мы получим оранжевую, и это тоже совершенно несомненно.

Это противоречие занимало меня довольно долго, и вот в один прекрасный день я всё же решил выяснить, как так получается. Предупрежу заранее, что дальше идёт скучный, сложный, неинтересный правильный ответ.

Итак, вышесказанное совершенно верно: волны не перемешиваются и длины их не усредняются. При смешивании чистых цветов мы не получаем новые чистые цвета, а линейчатые спектры разной сложности.

Учитывая, что длины волн меняются непрерывно (т.е. мы имеем бесконечное число «простых» цветов), то множество возможных спектров, которые мы можем наблюдать, является бесконечномерным (гильбертовым) пространством. Это пространство обозначается H_color и представляет собой бесконечномерный конус. Каждая точка этого конуса является функцией C(w); здесь w — длина волны света (изменяется примерно от 390 до 700 нм), а значением C(w) является интенсивность нашего спектра для этой длины волны.

Глаз воспринимает цвета благодаря специальным клеткам — колбочкам. Существуют колбочки трёх видов: S, M и L. Каждый тип колбочек реагирует на свет определённой длины волны: S на короткие волны (с пиком в районе 430 нм), M на средние волны (540 нм), L на длинные волны (570 нм).

Если бы колбочки были чувствительны только к «своей» волне, абсолютное большинство предметов были бы для нас бесцветны; т.е. например свет с длиной волны 500 нм не воспринимался бы колбочками совсем. Однако, к счастью для нас, каждый из типов колбочек чувствителен к определённой довольно широкой части спектра.

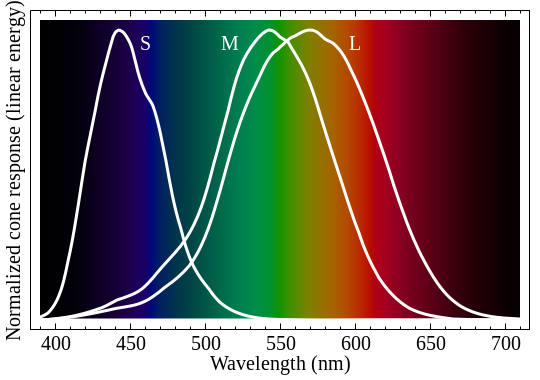
Математически мы можем обозначить «отзывчивость» каждого типа колбочек на свет определённой длины волны как некоторые «функции отзывчивости» — s(w), m(w) и l(w). Тогда мы можем факторизовать наше пространство H_color, введя отношение эквивалентности: цвета C(w) и C'(w) совпадают, если совпадают тройки интегралов
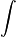[C(w) * s(w), 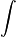C(w) * m(w), 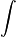C(w) * l(w)]
и
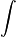[C'(w) * s(w), 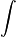C'(w) * m(w), 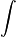C'(w) * l(w)].

Таким образом, наш глаз сворачивает бесконечномерный конус физических цветов в трёхмерный конус воспринимаемых цветов, который принято обозначать R³_color. Каждому наблюдаемому цвету соответствует, таким образом, бесконечное количество физических цветов — иными словами, существует бесконечное множество спектров, воспринимаемых глазом как один и тот же цвет. Такие цвета, которые физически различны, но человеком воспринимаются одинаково, называются метамерами.

Любопытно, что разложение цвета на три составляющие (трихроматизм) широко распространено в природе, но это не единственный вариант цветового зрения. Существуют виды с тетрахроматическим и даже пентахроматическим зрением — например, глаз голубя содержит пять различных видов светочувствительных клеток.

Важнейшее свойство нашего зрения — его аддитивность: если сложить любые метамеры жёлтого и красного цветов, мы получим метамер оранжевого цвета. Без этого свойства зрения все современные способы передачи цвета просто не работали бы.

Когда вы рассматриваете фотографию на экране вашего монитора, вы на самом деле видите совершенно не тот же спектр и не те же физические цвета, что были в оригинале — вы видите специальным образом подобранный набор метамеров, который воспринимается мозгом как идентичный оригинальному.

Отсюда, кстати, следует малоизвестный факт: фотография НЕ сохраняет точный визуальный образ объекта; такой образ годится только для нашего глаза, но не для научного исследования. Точный спектр, а не его цветовое восприятие, чрезвычайно важен во многих научных областях — например, в астрономии, поэтому астрономы пользуются спектрометрами (если нужен спектр), черно-белыми ПЗС-матрицами (если интересует интенсивность света) или снимают искомый объект в каком-то конкретном узком диапазоне длин волн. Многие «цветные» астрономические фотографии на самом деле попросту раскрашены.

Вернёмся, однако, к нашему зрению. Фактически, каждый наблюдаемый человеком цвет характеризуется тремя величинами — интенсивностями воздействия на каждый из трёх типов колбочек.

Первая попытка построить такой конус наблюдаемых цветов относится к 1931 году. Международная комиссия по освещению (Commission internationale de l’éclairage, CIE) построила т.н. цветовое пространство CIE 1931. Выглядит оно следующим образом:

Это некоторое сечение истинного R³_color конуса плоскостью равной интенсивности. Поскольку человек считает, что светло-серый и тёмно-серый — это один и тот же цвет, просто разной яркости, мы можем ограничиться рассмотрением цветов одной плоскости.

Здесь по оси x отложена нормализованная интенсивность воздействия на L-клетки, по оси Y — на M-клетки; интенсивность воздействия на S-клетки определеляется как 1 — x — y.

Эта двумерная фигура определяет все метамеры, видимые обычным человеком. Внешняя кривая (спектральный локус) соответствует «чистым» монохромным цветам. Точка (1/3, 1/3) — белый свет.

Прямая, соединяющая концы спектрального локуса — линия пурпурных цветностей. Находящихся на ней цветов нет в радуге, их можно получить только смешиванием монохромных цветов.

Из CIE 1931 можно получить классические цветовые пространства RGB. Для этого нужно выбрать три точки на спектральном локусе, например, вот так:

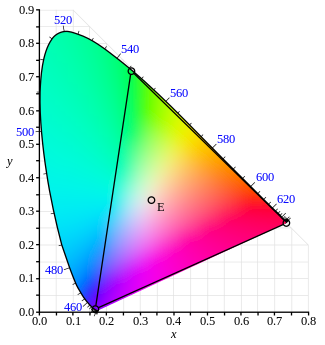
И задаться функциями соответствия:

Эти кривые описывают интенсивности базовых цветов, которые необходимо приложить для получения метамера чистого монохроматического света с заданной длиной волны.

Про цветовые пространства, гамуты разных устройств передачи цвета и восприятие цветов человеческим мозгом можно рассказать ещё кучу всякого интересного, но позвольте мне оставить это на внеклассное чтение 🙂
en.wikipedia.org/wiki/Color_vision
en.wikipedia.org/wiki/CIE_1931_color_space