Фильтрация ложных соответствий между изображениями при помощи динамического графа соответсивий

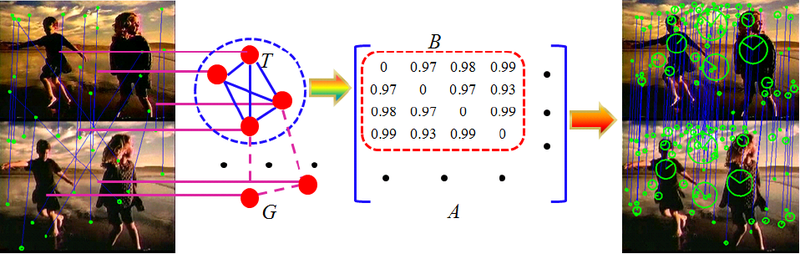
Многие современные алгоритмы компьютерного зрения строятся на основе детектирования и сопоставления особых точек визуальных образов. По этой теме было написано немало статей на хабре(например SURF, SIFT). Но в большинстве работ не уделяется должного вниманию такому важному этапу, как фильтрация ложных соответствий между изображениями. Чаще всего для этих целей применяют RANSAC-метод и на этом останавливаются. Но это не единственный подход для решения данной задачи.
Данная статья посвящена одному из альтернативных способов фильтрации ложных соответствий.

Постановка задачи

Пусть имеем два набора особых точек полученных с двух изображений P и Q с n_p и n_q точками соответственно.Каждая особая точка представляет собой пару p={p_d, p_c}. p_d — представляет собой местную особенность точки(например SURF-дескриптор), а p_c={x,y} — координаты особой точки.
Имеем множество соответствий M={c_i = (i, i’) | c_i ∈ C, i ∈ P, i’ ∈ Q}, построенное при помощи некоторой метрики(например как точки с ближайшими по Евклидовой метрике дескрипторами). Для каждого соответствия построим неотрицательную функцию оценки S_ci=f₁(i_d, i’_d).

Для двух соответствий c_i=(i, i’) и c_j=(j, j’) предположим, что расстояние между точками i и j на первом изображении и точками i’ и j’ на втором изображении l_ij и l_i’j’ соответственно. Очевидно, что если эти два соответствия верные, то мы можем выровнять изображение Q по отношению к P с масштабным коэффициентом l_ij frasl; l_i’j’, и мы говорим что эта пара соответствий голосует за масштаб l_ij frasl; l_i’j’. Теперь предположим, что имеется визуальный образ с n соответствующих ему правильных соответствий, тогда для каждой пары этих соответствий масштабный коэффициент должен быть примерно одинаковый. Такой масштаб будем называть масштабным коэффициентом геометрической согласованности и обозначать через s. Масштабный коэффициент геометрической согласованности пары соответствий c_i=(i, i’) и c_j=(j, j’) выражается как:
S_cicj(s)=f₂(|l_ij — s*l_i’j’|), где f₂(x) — неотрицательная монотонно убывающая функция.

Пускай множество M содержит m соответствий M={c₁, …, c_m}. Построим граф G с m вершинами, каждая вершина из которого представляет соответствие из M. Вес ребра между вершинами i и j определяется следующим образом:
w_ij(s)=S_ci*S_cj*S_cicj(s).
Построенный таким образом граф будем называть Динамическим Графом Соответствий(далее ДГС).

Взвешенную матрицу смежности для ДГС обозначим A(s) и построим следующим образом:

A(s) ∈ R^m*m — симметрична и неотрицательна.

Правильному визуальному образу, содержащему n особых точек, соответствует полный подграф T ∈ G с n вершинами, который, как нетрудно заметить, является взвешенным дубликатом максимальной клики. Такой подграф имеет высокую среднюю внутри-кластерную оценку:

Если мы представим T в виде индикатор-вектора y такого, что 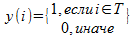, то средняя внутри-кластерная оценка может быть переписана в квадратичной форме:
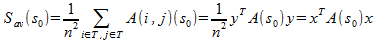, где , .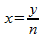

Как известно, теорема Моцкина-Штрауса устанавливает связь между максимальной кликой и локальным максимумом такой квадратичной формы:
, где — стандартный симплекс в R^m. Проще говоря, в теореме говорится, что подмножество T вершин графа G является максимальной кликой тогда и только тогда, когда его характеристический вектор x^T является локальным максимумом квадратичной функции f(x) в стандартном симплексе, где x_i^T = 1⁄|T| если i ∈ T, x_i^T=0 иначе.

Хотя оригинальная теорема Моцкина-Штрауса относится только к не взвешенным графам, Паван и Пелилло обобщили её на взвешенные графы и установили связь между плотными подграфами и локальными максимумами уравнений.

Принятая норма l₁ имеет ряд преимуществ. Во-первых, имеет простой вероятностный смысл: x_i представляет вероятность того, что полный подграф содержать вершину i. Во-вторых, решение x разреженно, и только некоторые компоненты в том-же подграфе имеют большое значение, остальные компоненты имеют достаточно малые значения, что позволяет выделить кластер отбросив те вершины которые являются шумом являющиеся шумом.

Таким образом, задача фильтрации соответствий сводится к задаче отыскания кластеров соответствий, представляющих отдельные зрительные образы. В свою очередь для отыскания таких кластеров необходимо решить описанную выше задачу оптимизации.

Описание алгоритма

Для масштаба s₀, задача оптимизации может иметь много локальных максимумов. Каждый большой локальный максимум чаще всего соответствует правильному визуальному образу, а маленький локальный максимум чаще всего возникает в результате зашумлений.

При инициализации x(1), соответствующее локальное решение x может быть эффективно получено при помощи уравнения самосборки первого порядка, имеющего вид:

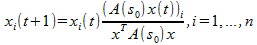
Можно заметить, что симплекс Δ инвариантен относительно такой динамики, а это значит, что любая траектория начинающаяся в Δ, останется в Δ. Кроме того, было доказано, что когда A(s₀) симметрична и с неотрицательными элементами, целевая функция строго возрастает вдоль любой неконстантной траектории уравнения самосборки, и эти асимптотически устойчивые точки находятся в строгом взаимно-однозначном соответствии с локальными решениями квадратичной функции.

Грубо говоря, для того чтобы найти все крупные локальные максимумы x, берут много начальных инициализаций и таким образом гарантируют, что все крупные локальные максимумы на заданном симплексе будут учтены. Как было сказано выше, для нашей задачи каждый локальный максимум соответствует визуальному образу, то он должен обладать двумя свойствами:

1. Свойство локальности. Особые точки одного визуального образа лежат в некоторой небольшой окрестности, поэтому нам необходимо инициализировать x(1) только в окрестности каждой вершины ДГС.
2. Свойство непересечения. Различные визуальные образы, как правило, не содержат общих вершин в G, а это значит, что если два локальных максимума x и y соответствуют двум различным визуальным образам, то (x,y)~0.

Так как мы инициализировали x(1) для каждой вершины ДГС и инициализации вершин одного и того-же визуального образа сходятся к примерно одному локальному максимуму, то мы должны слить локальные максимумы соответствующие одним и тем-же визуальным образам. Благодаря такой избыточности данных достигается дополнительная устойчивость к шумам. Также отбрасываются все малые локальные максимумы соответствующие шумам.

В конце необходимо восстановить визуальный образ для каждого локального максимума x. Т.к. x_i представляет собой вероятность вхождения вершины i в визуальный образ x, мы можем выбирать только те вершины, чье вхождение в визуальный образ наиболее вероятно.

Параметры алгоритма

Как видно из приведенного выше описания, алгоритм имеет большое количество настраиваемых параметров таких, как:

• S_ci=f₁(i_d, i’_d) -функция оценки соответствия
• S_cicj(s)=f₂(|l_ij — s*l_i’j’|) — функция оценки геометрической согласованности соответствий
• Ε — пороговое значение для оценки веса ребра, на предмет принадлежности к окрестности инициализации
• Φ — радиус окрестности для которой берется инициализация x(1)
• Ψ — пороговое значение для оценки малости локального максимума
• Ω — пороговое значение для слияния окрестностей
• Θ — пороговое значение вероятности вхождения вершины в визуальный образ

Эксперименты

Типичные результаты работы алгоритма представлены ниже.

Заключение

Применение описанного алгоритма на практике затрудненно из-за высокой чувствительности к параметрам алгоритма, которые подбираются опытным путем для каждого набора входных данных. Также для эффективного применения данного метода необходим предварительный анализ входного набора соответствий на предмет выделений доминирующих масштабных коэффициентов.
В связи с тем, что борьба с шумами происходит за счет избыточности данных, для работы алгоритма требуется большое количество дополнительной памяти и времени на её обработку.
Поэтому данный алгоритм интересен с точки зрения примененных в нем подходов к анализу соответствий, а не как альтернатива например упомянутому в начале статьи RANSAC-методу.

Литература

• Common Visual Pattern Discovery via Spatially Coherent Correspondences Hairong Liu, Shuicheng Yan, Departament of Electrical and Computer Enginering, National University of Singapore, Singapore
• T. Motzkin and E. Straus. Maxima for graphs and a new proof of a theorem of Turan. Canad. J. Math, 1965.
• 10. M. Pelillo, K. Siddiqi, and S. Zucker. Matching hierarchical structures using association graphs. TPAMI, 1999.

UPD Ссылка на исходники метода: dl.dropbox.com/u/15642384/src.7z