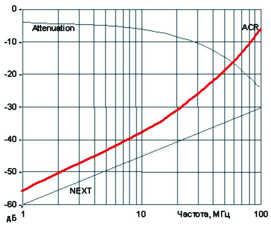
Интерполяция + (линейная | логарифмическая) шкала + С++

Понадобилось мне как-то сделать интерфейс для загрузки в микроконтроллер график функции «сопротивление -> температура» (график решили задавать по нескольким точкам, а потом их интерполировать). По ходу дела выяснилось, что график будет оч-чень нелинейным (180 Ом -> 100^o, 6 000 Ом -> 0^o, 30 000 Ом -> -30^o). Поэтому пришлось мне погрузиться в тему логарифмических шкал… и сразу вынырнуть, так как я не нашел того, что мне нужно. А нужно-то мне было всего лишь понять математику (и реализацию на С++) таких дел. ЧуднО — вроде такая нужная тема, а не расписано! Ну да ладно — мозги заскрипели и вспомнили высшую математику из университета, и программа была написана. Решил описать я свои мытарства тут — может, кому пригодится.

В этой статье я распишу теорию (а также базовые виртуальные классы), в следующей возьмусь за конкретные реализации средствами Qt.

Осторожно: в тексте много графики!

Постановка задачи

Давайте немного подробнее опишем что нам надо:

задание функции — необходимо задать несколько точек, по которым строится график. Вобщем, вспоминаем интерполяцию;
построение графика функции — да-да, я знаю про Qwt. Может, не очень хорошо я его знаю, т. к. я не нашел в нем следующей возможности:
интерактивное задание функции — мне нужно двигать точки, по которым строится функция, прямо на экране, в текущих экранных координатах шкалы, которые переводятся в реальное значение;
линейная/логарифмическая шкала — поскольку значения вот такие, как я написал, мне пришлось заложить возможность менять шкалу. Причем как одну, так и обе сразу.

Вот такое ТЗ… Ну да ничего, я справился! Давайте и вам помогу.

Да, пока не нырнули — спасибо Equation Editor-у от CodeCogs! С их помощью я лихо построил все математические формулы без всяких Microsoft Equation Editor, которые потом надо еще экспортировать в графику со вставкой сюда. Кстати, там есть и русский редактор. В общем, рекомендую!

Ну и если вместо формул вы видите пустые квадратики — это тоже «спасибо» Equation Editor-у…

Прикрепленный Excel-файл

По ходу написания статьи я все расчеты строил и проверял в таблице Excel с формулами. Оказалось очень удобно. И я решил его выложить для общественного пользования. Там внизу перечислены страницы по разделам. На каждой странице параметры, которые можно менять, отмечены как ячейки с желтым фоном. Остальные клетки лучше не трогать. Впрочем, все формулы можно смело смотреть. Скачивайте файлик и пробуйте на здоровье! Если проблемы с файлом — пишите, вышлю.

Функциональная зависимость

Итак, у нас есть некоторая зависимость — обозначим ее как $f(t)$ . Здесь у нас $t$ — горизонтальная ось графика, $f(t)$ — вертикальная. В моем случае $t$ было значение сопротивления, $f(t)$ — температура.

Почему не $y=x$ ? Ведь вроде бы должно быть так? Так-то оно так, но ~~только в школе~~ в простейшем случае.

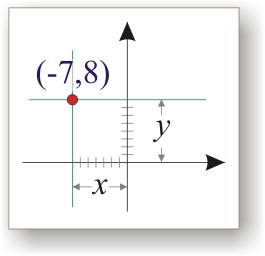
$(y,x)$ — это координаты точки на плоскости. Для простоты определимся использовать Декартову систему координат: $y$ задает вертикальное смещение горизонтальной оси относительно нуля, $x$ задает горизонтальное смещение вертикальной оси относительно нуля.

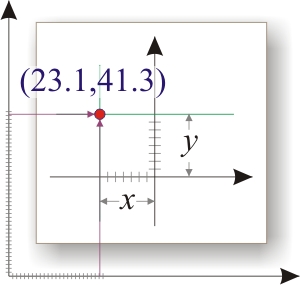Все хорошо тогда, когда мы рисуем на бумаге эту самую систему координат и в ней ставим точки. Там и вправду — выбрали центр, линейкой отложили сюда, потом туда. А вот при построении графика в какой-то программе уже тонкости начинаются — что считать нулем? Что считать за "+", а что за "-"? Я рисую для этой статьи графику в CorelDRAW — там центр считается снизу слева (его можно передвинуть куда надо).

Да и в каких единицах график-то? В сантиметрах? А почему? У меня следующий этап будет реализация на С++ средствами Qt, так там я сделаю окно QWidget, у которого по умолчанию ноль — это слева сверху; единицы измерения — экранные пиксели.

Ну и не забываем о том, что это все эти красивые рассуждения справедливы пока что для линейной шкалы, а у нас маячит за горизонтом логарифмическая. Там вообще черт знает что будет!

Но это только лишь точка. А у нас будет какая-то линия, точнее — много линий. Что там будут за преобразования?

Вот именно поэтому мы с самого начала должны четко разделить функциональную зависимость и преобразования координат.

Итак, давайте договоримся о следующем: у нас есть некоторый абстрактный процесс, который описывается функциональной зависимостью $f(t)$ . При отображении на экран используется преобразование в координаты $(t,f(t))\Rightarrow(X,Y)$ , где $X=X(t)$ , $Y=Y(f(t))$ . Следующие шаги — это прояснить эти самые $X(t)$ и $Y(f(t))$ .

Но отложим пока в сторону координаты — нам надо как-то задать нашу функцию (помните ТЗ)? Причем задать в тех самых абстрактных координатах $(t,f(t))$ . Этим и займемся.

Интерполяция

В моем случае был известен ряд точек $(t,f(t))$ :

$t$ , Ω	$f(t)$ , ˚
180	100
6 000	0
30 000	-30

Не ахти какая сложна и большая таблица, но тут явно куча пустых мест. А какое сопротивление соответствует 60˚, -40˚, …? В общем, надо проставить отсутствующие точки. И в этом нам помогут интерполяция, аппроксимация и экстраполяция. Впрочем, не пугайтесь — одной интерполяции хватит за глаза.

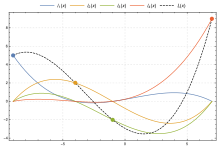Методов интерполяции много, все рассматривать я тут не буду. Лично мне приглянулся вначале интерполяционный многочлен Лагранжа. Он весьма прост в расчете и реализации, а также в настройке. Там предполагается, что задано множество из $n$ точек вида $(x_{i}, y_{i})$ (тут мы на время таки вернемся к заданию точек в виде $(x,y)$ — так уж принято в математике).

Многочлен вычисляется как $L(x)=\sum_{i=0}^{n}y_{i}l_{i(x)}$ , где $l_{i}(x)=\prod_{j=0, j\neq i}^{n}\frac{x-x_{j}}{x_{i}-x_{j}}$ .

Математика испугала? Хм… Ладно, напишу на языке С++:

typedef qreal Real;  Real Lagranj (Real X) { 	static const int n = 3; 	static Real y[n] = {100, 0, -30}; 	static Real x[n] = {180, 6000, 30000}; 	Real L, l; 	int i, j;  	L = 0;  	for (i = 0; i < n; ++i) 	{ 		l = 1;  		for (j = 0; j < n; ++j) 			if (i != j) 				l *= (X - x[j]) / (x[i] - x[j]);  		L += y[i] * l; 	}  	return L; }  int main (int argc, char *argv[]) { 	Real y;  	y = Lagranj (180); 	y = Lagranj (500); 	y = Lagranj (1000); 	y = Lagranj (6000); 	y = Lagranj (10000); 	y = Lagranj (30000); 	y = Lagranj (0); 	y = Lagranj (100000); }

Как видите, все достаточно тривиально (насколько тривиальными могут быть полиномы).

Еще одно большое достоинство полиномов Лагранжа — их легко можно промоделировать в таблице Excel-я, что я и делал.

Потом, правда, все стало немного печально, т. к. у этих полиномов, как и у любых других, на графике видны вибрации. Т. е. они не могут дать прямые линии — постоянные значения. В моем случае я не смог их настроить дОлжным образом — они выгибались в явно недопустимые числа. Поэтому мне пришлось от них отказаться…

Работая в Corel, я был близко знаком с кривыми Безье — тоже достаточно удобное и простое представление табличных данных. Весьма легко реализуется в программировании. Однако это уже не интерполяция, а, скорее, аппроксимация, т. к. тут приходится подгонять кривую к нужному виду.

В итоге, внимательно присмотревшись к своей функции, я понял, что у меня вполне прокатит кусочно-линейная интерполяция — прямые отрезки между заданными линиями. Не то, чтобы совсем уж фен-шуйно, но зато легко реализуемо и удобно настраиваемо.

Говоря языком математики, мы между точками $i$ и $i+1$ проводим прямые линии вида $y=y_{i}+\frac{y_{i+1}-y_{i}}{x_{i+1}-x_{i}}(x-x_{i})=k_{i}*x+b_{i}$ .

Опять же, на языке С++ это будет выглядеть так:

typedef qreal Real;  Real Linear (Real X) { 	static const int n = 3; 	static Real y[n] = {100, 0, -30}; 	static Real x[n] = {180, 6000, 30000}; 	static Real k[n] = {	(y[1] - y[0]) / (x[1] - x[0]), 							(y[2] - y[1]) / (x[2] - x[1]), 							(y[3] - y[2]) / (x[3] - x[2])}; 	static Real b[n] = {	y[0] - k[0] * x[0], 							y[1] - k[1] * x[1], 							y[2] - k[2] * x[2]}; 	int i; 	 	// . за пределами точек? 	if (X <= x[0]) 		return y[0]; 	else if (X >= x[n-1]) 		return y[n-1];  	// . в точках? 	for (i = 0; i < n-1; ++i) 		if (X == x[i]) 			return y[i];  	// . между точками? 	for (i = 0; i < n-1; ++i) 		if (X >= x[i] && X <= x[i + 1]) 			return k[i] * X + b[i];  	return 0;	// ошибка - сюда алгоритм зайти не должен !!!  }  int main (int argc, char *argv[]) { 	Real y;  	y = Linear (180); 	y = Linear (500); 	y = Linear (1000); 	y = Linear (6000); 	y = Linear (10000); 	y = Linear (30000); 	y = Linear (0); 	y = Linear (100000); }

Тоже ничего революционного, не так ли?

Есть одно существенное различие между полиномом Лагранжа и линейной интерполяцией: у первого нельзя явно задать значения за пределами точек — они вычисляются, у второго можно это дело контролировать. Также и поэтому я в конечном итоге остановился на линейном варианте. Более того — в логарифмическом масштабе, к которому я стремился, линейные отрезки дают более подходящий мне вариант.

Впрочем, не будем заморачиваться сейчас на методах интерполяции. Давайте лучше мы сделаем базовый класс, от которого будем наследовать реализации различных методов ~~$#*@!~~поляции.

Базовый класс для задания/расчета функции

Что этот класс должен уметь делать? Мне кажется, что такой класс должен:

давать значение функции в зависимости от аргумента — собственно, ради чего мы его и городим;
реагировать (перемещать и пересчитывать) на изменение точек интерполяции — на вход подается факт нажатия/отпускания в некоторой координате, в результате чего производится пересчет параметров;
различать одиночный и двойной щелчок мышки — одиночное нажатие, как по мне, указывает на передвижение точки; двойное создает новую точку;
прорисовывать точки интерполяции как при их движении, так и без оного — т. к. у разных методов интерполяции будет разное интуитивно понятное значение точек интерполяции, то и выводить их должен производный класс (например, в интерполяции точка является частью графика; в аппроксимации точка не обязательно лежит на графике; в кривых Безье часть точек лежит на графике, часть задают форму);
давать координаты текущей передвигаемой точки — это нужно для вывода текста координаты данной точки;
давать сервисную информацию — например, «определена ли функция?», «сколько точек для интерполяции используется?», «получить координаты точек» и т. п. Эти данные позволят сохранить текущие настройки;
производить настройку — «распределить столько-то точек», «задать координаты точки» — это нам позволит восстановить сохраненные настройки.

Еще есть мысли? Если будут — пишите в комментариях, добавим!

Получается такой вот класс:

class FunctorBase { protected: 	virtual QPointF &get_point (const int Pos) = 0;			// возврат текущей точки 	virtual QPointF get_point (const int Pos) const = 0;	// возврат текущей точки  public: 	// . события 	virtual void MouseClicked (const QPointF &Pt) = 0;		// нажатие на кнопку мышки в координате Pt 	virtual void MouseDblClicked (const QPointF &Pt) = 0;	// двойное нажатие на кнопку мышки в координате Pt 	virtual void MouseReleased (void) = 0;					// отпускание кнопки мышки 	virtual void MouseMove (const QPointF &Pt) = 0;			// передвижение мышки (в режиме перетаскивания кнопки), текущая координата Pt 	virtual void DrawPoints (QPainter &p, const ScaleBase &X, const ScaleBase &Y, const int ptRadius, QPen &pnCircle, QBrush &brCircle) = 0;		// прорисовка всех точек интерполяции, кроме текущей 	virtual void DrawCurPoint (QPainter &p, const ScaleBase &X, const ScaleBase &Y, const int ptRadius, QPen &pnCircle, QBrush &brCircle) = 0;		// прорисовка текущей точки интерполяции (и связанных с ней, если надо)  	// . свойства 	virtual qreal f (const qreal t) const = 0;		// значение функции от аргумента 	virtual QPointF *point (void) const = 0;		// координаты текущей точки; если такой нет - возврат NULL 	virtual bool is_specified (void) const = 0;		// функция определена 	virtual int num_points (void) const = 0;		// количество точек для интерполяции 	QPointF point (const int Num) const;			// координата точки по ее номеру  	// . управление 	virtual bool set_points (const int Num) = 0;	// задание количества точек; возврат успешности операции 	QPointF &point (const int Num);					// координата точки по ее номеру 	void set_point (const int Num, const QPointF &Pt);		// задание координаты точки по ее номеру  	// . перегруженные операторы 	qreal operator() (const qreal t) const		{ return f(t); }			// значение функции от аргумента 	operator bool (void) const					{ return is_specified (); }		// функция определена 	QPointF &operator[] (const int Num)			{ return point (Num); }		// координата точки по ее номеру 	QPointF operator[] (const int Num) const	{ return point (Num); }		// координата точки по ее номеру };	// class FunctorBase  inline QPointF &FunctorBase::point (const int Num) { 	Q_ASSERT_X (Num < num_points (), "receiving points", (QString ("incorrect point index %1 for array size %2 is used"). arg (Num). arg (num_points())).toAscii().constData()); 	return get_point (Num); } inline QPointF FunctorBase::point (const int Num) const { 	Q_ASSERT_X (Num < num_points (), "receiving points", (QString ("incorrect point index %1 for array size %2 is used"). arg (Num). arg (num_points())).toAscii().constData()); 	return get_point (Num); } void FunctorBase::set_point (const int Num, const QPointF &Pt) { 	point (Num) = Pt; }

(Тем, кто недоволен моим стилем и структурой — предложите объективно лучше!)
(Тем, кто найдет ошибки в коде — спасибо!)

Думаю, тут все очевидно.

Для координат используется представление точки в виде QPointF (пара чисел в виде qreal, qreal. «На всех платформах, кроме ARM, используется double» — так написано для Qt 4.8).

Нажатия на кнопки мышки реализованы функциями MouseClicked, MouseDblClicked, MouseReleased и MouseMove. Предполагается, что в конкретных реализациях будут соответствующие реакции.

Для прорисовки точек используются методы DrawPoints и DrawCurPoint. Если для всех методов, кроме этих, координаты используются абстрактные, то тут нужны самые что ни на есть экранные. Поэтому сюда передаются два объекта класса ScaleBase для преобразований. Этот класс — тоже виртуальный. Его предки реализуют преобразование из абстрактных координат в текущие экранные. Сам же этот класс будет описан ниже.

Текущее значение функции возвращает метод f (const qreal) и перегруженная операторная функция operator() (const qreal).

Для задания структуры используются функции set_points (Num) — задание количества точек, point (Num), set_point (Num), get_point (Num) — задание координат конкретной точки. num_points () const — возвращает количество точек, point (Num) const, get_point (Num) const возвращают координаты точки. is_specified () const возвращает true, если структура функции задана.

В следующей статье мы распишем пару вариантов реализации этого класса.

Функция преобразования для вертикальной/горизонтальной шкалы

Есть линейные и логарифмические шкалы. Учитывая, что вертикальная шкала может быть сделана в одном формате, а горизонтальная — в другом, мы получаем четыре варианта графика:

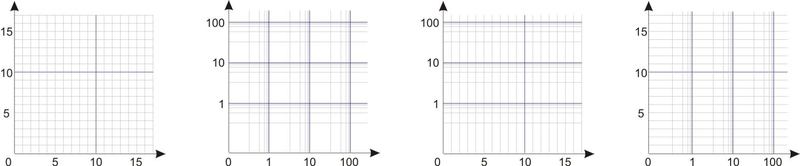
Вариант первый — обе шкалы линейные. Вариант второй — обе логарифмические. Варианты третий и четвертый — смешанные графики. Кстати, в моем случае именно смешанный случай в итоге и подошел, т. к. по горизонтали у меня потребовался логарифмический масштаб, по вертикали — линейный.

Следовательно, задачу отображения нужно решать отдельно для обеих осей.

Напомним, что при отображении на экран используется преобразование в координаты $(t,f(t))\Rightarrow(X,Y)$ , где $X=X(t)$ , $Y=Y(f(t))$ . Наша дальнейшая задача — построить эти функции для линейного и логарифмического случаев.

Что это за функции такие? На вход они получают координату в абстрактных (для компьютерной подпрограммы отображения на экран) координатах, на выход дают в экранных («экранные» координаты будут для разных операционных систем разными"). Для расчета им нужно знать следующее:

пределы абстрактных координат — те предельные значения аргумента и функции, что нас интересуют. Это будут $t_{min}$ , $t_{max}$ для горизонтальной оси и $f(t)_{min}$ , $f(t)_{max}$ для вертикальной. Не нужно допускать классическую ошибку: $f(t)_{min}=t_{min}$ , $f(t)_{max}=t_{max}$ ! В приведенном примере это проиллюстрировано;
пределы экранных координат — границы картинки, в которой рисуется график. Естественно, в текущих экранных координатах. На графике это $x_{min}$ , $x_{max}$ для горизонтальной оси и $y_{min}$ , $y_{max}$ для вертикальной;
шаг экранной координаты — текущий шаг пикселя $x_{step}$ , $y_{step}$ . В простом случае это будет единица. Но в Qt вертикальный ноль — это верх окна. Следовательно, $y_{step}=-1$ . А еще могут быть применены всякие трансформации, и шаг уже будет отнюдь не единичным.

Обратите внимание — для задачи преобразования не важно, вертикальная это ось или нет! Она (задача) оперирует граничными значения входного, выходного, а также шагом выходного параметров. Следовательно, задачу можно обобщить: необходимо преобразовать параметр $val$ на основе его пределов $val_{min}$ , $val_{max}$ в выходную величину $scr$ с учетом ее пределов $scr_{min}$ , $scr_{max}$ и шага $scr_{step}$ . Тут намеренно введены обозначения $val$ , $scr$ вместо привычных $x$ , $y$ , т. к. иначе будет путаница. Одно существенное дополнение: $val_{max}>val_{min}$ .

Базовый класс для преобразований шкал

Давайте сформулируем желаемую функциональность виртуального класса преобразований для шкалы, от которого будут унаследованы реализации шкал:

преобразований из экранных координат в абстрактные и наоборот — логично, ради этого мы его и делаем;
настройка преобразования — это тоже логично;
свойства — текущие свойства преобразования (минимальные/максимальные значения, шаг для разных значений);
информация по сетке — позиции для крупной и мелкой сетки, подписи под шкалой.

Реализация может выглядеть так:

class ScaleBase { public: 	// . преобразования 	virtual qreal scr (const qreal Val) const = 0;		// преобразование из исходных координат в экранные 	virtual qreal val (const qreal Scr) const = 0;		// преобразование из экранных координат в исходные  	// . массивы 	virtual const QVector<qreal> &scr_values (void) const = 0;		// массив исходных значений, соответствующих [экранной координате (относительно начала шкалы на экране)] 	int num_scr_values (void) const; 	virtual const QVector<int> &scr_min_grid (void) const = 0;		// массив смещений для мелкой сетки 	int num_scr_min_grid (void) const; 	virtual const QVector<int> &scr_maj_grid (void) const = 0;		// массив смещений для крупной сетки 	int num_scr_maj_grid (void) const; 	virtual const QVector<int> &scr_text_pos (void) const = 0;		// массив смещений для подписей под шкалой 	int num_scr_text_pos (void) const; 	virtual const QVector<QString> &scr_text_str (void) const = 0;	// массив текстов для подписей под шкалой 	int num_scr_text_str (void) const;  	// . свойства 	virtual qreal val_min (void) const = 0;		// возврат минимального значения исходной величины, отображаемой на экране 	virtual qreal val_max (void) const = 0;		// возврат максимального значения исходной величины, отображаемой на экране 	virtual qreal scr_min (void) const = 0;		// возврат минимального значения исходной величины 	virtual qreal scr_max (void) const = 0;		// возврат максимального значения исходной величины 	virtual bool is_specified (void) const = 0;	// преобразование определено  	// . настройка 	virtual void set_val_min (const qreal Val) = 0;		// установка минимального значения исходной величины, отображаемой на экране 	virtual void set_val_max (const qreal Val) = 0;		// установка максимального значения исходной величины, отображаемой на экране 	virtual void set_scr_min (const qreal Src) = 0;		// установка минимального значения экранной величины 	virtual void set_scr_max (const qreal Src) = 0;		// установка максимального значения экранной величины 	virtual void set_scr_point (const qreal Src) = 0;	// установка минимального экранного шага (пикселя)  	// . события 	void Resized (const qreal Size) = 0;		// изменился размер экрана  	// . перегруженные операторы 	operator bool (void) const					{ return is_specified (); }		// преобразование определено };	// class ScaleBase  int ScaleBase::num_scr_values (void) const { 	return scr_values().size(); } int ScaleBase::num_scr_min_grid (void) const { 	return scr_min_grid().size(); } int ScaleBase::num_scr_max_grid (void) const { 	return scr_max_grid().size(); } int ScaleBase::num_scr_text_str (void) const { 	return scr_text_str().size(); } int ScaleBase::num_scr_text_pos (void) const { 	return scr_text_pos().size(); } virtual qreal ScaleBase::scr_step (const int Num) const { 	Q_ASSERT_X (Num < num_scr_values (), "receiving step", (QString ("incorrect step index %1 for array size %2 is used"). arg (Num). arg (num_scr_values())).toAscii().constData()); 	return scr_values()[Num + 1] - scr_values()[Num]; }

Настройка шкалы производится функциями set_... (Val). Пересчет необходимых значений должен производится в этих же функциях. При изменении размера окна вызывается метод Resized (Size).

Для повышения производительности можно один раз рассчитать соответствие точки на экране и ее значение в исходных, абстрактных координатах. Этот массив возвращается методом scr_values () const. Далее, для построения крупной и мелкой сетки рассчитываются массивы (возвращают их, соответственно, функции scr_maj_grid () и scr_min_grid ()). Длина массива соответствует количеству оных линий, значение — смещению относительно начала шкалы на экране (т. е. индексу первого массива). Также заранее рассчитываются два массива — текст подписи к шкале (функция scr_text_str ()) и смещения этих подписей относительно начала (функция scr_text_pos ()).

Наконец, прямое преобразование — из абстрактных в экранные координаты — производится функцией scr (Val), обратное — функцией val (Scr).

Линейное преобразование

Давайте отдельно рассмотрим линейное преобразование для горизонтальной и вертикальной оси.

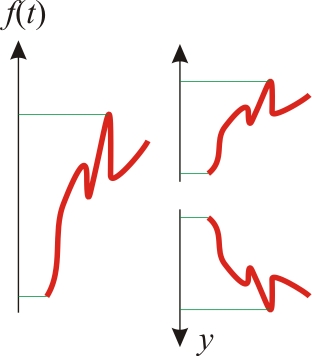
Мы имеем некоторую функцию — кривую в одном представлении. Для другого нам пришлось ее сузить и сместить вправо (окно на экране уменьшили и сдвинули вправо). Для другого представления нам пришлось сместить ее влево (окно сдвинули влево). Как это описывается математически? Достаточно просто: $y=f(k*t+b)$ . В первом случае, похоже, $0<k<1$ , во втором $b<0$ .

В другом случае нам пришлось сузить вертикальное представление кривой и сдвинуть вверх. А потом и вообще — перевернуть. Оба этих преобразования описываются как $y=k*f(t)+b$ . В первом случае $0<k<1$ , $b>0$ . Во втором случае $k=-1$ .

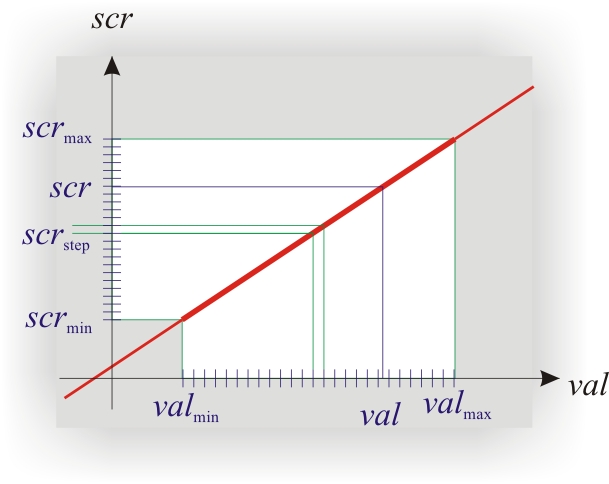
Оба преобразования имеют одно и то же математическое описание: $scr=k*val+b$ . В данном описании есть две константы, которые определяют преобразование — $k$ и $b$ . Первая определяет угол наклона, вторая — смещение относительно нуля.

Расчет этих констант достаточно прост — это решение системы двух уравнений:

$\left\{\begin{matrix}scr_{min}=k*val_{min}+b; \\scr_{max}=k*val_{max}+b; \end{matrix}\right. \Rightarrow \left\{\begin{matrix}k=\frac{scr_{min}-scr_{max}}{val_{min}-val_{max}}; \\b=scr_{max}-k*val_{max}; \end{matrix}\right.$ .

Еще важно уметь делать обратное преобразование — скажем, координаты указателя мыши перевести в абстрактные координаты. Также ничего сложного:

$val=\frac{scr-b}{k}$ .

Шаг $scr_{step}$ в данном случае для расчета не используется, но он потом нам пригодится в реализации на С++ для расчета смещения.

Как это будет использоваться на практике? Да все просто! Горизонтальное преобразование: $scr_{min}$ — граница картинки графика, соответствующая $val_{min}$ (как правило, слева), $scr_{max}$ — $val_{min}$ (как правило, справа), $scr_{step}$ — шаг вывода картинки по горизонтали. Вертикальное преобразование — аналогично, но по вертикали (у нас в Qt $scr_{min}$ будет нижней границей картинки, $scr_{max}$ — верхней, причем $scr_{min}>scr_{max}$ ).

Логарифмическое преобразование

А теперь окунемся туда, ради чего все это закрутилось:

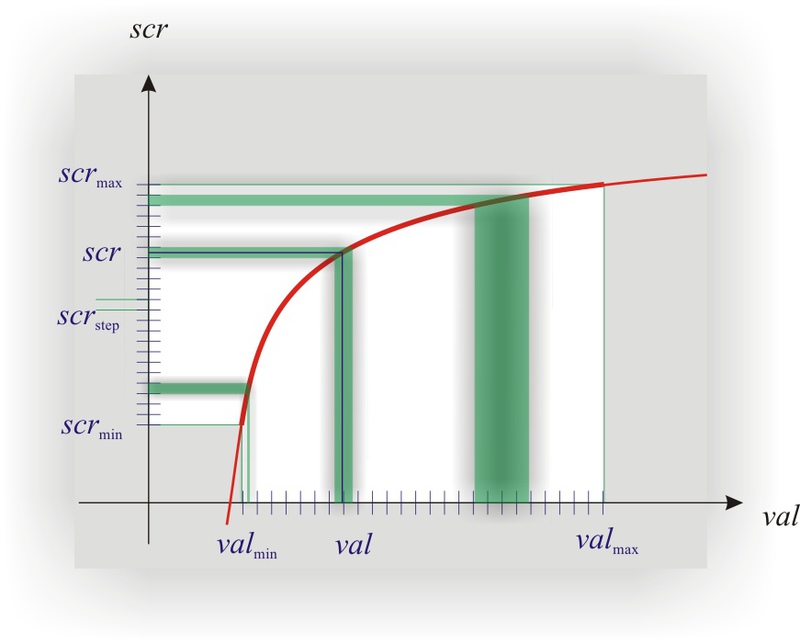
(на графике не логарифм нарисован, а что-то похожее на него. Сделано это специально, т. к. логарифм тут будет не очень нагляден)

Если $scr_{step}$ один и тот же на всей шкале, то $val_{step}$ будет везде разным! По какому закону он меняется? Правильно — по логарифмическому! Давайте первым делом научимся определять этот самый $val_{step}$ .

Всего точек у нас будет $num=\left | \frac{scr_{max}-scr_{min}}{scr_{step}} \right |+1$ (например, $scr_{min}=-1$ , $scr_{max}=1$ , $scr_{step}=1$ ; тогда у нас будет 3 точки). Этому соответствует диапазон входных значений $diap_{val}=val_{max}-val_{min}$ . Значению $scr_{0}=scr_{min}$ соответствует $val_{0}=val_{min}$ , $scr_{n}=scr_{max}$ соответствует $val_{n}=val_{max}$ . Последняя точка имеет индекс $n=num-1$ . Чему соответствует $scr_{i}$ ?

Для линейной шкалы $scr_{i}\equiv val_{min}+base*i$ , где $base$ определяется диапазоном входных значений. Тут можно поступить аналогично, только вместо умножения будет возведение в степень: $scr_i\equiv val_{min}+base^i$ (помним, что $0\leqslant i\leqslant n$ ). Есть один, правда, ньюанс: при $i=0$ у нас $base^i\neq 0$ , а должно бы. Это решается просто — вычтем единицу: $scr_i\equiv val_{min}+base^i-1$ . И тогда для нулевого случая все сходится. Как рассчитать $base$ в данном случае? Есть разные варианты. Я это предпочитаю сделать следующим образом.

Нам известно, что $scr_n\equiv val_{max}$ . В то же время мы теперь знаем, что $scr_n\equiv val_{min}+base^n-1$ . Получается уравнение: $val_{max}=val_{min}+base^n-1$ . Решим его относительно $base$ : $base^n=val_{max}-val_{min}+1;base=\sqrt[n]{val_{max}-val_{min}+1}$ . Вспомнив, чему равно $n$ и заменив корень возведением в степень, получим приемлемый для компьютера вид: $base=(val_{max}-val_{min}+1)^{\tfrac{1}{num-1}}$ (напоминаю, что $val_{max}>val_{min}$ ). Прекрасно, базовая величина получена!

Фактически, мы получили алгоритм преобразования из экранной координаты в абстрактную — обратная задача. Теперь режим прямую задачу — преобразование из абстрактной координаты в экранную. Задача решается несложно. Фактически, нужно найти $i$ , а для него несложно и $scr_i$ .

Для нахождения $i$ надо решить уравнение $val_{min}+base^i-1=val_i$ относительно $base^i$ : $base^i=val_i-val_{min}+1$ . Ну а дальше уже из свойств логарифма получим, что $i=\frac{\log (val_i-val_{min}+1)}{\log base}$ . Ну и далее, рассматривая экранные координаты как линию с наклоном, получим, что $scr_i=\frac{scr_{max}-scr_{min}}{n}*i+scr_{min}$ (для полной красоты надо еще $n$ заменить на $num-1$ ).