 Доброго времени суток, уважаемые читатели.
Доброго времени суток, уважаемые читатели. Многие из вас наверняка знают о том, что на протяжении нескольких лет NIST проводил конкурс среди хеш-функций с целью принятия нового стандарта SHA-3. И в этом году награда нашла своего героя. Новый стандарт был благополучно принят.
Ну а раз стандарт уже принят, самое время посмотреть что же он из себя представляет.
И тихим, субботним вечером, я
Прелюдия
В качестве нового стандарта была выбрана хеш-функция Keccack с переменной длиной выхода 224,256,384 и 512 бит. В основе Keccack лежит конструкция под названием Sponge(губка, та самая с верхней картинки).
Данную конструкцию можно представить следующим образом:
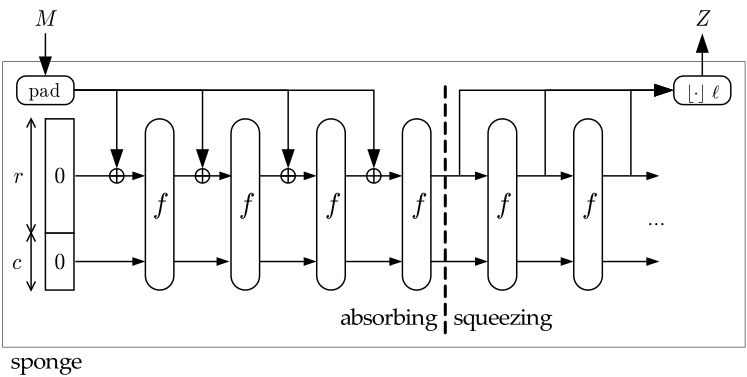
Как видно из рисунка схема состоит из двух этапов:
- Absorbing(впитывание). Исходное сообщение M подвергается многораундовым перестановкам f.
- Squeezing(отжатие). Вывод получившегося в результате перестановок значения Z.
Внимательный читатель наверняка заметил на рисунке буквы r и с. Не будем раньше времени раскрывать интригу, скажем только что варьируя значение этих переменных мы получим абсолютно разные хеш-функции. Так для SHA-512, в качестве этих значений нужно выбрать r=576, c=1024.
А поподробнее?
Итак, как я уже сказал выше, алгоритм Keccack основан на конструкции Sponge. Это означает, что для получения хеша Нам нужно проделать следующие незамысловатые действия:
- Взять исходное сообщение M и дополнить его до длины кратной r. Правила дополнения пленяют своей простотой. В виде формулы их можно изобразить следующим образом: M=M||0x01||0x00||..||0x00||0x80. Или говоря по-русски, к сообщению дописывается единичный байт, необходимое количество нулей и весь этот ансамбль завершает байт со значением 0x80.
- Затем для каждого блока Mi длиной r бит выполняем:
- Сложение по модулю 2 с первыми r-битами набора начальных состояний S. Перед началом работы функции все элементы S будут равны нулю.
- N раз применяем к полученным в результате данным функцию f. Набором начальных состояний S для блока Mi+1 будет результат последнего раунда блока Mi.
- После того как все блоки Mi закончатся взять итоговый результат и вернуть его в качестве хеш-значения.
Все равно ничего не понятно!
Ну а теперь вся подноготная алгоритма с блекждеком и шлюхами кодом и пояснениями.
Но сперва сорвем таки покровы с тайны и расскажем для чего нужны параметры r и c.
Для этого нужно сказать, что хеш-функция Keccack реализована таким образом, что функцию перестановки f, применяемую для каждого блока Mi, пользователь может выбирать самостоятельно из набора предопределенных функции b={f-25, f-50, f-100, f-200, f-400, f-800, f-1600}.
Для того чтобы в вашей реализации использовалась, скажем, функция f-800, необходимо выбрать такие r и c, чтобы выполнялось равенство r+c=800.
Кроме того, изменяя значения r и c, вы тем самым изменяете количество раундов вашей хеш-функции. Т.к. количество оных вычисляется по формуле n=12+2l, где 2l=(b/25). Так для b=1600, Количество раундов равно 24.
Однако хотя пользователь в праве выбирать для своей реализации любую из предложенных авторами функций, следует отметить что в качестве стандарта SHA-3 принята только функция Keccack-1600 и авторы всячески рекомендуют пользоваться только ею. Так в качестве основных значений для хешей разной длины авторы выбрали следующие параметры:
SHA-224: r=1156, c=448 (вернуть первые 28 байт результат)
SHA-256: r=1088, c=512 (вернуть первые 32 байт результат)
SHA-384: r=832, c=768 (вернуть первые 48 байт результат)
SHA-512: r=576, c=1024 (вернуть первые 64 байт результат)
А код-то где?
И после всех этих разъяснений можно уже перейти непосредственно к псевдокоду алгоритма.
Этап absorbing можно представить в виде следующей функции:
Keccak-f[b](A) { forall i in 0…nr-1 A = Round[b](A, RC[i]) return A } Здесь b это значение выбранной функции(по умолчанию 1600). А функция Round()-псевдослучайная перестановка, применяемая на каждом раунде. Количество раундов nr вычисляется из значений r и c.
Операции выполняемые на каждом раунде представляют из себя следующую функцию:
Round[b](A,RC) { θ step C[x] = A[x,0] xor A[x,1] xor A[x,2] xor A[x,3] xor A[x,4], forall x in 0…4 D[x] = C[x-1] xor rot(C[x+1],1), forall x in 0…4 A[x,y] = A[x,y] xor D[x], forall (x,y) in (0…4,0…4) ρ and π steps B[y,2*x+3*y] = rot(A[x,y], r[x,y]), forall (x,y) in (0…4,0…4) χ step A[x,y] = B[x,y] xor ((not B[x+1,y]) and B[x+2,y]), forall (x,y) in (0…4,0…4) ι step A[0,0] = A[0,0] xor RC return A } Она состоит из 4 шагов на каждом из которых над входящими данными производится ряд логических операций.
Здесь функция rot(X,n) обозначает циклический сдвиг элемента X на n позиций.
Массив r[] представляет собой предопределенный набор значений, в котором указывается на сколько необходимо сдвигать байты на каждом раунде. Значение всех элементов данного массива продемонстированы на таблице ниже:

Массив RC это набор констант, которые тоже являются предопределенными:

Сама же функция Keccack представляет из себя следующее:
Keccak[r,c](M) { Initialization and padding S[x,y] = 0, forall (x,y) in (0…4,0…4) P = M || 0x01 || 0x00 || … || 0x00 P = P xor (0x00 || … || 0x00 || 0x80) //Absorbing phase forall block Pi in P S[x,y] = S[x,y] xor Pi[x+5*y], forall (x,y) such that x+5*y < r/w S = Keccak-f[r+c](S) //Squeezing phase Z = empty string while output is requested Z = Z || S[x,y], forall (x,y) such that x+5*y < r/w S = Keccak-f[r+c](S) return Z } На этапе Absorbig производится вычисление хеш значения.
А на этапе Squeezing вывод результатов до тех пор пока не будет достигнута требуемая длина хеша.
public class Keccack { //константы рандов, всего их 24 //применяются на шаге ι private ulong[] RC ={0x0000000000000001, 0x0000000000008082, 0x800000000000808A, 0x8000000080008000, 0x000000000000808B, 0x0000000080000001, 0x8000000080008081, 0x8000000000008009, 0x000000000000008A, 0x0000000000000088, 0x0000000080008009, 0x000000008000000A, 0x000000008000808B, 0x800000000000008B, 0x8000000000008089, 0x8000000000008003, 0x8000000000008002, 0x8000000000000080, 0x000000000000800A, 0x800000008000000A, 0x8000000080008081, 0x8000000000008080, 0x0000000080000001, 0x8000000080008008}; //матрица смещений, применяется при каждом раунде на шаге θ private int[,] r = {{0, 36, 3, 41, 18} , {1, 44, 10, 45, 2} , {62, 6, 43, 15, 61} , {28, 55, 25, 21, 56} , {27, 20, 39, 8, 14} }; private int w, l, n; //в конструкторе устанавливаем параметры функции b=1600 public Keccack(int b) { w = b / 25; l = (Convert.ToInt32(Math.Log(w, 2))); n = 12 + 2 * l; } //циклический сдвиг переменной x на n бит private ulong rot(ulong x, int n) { n = n % w; return (((x << n) | (x >> (w - n)))); } private ulong[,] roundB(ulong[,] A, ulong RC) { ulong[] C = new ulong[5]; ulong[] D = new ulong[5]; ulong[,] B = new ulong[5, 5]; //шаг θ for (int i = 0; i < 5; i++) C[i] = A[i, 0] ^ A[i, 1] ^ A[i, 2] ^ A[i, 3] ^ A[i, 4]; for (int i = 0; i < 5; i++) D[i] = C[(i + 4) % 5] ^ rot(C[(i + 1) % 5], 1); for (int i = 0; i < 5; i++) for (int j = 0; j < 5; j++) A[i, j] = A[i, j] ^ D[i]; //шаги ρ и π for (int i = 0; i < 5; i++) for (int j = 0; j < 5; j++) B[j, (2 * i + 3 * j) % 5] = rot(A[i, j], r[i, j]); //шаг χ for (int i = 0; i < 5; i++) for (int j = 0; j < 5; j++) A[i, j] = B[i, j] ^ ((~B[(i + 1) % 5, j]) & B[(i + 2) % 5, j]); //шаг ι A[0, 0] = A[0, 0] ^ RC; return A; } private ulong[,] Keccackf(ulong[,] A) { for (int i = 0; i < n; i++) A = roundB(A, RC[i]); return A; } //функция дополняет 16-чную строку до размер r-байт и преобразует ее в матрицу 64-битных слов private ulong[][] padding(string M, int r) { int size = 0; //дополняем сообщение до длины кратной r M = M + "01"; do { M = M + "00"; } while (((M.Length / 2) * 8 % r) != ((r - 8))); M = M + "80"; //получаем из скольки блоков длиной b-бит состоит сообщение size = (((M.Length / 2) * 8) / r); //инициальзируем массив массивов 64-битных слов ulong[][] arrayM = new ulong[size][]; arrayM[0] = new ulong[1600 / w]; string temp = ""; int count = 0; int j = 0; int i = 0; //конвертируем строковое представление в массив 64-битных слов foreach (char ch in M) { if (j > (r/w-1)) { j = 0; i++; arrayM[i] = new ulong[1600 / w]; } count++; if ((count * 4 % w) == 0) { arrayM[i][j] = Convert.ToUInt64(M.Substring((count - w / 4), w / 4), 16); temp = ToReverseHexString(arrayM[i][j]); arrayM[i][j] = Convert.ToUInt64(temp, 16); j++; } } return arrayM; } private string ToReverseHexString(ulong S) { string temp = BitConverter.ToString(BitConverter.GetBytes(S).ToArray()).Replace("-", ""); return temp; } private string ToHexString(ulong S) { string temp = BitConverter.ToString(BitConverter.GetBytes(S).Reverse().ToArray()).Replace("-", ""); return temp; } // public string GetHash(string M, int r, int c, int d) { //Забиваем начальное значение матрицы S=0 ulong[,] S = new ulong[5, 5]; for (int i = 0; i < 5; i++) for (int j = 0; j < 5; j++) S[i, j] = 0; ulong[][] P = padding(M, r); //Сообщение P представляет собой массив элементов Pi, //каждый из которых в свою очередь является массивом 64-битных элементов foreach (ulong[] Pi in P) { for (int i = 0; i < 5; i++) for (int j = 0; j < 5; j++) if((i + j * 5)<(r/w)) S[i, j] = S[i, j] ^ Pi[i + j * 5]; Keccackf(S); } string Z = ""; //добавляем к возвращаемой строке значения, пока не достигнем нужной длины do { for (int i = 0; i < 5; i++) for (int j = 0; j < 5; j++) if ((5*i + j) < (r / w)) Z = Z + ToReverseHexString(S[j, i]); Keccackf(S); } while (Z.Length < d*2); return Z.Substring(0, d * 2); } }
Скачать исходники вы можете отсюда.
P.S. все материалы и иллюстрации для этой статьи были найдены на официальном сайте хеш-функции Keccack.
ссылка на оригинал статьи http://habrahabr.ru/post/159073/
Добавить комментарий