Введение в R-project

Во всем Хабре сыскалась лишь пара статей на вышеуказанную тему. А тема благодатная. Да и в минувшую среду как раз окончился курс "Introduction to Computational Finance and Financial Econometrics". По мотивам его пятой недели «Descriptive statistics» и появился этот пост. Причастившимся будет неинтересно, а желающих познакомиться с базовыми приемами анализа данных при помощи R  — прошу под хабракат.

Предварительные соглашения

О терминах

У автора из статистики был только семестр «тервера» N лет назад. Поэтому после сомнительно переведенных слов и их сочетаний будет указан исходный английский термин (курсивом в скобках). Специалисты, пожалуйста, шлите в личку более корректные варианты терминов. Спасибо.

Об установке

На установке ПО внимание не заостряется намеренно, в виду тривиальности. По крайней мере на Windows платформе все свелось к стандартному «далее -> далее ->… -> готово». Единственный требуемый для выполняемого в статье кода пакет PerformanceAnalytics устанавливается через меню «Пакеты / Установить пакет(ы)…», выбор ближайшего к вам зеркала, выбор нужного пакета из списка.

Набор данных

Хотелось избежать типичности: продажи, квартиры, рентабельность акций (simple returns), — сколько можно? Поэтому предметная область нашей выборки — вечна как в контексте Хабра, так и вне его контекста. Не так давно в блоге СамиЗнаетеКого был опубликован опрос «Какого размера у вас грудь?». Учитывая, что в него были включены два варианта ответа для отсева нерелевантной аудитории, есть некоторая уверенность в правдоподобии выборки. Для удобства результаты приведены и здесь:

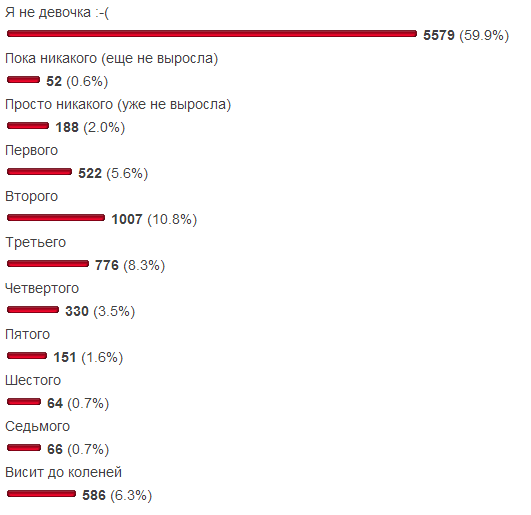
Цель

В рамках нашего мини-исследования сравним с нормальным распределением 2 набора данных:

• (НД1) варианты с третьего (уже не выросла) по девятый (шестой размер),
• (НД2) те же варианты, но к нулевому размеру добавим оптимисток (еще не выросла) и включим в данные седьмой размер.

Опытным статистикам очевидно, что изменениями второго варианта мы отдалим распределение от нормального. К финалу статьи у нас накопится достаточно сведений, чтобы обосновать это формально.

Ход исследования

Для начала поместим наши наборы данных в переменные:

data = c(rep(0, 184), rep(1, 510), rep(2, 996), rep(3, 763), rep(4, 327), rep(5, 147), rep(6, 60)) data_ol = c(data, rep(0, 51), rep(7, 65)) x.txt = "Размер груди" # и заодно сохраним повторяющееся наименование оси 

Функция c «склеивает» свои аргументы в единый вектор, функция rep(x, y) возвращает вектор из y значений x. Например, rep(0, 184) вернет вектор из ста восьмидесяти четырех нулей. В рекомендациях гугла и еще в нескольких источниках встречалось мнение, что символ равенства негоже использовать для присваивания, лучше — "<-". Знающие люди, пожалуйста, изложите в комментариях достаточно веские обоснования, чтобы писать 2 символа вместо одного. Лично для автора эта альтернатива отдает неудобством оператора ":=" из языка «Паскаль».

Теперь можно построить гистограммы:

par(mfrow=c(1, 2)) hist(data, breaks=0:7, right=F, col="seagreen", main="Гистограмма НД1", xlab=x.txt, ylab="Число респондентов") hist(data_ol, breaks=0:8, right=F, col="slateblue1", main="Гистограмма НД2", xlab=x.txt, ylab="Число респондентов") 

Первая строка нужна, чтобы гистограммы вывелись рядом. Без нее вторая гистограмма затрет первую. Вот, что получилось:

Напоминает результат опроса, верно? Верно, особенность нашего исследования в том, что данные сгенерированы на основе гистограммы. Но данный шаг не лишен смысла, т.к.

1. в ЖЖ нелинейный масштаб (скорее всего из-за количества голосов в первом варианте ответа);
2. обе гистограммы изображены в одном масштабе и ориетированы вертикально, что позволяет уже сейчас производить сравнение с плотностью вероятности (probability density function) нормального распределения.

Следующий шаг имеет мало смысла для столь дискретизированного набора данных, как у нас. Он приведен здесь только для ознакомления с функцией density, которая строит более «сглаженную» (читай, усредненную) гистограмму по выборке.

plot(density(data), type="l", col="seagreen", lwd=2, main="Сглаженная плотность НД1") plot(density(data_ol), type="l", col="slateblue1", lwd=2, main="Сглаженная плотность НД2") 

Результат:

Вычислим выборочные параметры распределений.

mu = mean(data) mu mu_ol = mean(data_ol) mu_ol var(data) var(data_ol) sig = sd(data) sig sig_ol = sd(data_ol) sig_ol library(PerformanceAnalytics) skewness(data) skewness(data_ol) kurtosis(data)# excess kurtosis (-3) kurtosis(data_ol) 

Результаты:

№ НД	Мат.ожидание	Дисперсия	Стандартное отклонение	Асимметрия (skewness)	Эксцесс (excess kurtosis)
1	2.408437	1.708542	1.307112	0.4124443	0.1001578
2	2.465034	2.17858	1.476001	0.7198767	0.7943986

Как видно из таблицы, изменения во втором наборе данных

• едва ли изменили в среднем ожидаемое значение,
• увеличили разброс случайной величины,
• почти в 2 раза увеличили искаженность распределения вправо (у плотности распределения удлиннился правый «хвост»),
• почти в 8 раз увеличили толщину «хвостов» (по сравнению с нормальным распределением).

Сравним эмпирические функции распределения (ЭФР) с функциями распределения (cumulative distribution function) соответствующих нормальных распределений (N(2.408437, (1.307112)²) и N(2.465034, (1.476001)²)).

n1 = length(data) plot(sort(data), (1:n1)/n1, type="S", col="seagreen", main="ЭФР НД1", xlab=x.txt, ylab="") x = seq(0, 6, by=0.25) lines(x, pnorm(x, mean=mu, sd=sig), type="l", col="orange", lwd=2) n2 = length(data_ol) plot(sort(data_ol), (1:n2)/n2, type="S", col="slateblue1", main="ЭФР НД2", xlab=x.txt, ylab="") x2 = seq(0, 7, by=0.25) lines(x2, pnorm(x2, mean=mu_ol, sd=sig_ol), type="l", col="orange", lwd=2) 

Вывод:

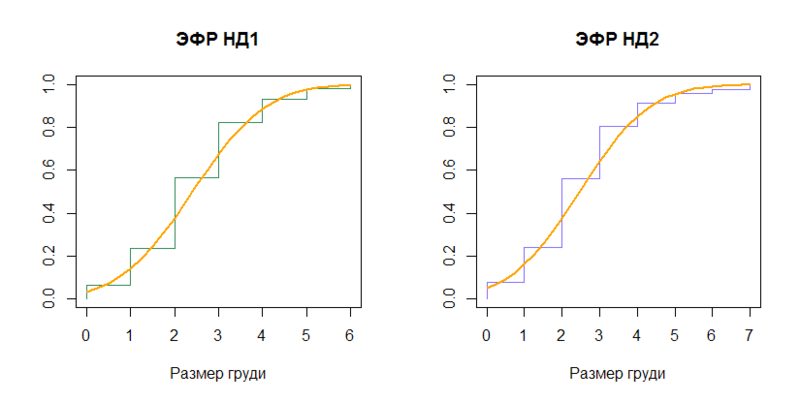
От функций распределения перейдем к квантилям (quantile), обратным функциям распределения.

quantile(data) quantile(data_ol) qnorm(p=c(0, .25, .5, .75, 1), mean=mu, sd=sig) qnorm(p=c(0, .25, .5, .75, 1), mean=mu_ol, sd=sig_ol) 

В нашем конкретном случае этап довольно скучный, т.к. выборки отличаются только сотым процентилем:

Распределение	q0	q.25	q.5	q.75	q1
НД1	0	2	2	3	6
N(2.408437, (1.307112)2)	-Inf	1.526803	2.408437	3.290070	Inf
НД2	0	2	2	3	7
N(2.465034, (1.476001)2)	-Inf	1.469486	2.465034	3.460582	Inf

И если НД1 квартилями походит на нормальное распределение хотя бы с округлением, то НД2 даже это не помогает.

Схема квантилей (normal Q-Q plot) для наших сильно дискретизированных выборок не сильно полезна. Упоминается, дабы осветить функцию qqnorm.

qqnorm((data-mu)/sig, col="seagreen") abline( 0, 1, col="orange", lwd=2) qqnorm((data_ol-mu_ol)/sig_ol, col="slateblue1") abline( 0, 1, col="orange", lwd=2) 

Результат выглядит не захватывающе, зато веселенько:

И завершает список наглядных выводов ящик с усами (boxplot).

boxplot(data, outchar=T, main="Ящик с усами НД1", ylab=x.txt) boxplot(data_ol, outchar=T, main="Ящик с усами НД2", ylab=x.txt) 

Графика:

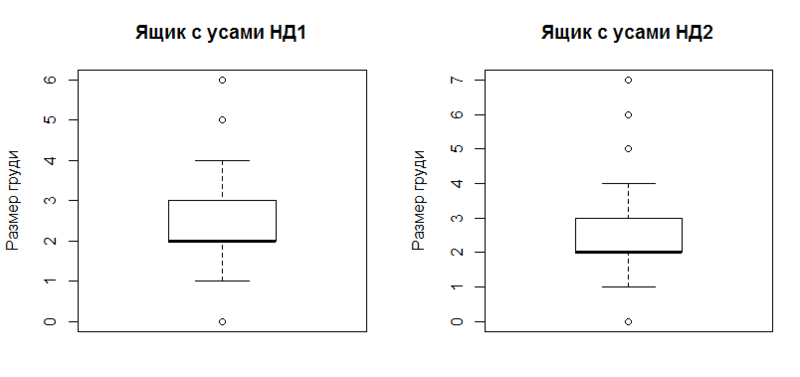
Построение наглядно отражает робастные характеристики выборки (устойчивые к наличию выбросов):

• первый и третий квартиль (верхняя и нижняя граница прямоугольника),
• второй квартиль (медиана, утолщенная горизонтальная линией),
• доверительный интервал (верхний и нижний «ус», все за этими пределами считается выбросами),
• собственно, выбросы (окружности за пределами «усов»).

Доверительный интервал в данном случае считается примерно как отступ от первого/третьего квартиля на 1,5 интерквартильного размаха. За подробностями — ?boxplot.

Заключение

НД1 отклоняется меньше НД2 от нормального распределения в виду:

• меньших значений асимметрии и эксцесса,
• меньшего различия квантилей распределения с выборочным ожиданием и выборочным стандартным отклонением в сравнении с квантилями выборки.

Дополнительная информация

Альтернативные вводные материалы в R (англ.):

• R Introduction, сопроводительные скрипты
• An Introduction to R
• R for Beginners

Вторая и третья ссылки — часть официальной документации. Если есть ссылки на дельные вводные статьи на великом и могучем, пишите — добавлю.

Основной целью статьи является привлечение внимания общественности к R как инструменту анализа. Если кто-либо из знающих людей представит более углубленный материал, буду искренне рад и с удовольствием ознакомлюсь.

Корректоры — в личку. Остальные — добро пожаловать в комментарии.
Спасибо всем за внимание.