 Это продолжение поста про оффлайн алгоритмы упаковки.
Это продолжение поста про оффлайн алгоритмы упаковки.
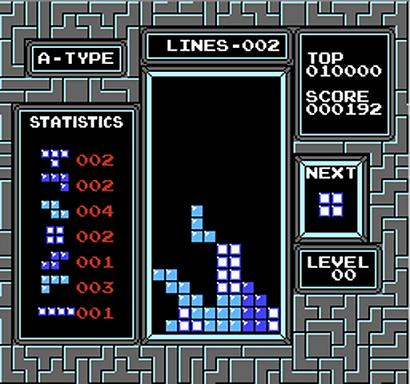
Суть задачи: имеем полубесконечную полосу — как в тетрисе, только без game over’а, и конечный набор прямоугольников. Данные о прямоугольниках поступают в режиме реального времени; каждый новый прямоугольник необходимо немедленно разместить и больше не двигать с места. Цель — минимизировать общую высоту упакованных прямоугольников.
Это online-вариация задачи об упаковке прямоугольников в полуограниченную полосу (2 Dimensional Strip Packing, 2DSP).
Чуть больше теоретических сведений можно найти в предыдущей статье, а пока, без лишних слов, перейдем к алгоритмам.
Для иллюстрации будет использоваться вот такая последовательность кирпичей:

(Спонсор исходных данных — random.org).
Будут описаны некоторые эвристические алгоритмы, общая идея которых состоит в том, чтобы предварительно разделить полосу на области, и размещать вновь поступающие прямоугольники в конкретной области по определенным критериям.
Level algorithms



Подход всех уровневых алгоритмов в том, что полоса разделяется на уровни, исходя из высоты имеющихся на данном этапе прямоугольников. Прямоугольники размещаются вдоль основания текущего уровня слева направо, пока это возможно; прямоугольник, который не поместился, упаковывается на следующий уровень. Высота каждого уровня определяется по самому высокому прямоугольнику в нем. Вот три варианта упаковки:
Next Fit Level — когда открывается следующий уровень, предыдущий «закрывается» и его больше не рассматриваем;
First Fit Level — на каждом шагу алгоритма просматривается каждый уровень, начиная с самого нижнего, и прямоугольник упаковывается на первый подходящий, на котором достаточно места;
Best Fit Level — на каждом шагу алгоритма просматриваются все уровни, и выбирается наиболее подходящий — тот, на котором после упаковки останется минимум места.
Все три алгоритма проиллюстрированы выше. На этом этапе несложно догадаться, какой где.
Input: The dimensions of the rectangles {w(Li); h(Li)} and the strip width W. Output: The height H and the entire packing. 1: level = 0; h(level + 1) = 0; H = 0; i = 0 2: while there is an unpacked rectangle do 3: i++ 4: if there is sufficient space on current level then 5: pack rectangle left justified 6: if h(level + 1) < h(Li) then 7: h(level + 1) = h(Li) 8: end if 9: else [there is insufficient space on current level] 10: open a new level and pack the rectangle 11: H += h(level + 1); level++ 12: end if 13: end while 14: print H and entire packing
First Fit Level
Input: The dimensions of the rectangles {w(Li); h(Li)} and the strip width W. Output: The height H and the entire packing. 1: level = 0; h(level + 1) = h(L1); H = h(L1); i = 1 2: while there is an unpacked rectangle do 3: i++; level = 0 4: search for the lowest level with sufficient space 5: if such a level exists then 6: pack rectangle left justified 7: if this is the top-most level and h(level) < h(Li) then 8: h(level) = h(Li) 9: end if 10: else [there is insufficient space in all existing levels] 11: create a new level above the top-most level 12: pack rectangle left justified 13: h(level) = h(Li); H += h(Li) 14: end if 15: end while 16: print H and entire packing
Best Fit Level
Input: The dimensions of the rectangles {w(Li); h(Li)} and the strip width W. Output: The height H and the entire packing. 1: level = 0; h(level + 1) = h(L1); H = h(L1); i = 0 2: while there is an unpacked rectangle do 3: i++; level = 0 4: search for lowest level with minimum residual horizontal space 5: if such a level exists then 6: pack rectangle left justified 7: else [such a level does not exist] 8: create a new level above the top-most level 9: pack rectangle left justified 10: h(level) = h(Li); H += h(Li) 11: end if 12: end while 13: print H and entire packing
Bi-Level Next Fit

Хитрая модификация Next Fit Level. Уровни создаются по два, на каждом из которых своя стратегия.
Нижний уровень (или все нечетные): первый пришедший прямоугольник упаковывается по левому краю, остальные — справа налево, пока достаточно места. Затем уровень закрывается и его высота определяется по самому высокому прямоугольнику в нем.
Верхний уровень (или все четные): если на нижнем уровне всего один прямоугольник, уровень упаковывается аналогично нижнему. Если два и больше, то первый прямоугольник упаковывается над более низким из двух прижатых к краям полосы, и также прижимается к краю полосы; все последующие упаковываются справа налево, независимо от того, где был упакован первый — слева или справа.
Звучит путано и не сразу понятно, к чему такие танцы с бубном. Единственное, что очевидно обеспечивает этот алгоритм — это более равномерное распределение прямоугольников по объему полосы, без перекоса к левому краю. Но мы еще вернемся к этой стратегии, когда будем рассматривать алгоритмы компрессии.
Input: The dimensions of the rectangles {w(Li); h(Li)} and the strip width W. Output: The height H and the entire packing. 1: level = 1; h(level) = 0; H = 0; i = 1 2: open a new bi-level 3: call 'pack on lower level' 4: print H and entire packing Procedure 'pack on lower level' 1: the first rectangle packed is left justified 2: subsequent rectangles that fit are right justified 3: if there is insufficient space then 4: h(level) is given by the height of tallest rectangle packed 5: call 'pack on upper level' 6: end if Procedure 'pack on the upper level' 1: if Li+1 is the first rectangle packed then 2: left justify on top of Li 3: else 4: if Li+2 is the first rectangle packed then 5: pack above min {h(Li); h(Li+1)} 6: justify according to min {h(Li); h(Li+1)} 7: else 8: if Li+j (j > 3) fits on the upper level then 9: left justify all other rectangles 10: else [rectangle does not fit] 11: H += h(lower) + h(upper); open new bi-level 12: end if 13: end if 14: end if
Shelf algorithms



Шельфовые алгоритмы не привязываются к точной высоте прямоугольников и после упаковки первого на уровне (шельфе) остается немного места на случай если следующий будет немного выше. Это «немного» регулируется параметром r ∈ (0;1). Высота шельфа определяется как rk, где rk+1 < h(Li) ≤ rk для некоторого целого k и высоты первого упаковываемого прямоугольника h(Li). Аналогично уровневым алгоритмам, применяются стратегии обхода шельфов Next Fit, First Fit и Best Fit. Оставленный на каждом шельфе «резерв» становится выгодным в двух последних случаях (сравните FFL и FFS, BFL и BFS). В примере p=0,7.
Input: The dimensions of the rectangles {w(Li); h(Li)} the parameter r and the strip width W. Output: The height H and the entire packing. 1: shelf = 1; w(shelf) = 0; h(shelf) = r^k for some integer k; i = 0; H = h(shelf) 2: while there is an unpacked rectangle do 3: i++; compute k 4: if there is sufficient space and r^(k+1) < h(Li) ≤ r^k then 5: pack rectangle to the right of the previously packed rectangle 6: else [there is insufficient space] 7: create a new shelf on top of the previous one and pack rectangle Li on the new shelf. 8: shelf++; H += r^k 9: end if 10: end while 11: print H and entire packing.
First Fit Shelf
Input: The dimensions of the rectangles {w(Li); h(Li)} the parameter r and the strip width W. Output: The height H and the entire packing. 1: shelf = 1; h(shelf) = r^k for some integer k; i = 0; H = h(shelf); shelfnum = 1 2: while there is an unpacked rectangle do 3: i++; compute k 4: search for lowest shelf of appropriate height with sufficient space 5: if such a shelf exists then 6: pack rectangle to the right of the previously packed rectangle 7: else [there is insufficient space in all shelves of appropriate height or such a shelf does not exist] 8: create a new shelf above the top-most shelf and pack rectangle Li on the new shelf. 9: shelf++; H += r^k; shelfnum++ 10: end if 11: end while 12: print H and entire packing.
Best Fit Shelf
Input: The dimensions of the rectangles {w(Li); h(Li)} the parameter r and the strip width W. Output: The height H and the entire packing. 1: shelf = 1; h(shelf) = r^k for some integer k; i = 0; H = h(shelf); shelfnum = 1 2: while there is an unpacked rectangle do 3: i++; compute k 4: search all shelves (starting with the bottom) for one with appropriate height and has minimum residual horizontal space. 5: if such a shelf exists then 6: pack rectangle to the right of the previously packed rectangle 7: else [there is insufficient space or there is no shelf of appropriate height] 8: create a new shelf above the top-most shelf and pack the rectangle Li on the new shelf. 9: shelf++; H += r^k; shelfnum++ 10: end if 11: end while 12: print H and entire packing.
Harmonic Shelf

Harmonic Shelf пакует на один уровень прямоугольники не только со схожей высотой, но и со схожей шириной. В результате получится больше уровней, но заполнены они будут плотнее. Вводится дополнительный параметр M для расчета допустимой ширины.
Общая ширина полосы, для простоты возьмем ее за единицу, делится на M интервалов I1..IM. Автор утверждает, что разумное значение M находится в [3; 12]. Ширина интервалов рассчитывается по формуле:
 ;
; 
Для каждого прямоугольника рассчитывается значение p. Параметр k для высоты рассчитывается аналогично шельфовым алгоритмам. Проверяются два условия: есть ли для прямоугольника место на каком-нибудь шельфе высотой rk и соответствует ли его p уже упакованным там. Если хотя бы одно не выполнено, для него создается свой шельф, с блекджеком и максимально комфортными условиями. В примере p=0,7, M=4.
Input: The dimensions of the rectangles {w(Li); h(Li)} the parameters M, r and the strip width W. Output: The height H and the entire packing. 1: shelf = 1; h(shelf) = r^k for some integer k; i = 0 2: while there is an unpacked rectangle do 3: i++; compute k such that r^(k+1) < h(Li) ≤ r^k 4: compute the value of p such that 1/(p+1) < w(Li) ≤ 1/p where 1 ≤ p < M 5: amongst shelves of height r^k find the one with packing rectangles whose width fits in the interval Ip 6: if there is insufficient space or no rectangle of height r^k then 7: a new shelf of appropriate height is created above the top-most shelf 8: shelf++ 9: end if 10: if rectangle Li is the first on the shelf then 11: h(shelf) = r^k; H += h(shelf) 12: end if 13: end while 14: print H and entire packing
AzarY

Для деления на уровни вводится некое пороговое значение 0 < Y < 1/2. Ширина прямоугольников масштабируется в соответствии с шириной полосы, которая принимается за единицу. Прямоугольники высотой 2j-1 < h(Li) ≤ 2j и шириной 2—x-1 < h(Li) ≤ 2-x упаковываются на один уровень. То есть уровень характеризуется парой (x, j) для некоторого целого j и натурального x.
Прямоугольники шириной не менее Y нарекаются буферными и пакуются каждый на отдельный уровень. То есть если попался такой прямоугольник, нужно срочно открывать новый уровень, высотой равный ему. Все остальные (не-буферные) пакуются на первый подходящий уровень. Подходящий — в смысле с такой же парой (x, j). Если вдруг места не хватило, не-буферный прямоугольник может стать первым в новом уровне, тогда высота этого уровня будет 2j.
Какая-то нездоровая иерархия, в общем.
В примере Y=0,4.
Input: The dimensions of the rectangles {w(Li); h(Li)} the parameter Y and the strip width W. Output: The height H and the entire packing. 1: h(level) = 0; w(level) = 0; level = 0 2: while there is an unpacked rectangle do 3: if w(Li) ≥ Y then 4: level++; w(level) = w(Li); h(level) = h(Li); H += h(level) 5: else [w(Li) < Y ] 6: compute x and j such that 2^(j-1) < h(Li) ≤ 2^j and 2^(-x-1) < w(Li) ≤ 2^(-x) 7: search for the lowest (x, j) level 8: if no (x, j) level is available or Li is blocked then 9: level++; h(level) = 2^j; H += h(level) 10: w(level) += w(Li) 11: else [(x, j) level is available and not blocked] 12: w(level) += w(Li) 13: end if 14: end if 15: end while 16: print H and entire packing
Compression algorithms



Компрессионные алгоритмы основаны на BiNFL и по сути представляют собой патчи к методу упаковки верхнего уровня.
Общее отличие — верхний уровень всегда упаковывается слева направо.
Compression Part Fit: Для каждого прямоугольника, упакованного на верхний уровень, проверяется, есть ли под ним место на нижнем уровне. Если можно сдвинуть его на нижний уровень так, что часть его останется на верхнем, он сдвигается (отсюда Part Fit — он частично может быть «вжат» в предыдущий уровень). Таким образом можно снизить общую высоту второго уровня. Больше на упаковку он никак кардинально не влияет. На первом рисунке видно прямоугольник, висящий между уровней — он и был сдвинут.
Compression Full Fit: Для каждого прямоугольника, упакованного на верхний уровень, проверяется, может ли он полностью сместиться вниз на предыдущий уровень. Собственно, если может, то и смещается. Это дает нам стратегическое преимущество: освободившееся таким образом место на уровне может быть использовано для следующего прямоугольника. К сожалению, второй рисунок не содержит такую ситуацию, но зато на нем можно увидеть двоих провалившихся.
Compression Combo: Да-да, это комбинация двух предыдущих и, соответственно, комбинация их плюсов. Третий рисунок иллюстрирует.
Input: The dimensions of the rectangles {w(Li); h(Li)} and the strip width W. Output: The height H and the entire packing. 1: i = 0; H = 0 2: open new bi-level 3: packing on lower level is similar to BiNFL; H += h(lowerlevel) 4: if there is insufficient space to pack a rectangle on the lower level then 5: call 'pack on the upper level' 6: end if 7: print H and entire packing Procedure 'pack on the upper level' 1: while there is an unpacked rectangle do 2: if i ≥ 3 and Li is the first rectangle packed then 3: justify according to the shorter of the left-most and right-most rectangles 4: slide rectangle downwards if there is sufficient space and go to 12 5: else 6: if i ≥ 3 and Li is the second rectangle packed then 7: right justify and go to 12 8: else [rectangle does not fit] 9: H += h(upperlevel); open new bi-level 10: end if 11: end if 12: end while
Compression Part Fit
Input: The dimensions of the rectangles {w(Li); h(Li)} and the strip width W. Output: The height H and the entire packing. 1: i = 0; H = 0 2: open a new bi-level 3: packing on lower level is similar to BiNFL; H += h(lowerlevel) 4: if there is insufficient space to pack a rectangle on the lower level then 5: call 'pack on the upper level' 6: end if 7: print H and entire packing Procedure 'pack on the upper level' 1: while there is an unpacked rectangle do 2: if h(Li) > VerticalSpace and w(Li) ≤ HorizontalSpace then 3: shift rectangle Li downwards; go to 11 4: else 5: if h(Li) ≤ VerticalSpace and W - w(level) ≥ w(Li) then 6: left justify; go to 11 7: else [rectangle does not fit] 8: H += h(upperlevel); open a new bi-level 9: end if 10: end if 11: end while
Compression Full Fit
Input: The dimensions of the rectangles {w(Li); h(Li)} and the strip width W. Output: The height H and the entire packing. 1: i = 0; H = 0 2: open a new bi-level 3: packing on lower level is similar to BiNFL; H += h(lowerlevel) 4: if there is insufficient space to pack a rectangle on the lower level then 5: call 'pack on the upper level' 6: end if 7: print H and entire packing Procedure 'pack on the upper level' 1: while there is an unpacked rectangle do 2: if h(Li) ≤ VerticalSpace and w(Li) ≤ HorizontalSpace then 3: slide rectangle Li downwards; go to 11 4: else 5: if h(Li) ≤ VerticalSpace and W - w(level) ≥ w(Li) then 6: left justify; go to 11 7: else [rectangle does not fit] 8: H += h(upperlevel); open new bi-level 9: end if 10: end if 11: end while
Compression Combo
Input: The dimensions of the rectangles {w(Li); h(Li)} and the strip width W. Output: The height H and the entire packing. 1: i = 0; H = 0 2: open a new bi-level 3: packing on lower level is similar to BiNFL; H += h(lowerlevel) 4: if there is insufficient space to pack a rectangle on the lower level then 5: call 'pack on the upper level' 6: end if 7: print H and entire packing Procedure 'pack on the upper level' 1: while there is an unpacked rectangle do 2: if w(Li) ≤ HorizontalSpace then 3: slide rectangle Li downwards; go to 11 4: else 5: if w(Li) > HorizontalSpace and W - w(level) ≥ w(Li) then 6: left justify, go to 11 7: else [rectangle does not fit] 8: H += h(upperlevel); open new bi-level 9: end if 10: end if 11: end while
Online fit

Более трудоемкий метод, чем предыдущие, но и более производительный. Основан на алгоритме Burke для оффлайн-варианта задачи. Некоторые аспекты я, пожалуй, нарисую.


В процессе упаковки могут образовываться пустые области (Empty Areas), которые алгоритм будет пытаться заполнить в первую очередь. Как они могут образоваться, видно на фото слева. Заметим, что для этого нужно хранить некое представление заполненности полосы.
После заполнения из пустой области может получиться две (а может и не получиться, you know).

 Также одним шагом упаковки могут быть созданы сразу несколько областей — пространство под прямоугольником анализируется по вертикали и делится по количеству «ступенек». На среднем фото еще раз показано разбиение пустой области на две после упаковки туда прямоугольника (кстати, мне кажется, в этом месте оптимальнее было бы разбить ее по горизонтали).
Также одним шагом упаковки могут быть созданы сразу несколько областей — пространство под прямоугольником анализируется по вертикали и делится по количеству «ступенек». На среднем фото еще раз показано разбиение пустой области на две после упаковки туда прямоугольника (кстати, мне кажется, в этом месте оптимальнее было бы разбить ее по горизонтали).
В общем, чем дальше в лес, тем больше пустот. На каждом шаге пристально рассматриваются стремительно мельчающие пустоты. Здесь мне видится еще одна оптимизация: можно ввести меру целесообразной площади и отбрасывать неугодные.
 Если ни одна пустая область не подходит, упаковка продолжается методом Burke. Я напомню. Строится карта высот для полосы, и прямоугольник примеривается в самую низкую на данный момент область. Если он туда не входит, низкое место «заполняется» до уровня ближайшей ступеньки, и поиск повторяется. Так потенциальное место может быть вытолкнуто на самый верх, и тогда возникает еще один вариант образования пустого пространства (см. справа).
Если ни одна пустая область не подходит, упаковка продолжается методом Burke. Я напомню. Строится карта высот для полосы, и прямоугольник примеривается в самую низкую на данный момент область. Если он туда не входит, низкое место «заполняется» до уровня ближайшей ступеньки, и поиск повторяется. Так потенциальное место может быть вытолкнуто на самый верх, и тогда возникает еще один вариант образования пустого пространства (см. справа).
Та же карта высот используется на каждом шаге для выявления пустых областей.
В общем-то, все уже сказано. Сперва пытаемся упаковать по пустым областям, затем в наиболее низкое место, и в последнюю очередь — сверху, вырожденный случай «самого низкого места».
Input: The dimensions of the rectangles {w(Li); h(Li)} and the strip width W. Output: The height H and the entire packing. 1: i = 0; H = 0 2: Create a linear array whose number of elements are equal to W 3: while there is an unpacked rectangle do 4: i++ 5: Search the list of empty areas for sufficient space to pack Li 6: if w(EmptyArea) ≥ w(Li) and h(EmptyArea) ≥ h(Li) then 7: pack rectangle in empty area 8: else 9: if rectangle does not fit in any of the empty areas then 10: search the linear array for available packing width 11: else [there is insufficient space in linear array] 12: pack rectangle on top left justified from the index leading to smaller space 13: end if 14: end if 15: end while 16: H = highest entry in the linear array 17: print H and entire packing
Послесловие
Чтобы развеять ощущение бесцельности происходящего, приведу один из классических, но вдохновляющих примеров применения алгоритмов двумерной упаковки в полуограниченную полосу. Это планировщик задач для многопроцессорной системы. В современном софте для кластеров используются более «взрослые» алгоритмы, но сама задача планирования сводится к 2DSP. В условиях работы кластеров поток поступающих задач представляет собой не что иное, как online данные для упаковки: размерность по горизонтали — требуемое количество ядер, по вертикали — время работы задачи. (Все как на заре технологий: встаешь в очередь к компьютеру и заранее предупреждаешь, сколько тебе нужно ресурсов и как долго будет крутиться твоя перфокарта). Планировщик должен выделить для задачи конкретные процессоры и определить момент запуска. В чистом виде, кстати, ни один алгоритм использовать нельзя, так как время капает, пока планировщик ждет задачу или думает над ее размещением. Дополнительно программисту могут связывать руки разные специфические условия: приоритет задач; возможность масштабирования задачи во время выполнения; хардварные задержки и самообслуживание системы, в том числе перераспределение с учетом отказавших ресурсов; сопоставление характера коммуникаций внутри задачи с архитектурой кластера, etc.
Любой алгоритм прекрасен в своей математической строгости, пока не начнешь прикладывать его к реальной жизни.
И напоследок — сравнительная характеристика алгоритмов в приятном обезличенном виде. Здесь приведено отношение оптимальной высоты упаковки (сумма площадей прямоугольников, деленная на ширину полосы) к полученной.
| NFL | FFL | BFL | BiNFL | NFS | FFS | BFS | HS | AzarY | CPF | CFF | CC | OF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,56 | 0,63 | 0,75 | 0,56 | 0,45 | 0,57 | 0,57 | 0,37 | 0,44 | 0,60 | 0,59 | 0,63 | 0,72 |
Код (Qt):
Алгоритмы packager.h packager.cpp
Гуй window.h window.cpp renderarea.h renderarea.cpp main.cpp
ссылка на оригинал статьи http://habrahabr.ru/post/160869/
Добавить комментарий