Зависимость прозрачности от ориентации поверхности

На днях, вертя в руках пластиковый стаканчик, я обратил внимание на то, что видимая прозрачность пластика за висит от угла, под которым смотришь на поверхность — если смотреть перпендикулярно поверхности, то задний фон отчетливо виден, а если смотреть вдоль поверхности, то материал становится практически непрозрачным. Это явление меня заинтересовало, и я решил построить математическую модель.

Сказано — сделано. Под катом вывод формулы, код фрагментного шейдера и небольшое демо.

Будем считать что материал оптический однородный — его оптические свойства не зависят от направления. Тогда изменение прозрачности обуславливается разной длиной пути светового луча в толще материала.

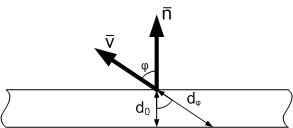
, где — единичный вектор нормали к поверхности, — единичный вектор направления на наблюдателя.

Пусть видимая прозрачность материала определяется коэффициентом непрозрачности, который определяет смешивание цвета материала с цветом фона следующим образом:

Давайте посмотрим, как значение зависит от толщины материала. Для этого разобьем слой материла c толщиной и коэффициентом непрозрачности на слоев одинаковой толщины , каждый с коэффициентом непрозрачности . Пусть — цвет фона, — цвет материала, а — цвет на выходе каждого слоя.

Но также , а следовательно:

Т.е. с увеличением толщины видимая прозрачность материала убывает экспоненциально.

Пусть толщина , тогда:

Итак, искомая формула:

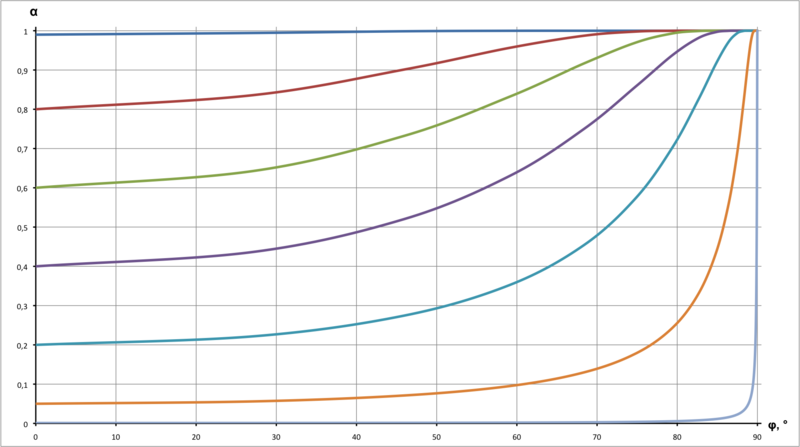
Ниже приведен код фрагментного шейдера, который реализует эту формулу:

varying vec4 v_color; varying vec3 v_normal; varying vec3 v_eye;  void main(void) {     // Вектора нормали и направления на наблюдателя не нормализированы     float cosPhi = dot(v_normal, v_eye) / sqrt( dot(v_normal, v_normal) * dot(v_eye, v_eye) );     // Косинус берется по модулю, на случай если наблюдатель находится сзади поверхности     // Чтобы избежать деления на нуль, значение косинуса принудительно ограничено снизу     // 0.999 ^ 10000 = 4.5173346E-5     float alpha = 1.0 - pow(1.0 - v_color.a, 1.0 / max(abs(cosPhi), 0.00001));     gl_FragColor = vec4(vec3(v_color), alpha); }; 

В результате получается вот что:

Исходный код демонстрационного приложения доступен на bitbucket.org