Затухание и взрывной рост изменения весов
Для начала давайте взглянем на одинаковые с виду графики.
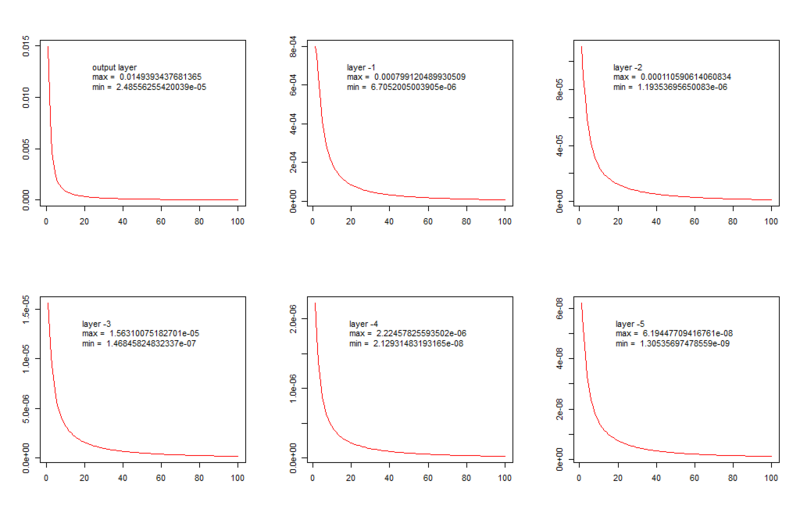
На них изображена зависимость среднего изменения веса в слое (ось ординат) от пройденных эпох обучения (ось абсцисс). Обучалась сеть следующей структуры: шесть слоев, 5 скрытых по 100 нейронов и выходной из 26 нейронов (количество классов, или букв в английском алфавите).
| input dimension = 841 | layer -5 | layer -4 | layer -3 | layer -2 | layer -1 | output |
| 100 neurons | 100 neurons | 100 neurons | 100 neurons | 100 neurons | 26 neurons |
Как видим, динамика в принципе одинаковая, но минимальное среднее изменение весов в выходном слое такого же порядка, как максимальное — в третьем скрытом слое, а в дальних слоях — еще меньше. В данном случае мы наблюдаем затухание градиента, а противоположная картина называется «взрывной рост градиента» (в английской литературе это называется «vanishing and exploding gradients»), чтобы увидеть этот эффект, достаточно инициализировать веса большими значениями. Для того, чтобы понять математику, советую обратиться, например, к этим статьям:
- Understanding the difficulty of training deep feedforward neural networks
- Understanding the exploding gradient problem
А мы сейчас попробуем разобраться на пальцах в причинах этого явления, опираясь на то, как это было преподнесено в курсе по нейросетям на курсере. Итак, что из себя представляет прямой проход сигнала по нейросети? На каждом слое вычисляется линейная комбинация входного сигнала слоя и весов каждого нейрона, в результате получается скаляр в каждом нейроне, а затем вычисляется значение функции активации. Как правило, функция активации, помимо необходимой нам нелинейности, помогает ограничить выходные значения нейронов, но мы рассмотрим лишь функцию активации общего вида. Таким образом, на выходе получается вектор, каждая компонента которого находится в заранее известных пределах.
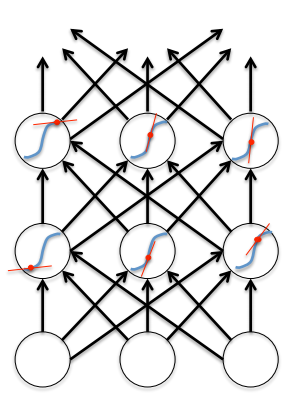
Теперь посмотрим на обратный проход. Градиенты на выходном слое легко вычисляются и получаются существенные изменения весов нейронов выходного слоя. Для любого скрытого слоя вспомним формулу вычисления градиента:
Если заменить выражение dE/dz, где участвует k, дельтой,
мы увидим, что обратный проход очень похож на прямой, но он полностью линеен, со всеми вытекающими последствиями. Дельта называется локальным градиентом/ошибкой нейрона. При обратном проходе дельты можно интерпретировать как выходы (в другую сторону) соответствующих нейронов. Значение градиента веса нейрона более глубокого слоя пропорционально значению производной функции активации в точке, полученной на прямом проходе. Вспомним геометрическое определение производной в точке:

x0 вычисляется и фиксируется при прямом проходе. Это красные линии на картинке выше. И получается, что линейная комбинация весов и локальных градиентов нейронов умножается на это значение, которое является тангенсом угла наклона касательной в точке x0, а область значений тангенса, как известно, лежит в интервале от минус бесконечности до плюс бесконечности.

Обратный проход для одного нейрона скрытого слоя выглядит следующим образом:

Что мы имеем в итоге:
- взрывной рост может случиться если веса слишком большие, или значение производной в точке слишком велико
- затухание происходит если значение весов или производной в точке очень мало
Как правило, неглубокие сети не страдают от этого из-за малого количества слоев, так как эффект не успевает аккумулироваться при обратном проходе (пример аккумуляции рассмотрим в следующем разделе).
Если же в качестве функции активации используется сигмоид
с производной следующего вида:
то при α = 1 мы легко можем убедиться, что максимальное значение, которого достигает производная, равно 0.25 в точке x = 0.5, а минимальное — 0 в точках x = 0 и x = 1 (на интервале от 0 до 1, области значений логистической функции):
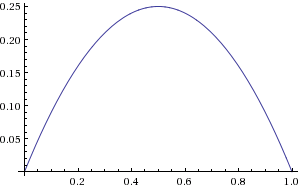
Следовательно, для сетей с логистической функцией активации взрывной рост и затухание в большей степени зависит от значения весов, хотя существует перманентное затухание из-за того, что в лучшем случае значение тангенса угла наклона касательной будет всего 0.25, а эти значения, как мы увидим в следующем разделе, от слоя к слою перемножаются:
- при очень малых значениях весов происходит затухание
- при достаточно крупных весах — рост
Простой пример
Для иллюстрации вышесказанного рассмотрим пример.

Дана простая сеть, минимизирующая квадрат Евклидова расстояния, с логистической функцией активации, найдем градиенты весов при входном образе x = 1 и целевом t = 0.5.
После прямого прохода получаем выходные значения каждого нейрона: 0.731058578630005, 0.188143725087062, 0.407022630083087, 0.307029145835665, 0.576159944190332. Обозначим их за y1, …, y5.
Как видим, происходит затухание градиента. По ходу вычисления заметно, что аккумуляция происходит за счет перемножения весов и значений производных текущего слоя и всех последующих. Хотя начальные значения далеко не маленькие, по сравнению с тем как веса инициализируются на практике, но и этих значений недостаточно, чтобы подавить перманентное затухание от тангенсов угла наклона касательной.
Предобучение
Прежде чем говорить о предложенном Джефри Хинтоном способе, стоит сразу же заметить, что на сегодняшний день не существует формального математического доказательства того, что предварительная тонкая настройка весов гарантирует улучшение качества работы сети. Итак, Хинтон предложил использовать ограниченные машины Больцмана для предварительной тонкой настройки весов. Как и в посте про RBM, мы сейчас будем говорить только о бинарных входных образах, хотя эта модель расширяется и на входные образы, состоящие из действительных чисел.
Предположим, у нас есть сеть прямого распространения следующей структуры: x1 -> x2 -> ... -> xn, где каждый xi — это количество нейронов в слое, xn — выходной слой. Обозначим за x0 размерность входного образа, который подается на вход, т.е. на слой x1. Так же у нас есть массив данных для обучения, данные (обозначим D0) — это пары вида «вход, ожидаемый выход», и мы хотим обучить сеть, используя алгоритм обратного распространения ошибки. Но перед этим осуществим тонкую инициализацию весов, для этого:
- Последовательно обучим по одной RBM для каждой последовательной пары слоев, включая фиктивный слой x0, в итоге получим ровно n штук RBM. Для начала берется первая пара
x0 <-> x1, она обучается на множестве входных образов из D0 (это обучение без учителя). Затем для каждого входного образа из D0 делается вывод вероятностей скрытого слоя и сэмплинг, получаем множество бинарных векторов D1. Затем с использованием D1 обучается параx1 <-> x2. И так далее доx{n-1} <-> xn. - Разбираем каждую RBM, и берем вторые слои с их же весами.
- Из выбранных вторых слоев каждой RBM составляем исходную сеть
x1 -> x2 -> ... -> xn.
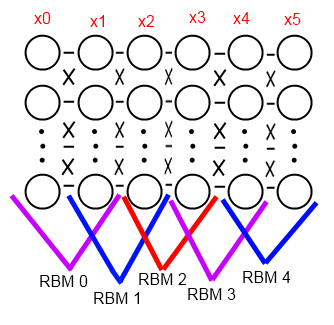
Такую сеть назвали Deep Belief Networks.
Как я уже сказал, эффективность этого способа не доказана, как и вообще эффективность какой-либо тонкой инициализации, но факт остается фактом — это работает. Объяснение этому эффекту можно дать следующее: при обучении самой первой RBM мы создаем модель, которая по видимым состояниям генерирует некоторые скрытые признаки, то есть мы сразу помещаем веса в некоторый минимум, необходимый для вычисления этих признаков; с каждым последующим слоем вычисляются признаки признаков, а веса всегда помещаются в состояние, достаточное для вычисления этих иерархических признаков; когда дело доходит до обучения с учителем, по сути, эффективно обучаться будут только 2-3 слоя от выхода, на основании тех гиперпризнаков, что были вычислены раньше, а те, в свою очередь, будут незначительно меняться в угоду задаче. Отсюда можно предположить, что не обязательно таким образом инициализировать все слои, а выходной и возможно 1-2 скрытых, можно инициализировать обычно, например, выбирая числа из нормального распределения с центром в 0 и дисперсией 0.01.
Исходные данные
Важную роль в этом посте играют эксперименты, так что следует сразу оговориться о множествах, используемых для обучения и тестирования моделей. Я сгенерировал несколько небольших и простых в обобщении множеств, чтобы на обучение сетей тратилось не более 30 минут.
- Обучающее множество состоит из изображений больших печатных букв английского алфавита трех шрифтов (Arial, Courier и Times как представители шрифтов разной породы) размером 29 на 29 пикселей, и их же изображений с некоторыми случайными шумами
- Кросс-валидационное множество состоит из того же набора шрифтов, плюс Tahoma и чуть больше шумов
- Тестовое множество состоит из того же набора данных, что и кросс-валидационное, отличается лишь фактором случайности при генерации шумов
Во всех опытах обучение будет останавливаться при выполнении следующего условия (как обучение сетей прямого распространения, так и машин Больцмана). Введем обозначения:
— это ошибка кросс-валидации текущей эпохи
— это ошибка кросс-валидации на прошлой эпохе
— это минимальная ошибка кросс-валидации, достигнутая от начала процесса обучения, до текущей эпохи
- k — параметр остановки при росте ошибки кросс-валидации, из интервала (0, 1)
Итак, процесс обучения будет прерван, если выполнено следующее условие:
т.е. если увеличение ошибки кросс-валидации больше, чем некоторый процент от минимальной ошибки, то происходит остановка.
В сетях прямого распространения выходным слоем будет softmax слой, а вся сеть обучается на минимизации перекрестной энтропии, соответственно, значение ошибок вычисляется тем же способом. А ограниченные машины Больцмана в качестве меры ошибки будут использовать расстояние Хэмминга между бинарным входным образом и бинарным восстановленным образом.
Эксперименты
Для начала посмотрим, какой результат даст нам сеть с одним скрытым слоем из 100 нейронов, т.е. структура ее будет 100 -> 26. Каждый процесс обучения проиллюстрируем графиком с ошибкой обучения и кросс-валидации.
Параметры обучения:
- LearningRate = 0.001
- BatchSize = full batch
- RegularizationFactor = 0
- Momentum = 0.9
- NeuronLocalGainLimit: Limit = [0.1, 10]; Bonus = 0.05; Penalty = 0.95
- CrossValidationStopFactor is 0.05

Результат на тестовом множестве, обучение заняло около 35 секунд:
Error: 1.39354424678178
Wins: 231 of 312, 74.03%
Если предобученная сеть покажет результат ниже этого, то это будет очень печально -). Предобучать мы будем сеть из 5 слоев следующей структуры: 100 -> 300 -> 100 -> 50 -> 26. Но для начала давайте посмотрим, как выглядит процесс обучения и результат, если обучить такую сеть без предобучения.
Параметры обучения:
- LearningRate = 0.001
- BatchSize = full batch
- RegularizationFactor = 0.1
- MaxEpoches = 2000
- MinError = 0.1
- Momentum = 0
- NeuronLocalGainLimit: not setted
- CrossValidationStopFactor is 0.001
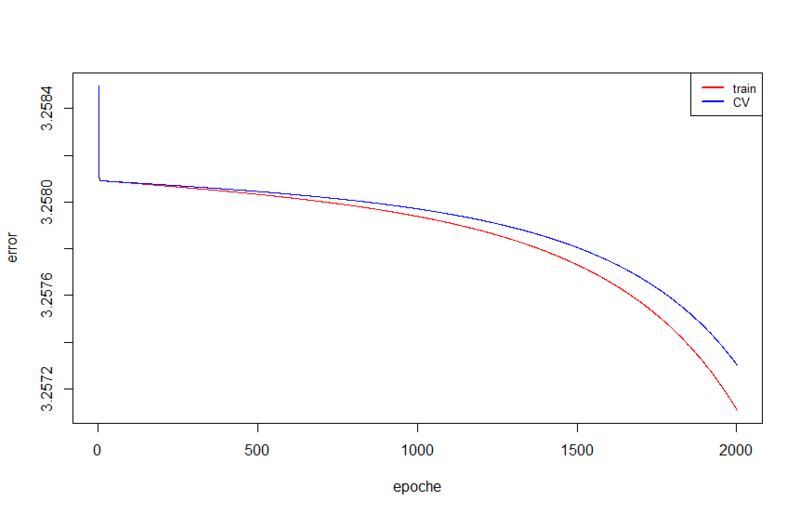
Результаты на тестовом множестве ничтожны, около 3 попаданий из 312. Обучение заняло 4300 секунд, это почти час двадцать (обучение было прервано на 2000 эпохе, хотя могло бы и продолжаться дальше). За 2000 эпох было достигнуто значение ошибки 3.25710954400557, в то время как в предыдущем тесте уже на второй эпохе было 3.2363407570674, а на последней 0.114535596947578.
А теперь давайте обучим RBM’ы для каждой последовательной пары. Для начала это будет 841 <-> 100 со следующими параметрами:
- LearningRate = 0.001
- BatchSize = 10
- Momentum = 0.9
- NeuronLocalGainLimit: Limit = [0.001, 1000]; Bonus = 0.0005; Penalty = 0.9995
- GibbsSamplingChainLength = 35
- UseBiases = True
- CrossValidationStopFactor is 0.5
- MinErrorChange = 0.0000001
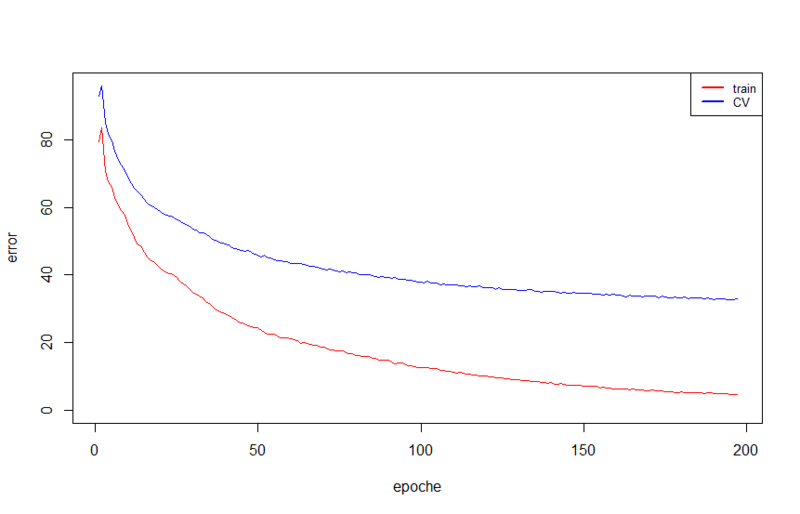
Обучение заняло 1274 секунды. Первую пару легко визуализировать, как это делалось в предыдущем посте. Получаются следующие шаблоны:

Увеличим немного:

Затем обучаем вторую пару 100 <-> 300, заняло 2095 секунд:
- LearningRate = 0.001
- BatchSize = 10
- Momentum = 0.9
- NeuronLocalGainLimit: Limit = [0.001, 1000]; Bonus = 0.0005; Penalty = 0.9995
- GibbsSamplingChainLength = 35
- UseBiases = True
- CrossValidationStopFactor is 0.1

Обучаем третью пару 300 <-> 100, заняло 1300 секунд:
- LearningRate = 0.001
- BatchSize = 10
- Momentum = 0.9
- NeuronLocalGainLimit: Limit = [0.001, 1000]; Bonus = 0.0005; Penalty = 0.9995
- GibbsSamplingChainLength = 35
- UseBiases = True
- CrossValidationStopFactor is 0.1

Веса выходного слоя и первого скрытого мы не трогаем и инициализируем случайными значениями из нормального распределения с центром 0 и дисперсией 0.01. Теперь складываем все слои в одну сеть прямого распространения и обучаем со следующими параметрами:
- LearningRate = 0.001
- BatchSize = full batch
- RegularizationFactor = 0
- Momentum = 0.9
- NeuronLocalGainLimit: Limit = [0.01, 100]; Bonus = 0.005; Penalty = 0.995
- CrossValidationStopFactor is 0.01

Результат на тестовом множестве, при том что обучение заняло всего 17 эпох или 36 секунд:
Error: 1.40156176438071
Wins: 267 of 312, 85.57%
Прирост качества составил почти 11% по сравнению с сетью с одним скрытым слоем. Я, честно говоря, ожидал большего, но тут уже дело в сложности данных. Как показали опыты и подтвердили прочитанные статьи, чем более сложный и большой массив данных у нас есть, тем больший прирост качества будет получен.
Заключение
Предобучение, очевидно, эффективный способ -) Возможно, какой-нибудь математический гений докажет его эффективность в теории, а не только на практике, как это есть сейчас.
Предположим, есть задача распознать капчи. У нас скачано 100 000 картинок, из них распознано вручную всего 10 000. Мы бы хотели обучить нейросеть, но нам жалко не использовать оставшиеся 90 000 тысяч картинок. Тут нам на помощь приходят RBM. Используя массив из 100 000 картинок, мы обучаем deep belief network, а затем на множестве из 10 000 распознанных вручную картинок мы обучаем глубокую сеть. Profit!
Ссылки
- Learning Internal Representations by Error Propagation
- Understanding the difficulty of training deep feedforward neural networks
- Understanding the exploding gradient problem
- Deep Boltzmann Machines
- A Practical Guide to Training Restricted Boltzmann Machines
- Deep Belief Networks
Спасибо юзеру OTHbIHE за помощь в редактировании статьи!
ссылка на оригинал статьи http://habrahabr.ru/post/163819/
Добавить комментарий