Вычислительная математика на Python — нахождение корней

В середине первого семестра я познакомился с одним довольно мощным математическим инструментом — Методом Ньютона, позволяющим при удачно выбранном начальном приближении довольно быстро вычислить корни почти любого многочлена.

Если вы знакомы с понятием производной, применение этого метода не окажется трудной задачей.
Формула выглядит следующим образом:


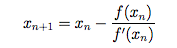
Xn означает начальное приближение, Xn+1 — следующее значение. Когда Xn+1 вычислено, и мы хотим получить более точный корень — подставляем Xn+1 в качестве начального приблежения.
То есть, по формуле, вычитаем из Xn дробь, в числителе — исходный многочлен, в знаменателе первая производная, в значение X везде подставляем Xn. Эту процедуру можно повторять бесконечно часто, разумеется результат будет становится бесконечно точнее.

Итак, для примера, выберем очень простой многочлен:

И в качестве начального приблежения возьмем -2 и выполним два цикла:

Разумеется, чем больше шагов, тем точнее результат.
Все это и навело меня на мысль написания кода на языке Python, выполняющий эту рутину.
Для начала, решил приступить к самой (как я сначала наивно полагал) сложной части, написав код, вычисляющий производную функции:

result = "" def der(p):     p = p + "a"     negative = 0     sign = p[0]     digits = "123456789"     x = p.find("x")     if p[x+1] == "^":         if p[x+3] in digits:             j = x + 2             while p[j] in digits:                 j = j + 1             exp = int(p[x+2:j])         else:             exp = int(p[x+2])     else:         exp = 1     p = "a"+p     x = p.find("x")          if p[x-1] in digits:         i = x-1         while p[i] in digits:             i = i - 1         number = int(p[i+1:x])     else:         number = 1     new_exp = exp-1     new_number = exp * number     if new_exp != 0:         if new_exp == 1:             new_exp_o = ""             circumflex = ""         else:             new_exp_o = new_exp             circumflex = "^"         if new_number == 1:             new_number_o = ""         else:             new_number_o = str(new_number)         a = new_number_o+"x" + circumflex + str(new_exp_o)         global result         if result == "":             result = a         else:             result = result + sign + a     else:         if sign == "+":             sign = ""         if x!=-1:             result = result + sign + str(new_number) def init(p):     p = p + "+"     t = ""     pol = []     c = 0     sign = ""     if p[0] != "-":         p = "+" + p          for j in range(len(p)):         if p[j] == "+" and j != 0:             pol.append(t)             sign = "+"             t = ""             if pol:                 pol         elif p[j] == "-" and j != 0:             pol.append(t)             sign = "-"             t = ""         else:             if sign != "":                 t = sign + t                 sign = ""             t = t + p[j]     for i in pol:         der(i)          if t!= "":         pol.append(t) p = raw_input("Ввести полином:") init(p) 

Разумеется, этот алгоритм несовершенен, не спорю, большинство читателей в состоянии написать код получше, но для моих целей он вполне подошел.

Осталось лишь написать код для самого алгоритма, использующий уже имеющую производную.

x0 = -2.0 #начальное приближение xnew = x0 for i in range(5):     xold = xnew     xnew = xold - (xold**3 - 2*xold + 3)/(3*xold**2 - 4)     print xnew 

Вот именно здесь я столкнулся с проблемой — исходный многочлен записывается в переменную «p» виде текста, также как и производная «a». Отсутствие программерского опыта дало о себе знаеть. Все мои попытки придумать решения пока вставали в тупик, но что-то мне подсказывает, что и это вполне посильная задача. Нынешний код делает тоже самое что и я сделал в тетради.

Буду рад если кто-нибудь придумает как реализовать этот алгоритм и найдет решение.