Многорукие бандиты: модель dynamic Gamma-Poisson

В прошлый раз мы рассмотрели общую постановку задачи о многоруких бандитах, обсудили, зачем это может быть нужно, и привели один очень простой, но эффективный алгоритм. Сегодня я расскажу о ещё одной модели, которая эффективна в ситуациях, когда ожидаемые доходы от бандитов меняются со временем, да и само число и состав «ручек» может меняться – о динамической гамма-пуассоновской модели.

Эта модель относится к так называемым онлайн-моделям рекомендаций. Постановка задачи здесь отличается от оффлайн-моделей (к которым относятся основные методы коллаборативной фильтрации – метод ближайших соседей, SVD и их варианты и так далее) тем, что главная цель онлайн-рекомендаций – как можно быстрее «поймать» изменения популярности тех или иных продуктов. Поскольку, как правило, данных недостаточно, чтобы такие изменения можно было отслеживать методами коллаборативной фильтрации, онлайн-методы обычно объединяют данные о рейтингах всех пользователей, не занимаясь персонализованными рекомендациями. Более того, часто возникают ситуации, когда система не может дать разумных рекомендаций по методу коллаборативной фильтрации (новый пользователь, пользователь, у которого недостаточно ближайших соседей и т.д.); в таких ситуациях рекомендательные системы тоже часто выдают рекомендации, основанные на своих онлайн-компонентах (см. также недавний пост Василия Лексина о задаче «холодного старта» – мы будем продолжать и ту серию тоже). В качестве хорошего обзора разных методов онлайн-рекомендаций могу порекомендовать эту презентацию; правда, это слайды, а не текст, и там всё очень сжато изложено, так что её лучше использовать как источник ключевых слов и ссылок.

А мы для целей этого поста представим себе такую ситуацию (я её уже упоминал в предыдущей серии). Пусть мы – портал, делаем деньги тем, что размещаем рекламу, и в качестве завлекательного контента нам нужно разместить новостные объявления, по которым пользователи захотят переходить (и видеть ещё больше вкусной рекламы). Внизу – типичная картинка, показывающая (нормализованный) click-through ratio (CTR) нескольких новостей на домашней странице Yahoo; видно, что изменения происходят достаточно быстро, и изменения эти значительны: новости быстро «протухают», и реагировать на это, пересчитывая систему коллаборативной фильтрации раз в сутки, невозможно.

(реальный сэмпл новостей с домашней страницы Yahoo)

Формально говоря, у нас есть набор продуктов/сайтов; мы сейчас хотим оценить CTR каждого из них по отдельности, независимо, поэтому в дальнейшем будем работать с одним из них. Фиксируем период времени t (небольшой) и будем считать показы (общее число экспериментов) и клики (отметки «like» или другие желаемые исходы) за время t. Пусть мы в течение периода t показали сайт n_t раз и получили рейтинг r_t (r_t – целое число, меньшее n_t). Тогда нам в каждый момент времени t дана последовательность 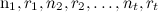, и мы хотим предсказать p_t+1, долю успешных показов (CTR) в момент t+1.

Перечислим первые естественные идеи:

• сортировать по текущему 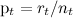; такая сортировка будет действительно быстро реагировать, но, скорее всего, будет реагировать слишком быстро, т.е. будет крайне нестабильной: случайные флуктуации будут оказывать непропорционально сильное воздействие;
• сортировать по общему среднему 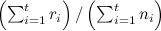; у такого подхода будут обратные проблемы – он крайне медленно будет реагировать на изменения, и уже давно «протухшие» новости останутся в топе;
• сортировать по среднему, подсчитанному по скользящему окну, 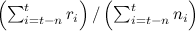; это уже вполне разумная эвристика, но здесь мы не получаем оценки на дисперсию p_t+1, а также не можем подстроиться под разную скорость изменений в разных «ручках».

Для решения этой задачи предлагается использовать так называемую модель dynamic Gamma–Poisson (динамическая гамма–пуассоновская модель, DGP). Вероятностные предположения DGP таковы:

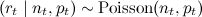• (для фиксированных n_t и p_t получается r_t, распределённое по пуассоновскому распределению);
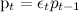• , где 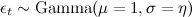(средняя доля успешных показов p_t
  меняется не слишком быстро, а путём умножения на случайную величину ε_t, которая имеет гамма-распределение вокруг единицы);
• Параметрами модели являются параметры распределения ,
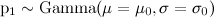  а также параметр η, который показывает, насколько «гладко» может изменяться p_t; соответственно, задача заключается в том, чтобы оценить параметры апостериорного распределения
  

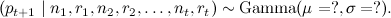
После долгих математических мучений (которые я здесь опущу) получается очень простой итеративный алгоритм для пересчёта параметров этой модели (собственно, конкретная форма распределений была выбрана такой именно для того, чтобы он получался: гамма-распределение является сопряжённым априорным распределением для пуассоновского распределения). Предположим, что на предыдущем шаге t-1 мы получили некоторую оценку μ_t, σ_t для параметров модели:

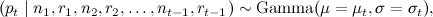
а затем получили новую точку (замеры за новый период времени) n_t, r_t. Обозначим 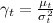(эффективный размер выборки). Тогда мы сначала уточняем оценки μ_t, σ_t:

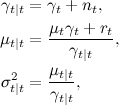
а затем порождаем новое предсказание для :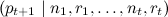

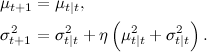
В результате мы для каждого продукта (каждой ручки) будем поддерживать пару чисел 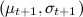, которые будут меняться после каждого периода времени. Список топ-продуктов можно породить, просто упорядочив их п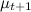о (но 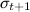забывать всё равно нельзя – дисперсия нужна, чтобы пересчитать потом среднее). Примерное поведение этой модели на части данных с главной страницы Yahoo! показано на рисунке ниже – выглядит неплохо.

(часть сэмпла новостей с предсказаниями модели DGP)

Дальнейшее улучшение этой модели связано с тем, чтобы выбирать хорошие априорные распределения (хорошие μ₀ и σ₀) для новых ручек – это очень важно, потому что новые продукты (например, свежие новости) надо быстро вводить в строй, а поначалу данных о них не так много (тот самый холодный старт). Хорошая оценка априорного распределения получается из отрицательного биномиального распределения – предположим, что у нас есть в базе N исторических записей (N других сайтов), для которых известны показател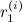и и 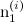(число показов и успешных показов за первый период времени); мы хотим получить оценку μ₀ и σ₀ для нового, неизвестного сайта, которая должна хорошо аппроксимировать ожидаемое r₁ и n₁ для нового сайта. Опять же, математику я опущу, а ответ такой – её нужно считать как

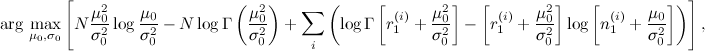
где 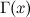– гамма-функция. Максимизировать можно градиентным подъёмом – из точки движемся в сторону градиента, т.е. вектора частных производных.

Уфф. Эта инсталляция получилась заметно более «математической», чем предыдущая. Однако если вы не поняли вероятностного вывода, который произошёл выше, не отчаивайтесь – на выходе, как и прежде, получился простой алгоритм, который очень легко реализовать и который имеет достаточно внятное вероятностное обоснование (разумные предположения в модели). Его можно использовать во всех ситуациях «бандитских» задач, где нужно быстро реагировать на изменения. Например, в том же примере с A/B testing, который я приводил в прошлый раз, вполне может оказаться, что поведение или нужды пользователей со временем меняются, и хочется подстраивать то, что вы тестируете, под текущую ситуацию. А для нас в Surfingbird модель DGP – это важная модель для показа страниц, популярность которых может быстро меняться со временем (та же самая категория «новости», например); так мы быстро понимаем, когда тренд популярности начинает затухать.

В следующий раз мы, наверное, поговорим о какой-нибудь совершенно другой теме; кроме того, следите за обновлениями цикла о холодном старте в рекомендательных системах. До новых текстов!