Чтобы двигаться дальше и поместить эти и многие другие методы в общий контекст, нам нужно выработать некую общую базу, научиться языку, на котором разговаривают современные методы обработки данных, – языку графических вероятностных моделей. Сегодня – первая часть этого рассказа, самая простая, с картинками и пояснениями.
Задачи байесовского вывода
Сначала кратко напомню то, о чём мы уже говорили. Главным инструментом машинного обучения является теорема Байеса:
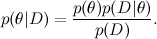
Здесь D — это данные, то, что мы знаем, а θ — это параметры модели, которые мы хотим обучить. Например, в модели SVD данные — это те рейтинги, которые ставили пользователи продуктам, а параметры модели — факторы, которые мы обучаем для пользователей и продуктов.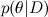 
— это то, что мы хотим найти, распределение вероятностей параметров модели после того, как мы приняли во внимание данные; это называется апостериорной вероятностью (posterior probability). Эту вероятность, как правило, напрямую не найти, и здесь как раз и нужна теорема Байеса. 
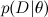– это так называемое правдоподобие (likelihood), вероятность данных при условии зафиксированных параметров модели; это как раз найти обычно легко, собственно, конструкция модели обычно в том и состоит, чтобы задать функцию правдоподобия. А 
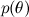— априорная вероятность (prior probability), она является математической формализацией нашей интуиции о предмете, формализацией того, что мы знали раньше, ещё до всяких экспериментов.
Таким образом, мы приходим к одной из основных задач байесовского вывода: найти апостериорное распределение на гипотезах/параметрах:
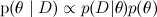
и найти максимальную апостериорную гипотезу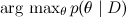 
.
Факторизация сложных распределений и байесовские сети
Но если всё так просто — умножили две функции, максимизировали результат — о чём же здесь целая наука? Проблема заключается в том, что распределения, которые нас интересуют, обычно слишком сложные, чтобы их можно было максимизировать напрямую, аналитически. В них слишком много переменных, между переменными слишком сложные связи. Но, с другой стороны, часто в них есть дополнительная структура, которую можно использовать, структура в виде независимостей (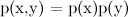
) и условных независимостей (
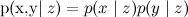) некоторых переменных.
Вспомните наш разговор о наивном Байесе: в модели там получалось неподъёмное число параметров, и мы сделали дополнительное предположение об условной независимости атрибутов (слов) при условии темы:
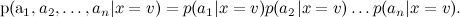
В результате сложное апостериорное распределение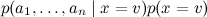 
удалось переписать как
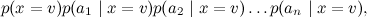
и в этой форме с ним оказалось гораздо проще справиться (обучить параметры каждого маленького распределения по отдельности, а затем выбрать v, дающее максимум произведения). Это один из простейших примеров разложения (факторизации) сложного распределения в произведение простых. Сегодня и в последующих текстах мы сможем обобщить этот метод и довести его до непревзойдённых высот.
Итак, давайте рассмотрим один из самых удобных способов представлять большие и сложные распределения вероятностей – байесовские сети доверия (Bayesian belief networks), которые в последнее время чаще называются просто направленными графическими моделями (directed graphical models). Байесовская сеть – это направленный граф без направленных циклов (это очень важное условие!), в котором вершины соответствуют переменным в распределении, а рёбра соединяют «связанные» переменные. В каждом узле задано условное распределение узла при условии своих родителей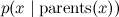 
, и граф байесовской сети означает, что большое совместное распределение раскладывается в произведение этих условных распределений.
Вот, например, граф, соответствующий наивному байесу:
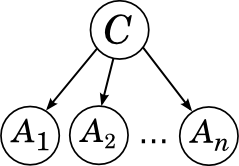
Он соответствует разложению
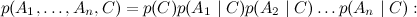
у C нет предков, так что мы берём его безусловное (маргинальное) распределение, а каждый из Ai «растёт» непосредственно из C и больше ни с кем не связан.
Мы уже знаем, что в этом случае все атрибуты Ai условно независимы при условии категории C:
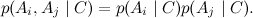
Давайте теперь рассмотрим все простейшие варианты байесовской сети и посмотрим, каким условиям независимости между переменными они соответствуют.
Байесовские сети с двумя и тремя переменными: тривиальные случаи
Начнём с сети из двух переменных, x и y. Здесь всего два варианта: либо между x и y нет ребра, либо есть. Если ребра нет, это просто значит, что x и y независимы, ведь такой граф соответствует разложению .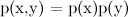
А если ребро есть (пусть оно идёт из x в y, это не важно), мы получаем разложение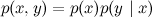 
, которое буквально по определению условной вероятности тупо верно всегда, для любого распределения 
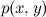. Таким образом, граф из двух вершин с ребром не даёт нам новой информации.
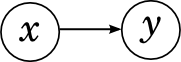
Теперь переходим к сетям из трёх переменных, x, y и z. Самый простой случай – когда рёбер совсем нет.
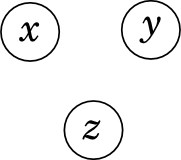
Как и с двумя переменными, это значит, что x, y и z просто независимы: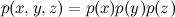 
.
Другой простой случай – когда между переменными проведены все рёбра.
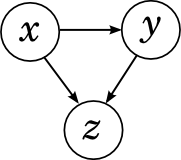
Этот случай тоже аналогичен рассмотренному выше; пусть, например, рёбра идут из x в y и z, а также из y в z. Мы получаем разложение
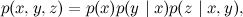
которое, опять же, верно всегда, для любого совместного распределения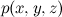 
. В этой формуле можно было бы выбирать переменные в любом порядке, ничего не изменилось бы. Обратите внимание, что направленные циклы в байесовских сетях запрещены, и в результате вариантов, как можно провести все рёбра, всего шесть, а не восемь.
Эти наблюдения, конечно, обобщаются и на случай любого числа переменных: если переменные вообще никак не связаны друг с другом, они независимы, а граф, в котором проведены все рёбра (со стрелочками в любых направлениях, но так, чтобы не получалось направленных циклов), соответствует разложению, которое всегда верно, и не даёт нам никакой информации.
Байесовские сети с тремя переменными: интересные случаи
В этом разделе мы рассмотрим три более интересных случая – это и будут те «кирпичики», из которых можно составить любую байесовскую сеть. К счастью, для этого достаточно рассмотреть графы на трёх переменных – всё остальное будет обобщаться из них. В примерах ниже я несколько погрешу против истины и буду интуитивно интерпретировать ребро, стрелочку между двумя переменными, как «x влияет на y», т.е. по сути как причинно-следственную связь. На самом деле это, конечно, не совсем так – например, часто можно развернуть ребро, не потеряв смысла (вспомните: в графе из двух переменных было всё равно, в какую сторону проводить ребро). Да и вообще это непростой философский вопрос – что такое «причинно-следственные связи» и зачем они нужны. Но для рассуждений на пальцах сойдёт.
Последовательная связь
Начнём с последовательной связи между переменными: x «влияет на» y, а y, в свою очередь, «влияет на» z.
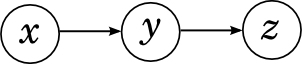
Такой граф изображает разложение
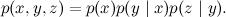
Интуитивно это соответствует последовательной причинно-следственной связи: если вы будете бегать зимой без шапки, вы простудитесь, а если простудитесь, у вас поднимется температура. Очевидно, что x и y, а также y и z друг с другом связаны, между ними даже непосредственно стрелочки проведены. Связаны ли между собой в такой сети x и z, зависимы ли эти переменные? Конечно! Если вы бегаете зимой без шапки, вероятность получить высокую температуру повышается. Однако в такой сети x и z связаны только через y, и если мы уже знаем значение y, x и z становятся независимыми: если вы уже знаете, что простудились, совершенно не важно, чем это было вызвано, температура теперь повысится (или не повысится) именно от простуды.
Формально это соответствует условной независимости x и z при условии y; давайте это проверим:
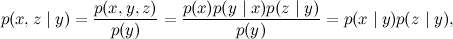
где первое равенство – это определение условной вероятности, второе – наше разложение, а третье – применение теоремы Байеса.
Итак, последовательная связь между тремя переменными говорит нам о том, что крайние переменные условно независимы при условии средней. Всё очень логично и достаточно прямолинейно.
Расходящаяся связь
Следующий возможный вариант – расходящаяся связь: x «влияет» и на y, и на z.
Такой граф изображает разложение
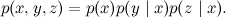
Интуитивно это соответствует двум следствиям из одной и той же причины: если вы простудитесь, у вас может подняться температура, а также может начаться насморк. Как и в предыдущем случае, очевидно, что x и y, а также x и z зависимы, и вопрос заключается в зависимости между y и z. Опять же, очевидно, что эти переменные зависимы: если у вас насморк, это повышает вероятность того, что вы простудились, а значит, вероятность высокой температуры тоже повышается.
Однако в такой сети, подобно предыдущему случаю, y и z связаны только через x, и если мы уже знаем значение общей причины x, y и z становятся независимыми: если вы уже знаете, что простудились, насморк и температура становятся независимы. Disclaimer: мои медицинские примеры крайне условны, на самом деле я понятия не имею, независимы ли в жизни насморк и температура при условии простуды, и даже подозреваю что вряд ли, т.к. многие другие болезни тоже могут вызывать оба этих симптома вместе. Но в нашей условной модели во вселенной нет других болезней, кроме простуды.
Формально это соответствует условной независимости y и z при условии x; проверить это ещё проще, чем для последовательной связи:
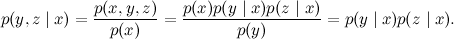
Итак, расходящаяся связь между тремя переменными говорит нам о том, что «следствия» условно независимы при условии своей «общей причины». Если причина известна, то следствия становятся независимы; пока причина неизвестна, следствия через неё связаны. Опять же, пока вроде бы ничего удивительного.
Сходящаяся связь
У нас остался только один возможный вариант связи между тремя переменными: сходящаяся связь, когда x и y вместе «влияют на» z.
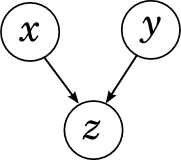
Разложение здесь получается такое:
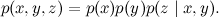
Это ситуация, в которой у одного и того же следствия могут быть две разные причины: например, температура может быть следствием простуды, а может – отравления. Зависимы ли простуда и отравление? Нет! В этой ситуации, пока общее следствие неизвестно, две причины никак не связаны друг с другом, и это очень легко проверить формально:
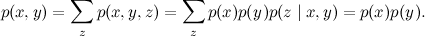
Однако если «общее следствие» z становится известным, ситуация меняется. Теперь общие причины известного следствия начинают влиять друг на друга. Этот феномен по-английски называется «explaining away»: предположим, что вы знаете, что у вас температура. Это сильно повышает вероятность как простуды, так и отравления. Однако если вы теперь узнаете, что отравились, вероятность простуды уменьшится – симптом «уже объяснён» одной из возможных причин, и вторая становится менее вероятной.
Таким образом, при сходящейся связи две «причины» независимы, но только до тех пор, пока значение их «общего следствия» неизвестно; если же общее следствие получает означивание, причины становятся зависимыми.
Но есть, как говорил Василий Иванович, один нюанс: когда на пути встречается сходящаяся связь, недостаточно посмотреть только на её «общее следствие», чтобы определить независимость. На самом деле, если даже у z означивания нету, но оно есть у одного из её потомков (возможно, достаточно далёких), две причины всё равно станут зависимы. Интуитивно это тоже легко понять: например, пусть мы не наблюдаем собственно температуру, а наблюдаем её потомка – показания градусника. На свете, наверное, бывают неисправные градусники, так что это тоже некая вероятностная связь. Однако наблюдение показаний градусника точно так же делает простуду и отравление зависимыми.
Putting it all together
Последовательная, сходящаяся и расходящаяся связи – это те три кирпичика, из которых состоит любой ациклический направленный граф. И наших рассуждений вполне достаточно для того, чтобы обобщить результаты об условной зависимости и независимости на все такие графы. Конечно, здесь не время и не место для того, чтобы формально доказывать общие теоремы, но результат достаточно предсказуем – предположим, что вам нужно в большом графе проверить, независимы ли две вершины (или даже два множества вершин). Для этого вы смотрите на все пути в графе (без учёта стрелочек), соединяющие эти два множества вершин. Каждый из этих путей можно «разорвать» одной из вышеописанных конструкций: например, последовательная связь разорвётся, если в середине у неё есть означивание (значение переменной известно), а сходящаяся связь разорвётся, если, наоборот, означивания нет (причём нет ни в самой вершине из пути, ни в её потомках). Если в результате все пути окажутся разорваны, значит, множества переменных действительно независимы; если нет – нет.
Итак, сегодня мы рассмотрели простое, удобное и важное представление факторизаций сложных распределений – байесовские сети. В следующий раз мы рассмотрим другое (но, конечно, похожее) графическое представление и начнём развивать алгоритмы вывода, т.е. решения задач байесовского вывода в сложных вероятностных моделях.
ссылка на оригинал статьи http://habrahabr.ru/company/surfingbird/blog/176461/
Добавить комментарий