Физический движок для железнодорожного транспорта

Здравствуйте.
В данной статье представлена концепция написания физического движка для железнодорожного транспорта.
Одна из главных задач, которую должен решать данный физический движок – это расчет взаимодействия между вагонами.

Определение коллизий

Железную дорогу можно представить в виде графа, узлами которого являются стрелки. При переводе стрелка соединяет две дуги графа и разрывает связь с третьей. Кривая, состоящая из нескольких дуг графа, по которым может проехать вагон без перевода стрелок, далее будет называться «маршрут».
Взаимодействие между вагонами на одном маршруте происходит в одномерном пространстве. На момент перевода стрелки можно вычислить: какой вагон находится впереди и позади данного вагона. Пока стрелка на маршруте не будет переведена, связи какой вагон спереди, а какой сзади, остаются неизменными.
В трехмерном пространстве остаются проверки боковых столкновений, когда пути проходят очень близко. В таких местах вагоны на разных маршрутах не смогут разъехаться и столкнуться. Для оптимизации расчетов в трехмерном пространстве можно разбить площадь на клеточки и искать столкновения вагонов в рамках данной и соседних клеточках. При этом боковые столкновения между вагонами на одном маршруте проверять не нужно.
Выше перечисленные методы оптимизации расчетов позволяют сделать сложность алгоритма поиска коллизий практически линейно зависимой от количества вагонов.

Концепция взаимодействия вагонов, находящихся на одном «маршруте»

Вагон постоянно обладает импульсом mv.
В момент времени t рассчитываем суммарный вектор сил F=ma. Который изменяет импульс P=mv за этот промежуток времени по формуле:
a=F/m;
v = (v + a*t);
P = m*v;
Где: a – ускорение, m – масса вагона, v – скорость вагона

Взаимодействие с другими вагонами происходит путем передачи импульса между ними.
Алгоритм взаимодействия между вагонами сводится к решению нескольких задач.

Задача:
Необходимо рассчитать координаты и импульсы вагонов через время t. t — интервал времени меньше секунды.
Решение:
Попарно сравниваем все вагоны. Расстояние между вагонами S.
Если расстояние между вагонами сокращается (вагоны идут навстречу друг другу, или один вагон догоняет другой вагон), рассчитываем, сколько времени нужно, чтобы они столкнулись. Находим такое минимальное время tстолкновения.
Ели один вагон сцеплен с другим, и они удаляются друг от друга, то находим, сколько времени требуется, чтобы натянулась автосцепка. Находим минимальное время натяжения автосцепки tнатяжения.
Находим минимальное время взаимодействия между вагонами: tвзаимодействия= min(tстолкновения, tнатяжения).
Если tвзаимодействия>t, то двигаем вагоны на время t и завершаем алгоритм.
Иначе, объединяем столкнувшиеся вагоны в группу, считаем для них общий импульс. Вычитаем время из интервала t=t- tвзаимодействия.
Двигаем все вагоны на расстояние, которое они пройдут в течении времени tвзаимодействия.
Повторяем операцию алгоритма взаимодействия между вагонами, группу считаем как единое целое. При этом если сталкивается группа вагонов с другим телом, и в группе есть натянутая автосцепка, то группы должны быть снова разбиты на отдельные вагоны, так как вагоны внутри группы могут сблизиться.

Упрощения: Так как t – малый промежуток времени, считаем, что импульс вагона изменяется совокупной силой моментально, при этом сила остается неизменной, даже не смотря на то, что вагон меняет координаты и, следовательно, профиль пути. Чтобы увеличить точность можно разбить интервал t на менее длинные промежутки времени и последовательно запустить алгоритм несколько раз.

Задача: Расчет времени до столкновения вагонов.
Есть два вагона или группы вагонов. Между их ближайшими друг к другу точками есть некоторое расстояние S

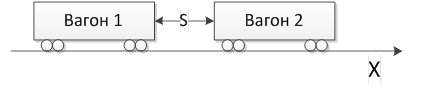
Вагоны имеют некоторую координату X. Значение координаты X у «Вагона 2» больше чем у «Вагона 1». Движение направленное условно вправо будем считать положительным, влево – отрицательным.
Вагон обладает ускорением и начальной скоростью на момент начала вычислительной итерации. Начальная скорость будет обозначаться v1 и v2, ускорение вагонов a1 и a2 соответственно для первого и второго вагона.
Чтобы вагоны столкнулись, они должны сократить расстояние S за некоторое время t. Решение задачи сводится к нахождению времени t.
Упрощение:
Так как временной интервал одной итерации расчетов вычислительной системы может быть достаточно малым, считаем, что профиль пути и прочие внешние факторы, влияющие на вагоны, не могут сильно измениться за этот промежуток времени. Поэтому ускорение на одну итерацию расчета будем считаться постоянным.
Так же в данном алгоритме не учитывается специфика силы трения. Сила трения направлена против движения. И если вагон меняет направления под действием каких-либо сил, то ускорение в этот момент должно значительно измениться, так сила трения поменяет свое направление и окажет свое влияние на ускорение.
Решение:
Каждый вагон до столкновения переместится:
Первый вагон на S1 = v1*t+a1*t*t/2
Второй вагон на S2 = v1*t+a1*t*t/2
Начальное расстояние между вагонами до столкновения есть разница перемещения первого и второго вагона.
S=S1-S2;
S=(v1-v2)*t+(a1-a2)*t*t/2
Получаем квадратное уравнение. Корень этого уравнения будет решением задачи.
Блок схема алгоритма изображена на рисунке. Реализация данного алгоритма на C# изображена в листинге.

/// <summary> /// Расчет времени до столкновения двух групп вагонов /// </summary> /// <param name="s"> /// расстояние между крайними ближайшими друг к другу точками  /// 2-х вагонов в метрах</param> /// <param name="v1">скорость первого вагона м/с</param> /// <param name="v2">скорость второго вагона м/с</param> /// <param name="a1">ускорение первого вагона м/(с*с)</param> /// <param name="a2">ускорение второго вагона м/(с*с)</param> /// <returns> /// Возвращает время в секундах до столкновения двух групп вагонов.  /// Если столкновение не произойдет в ближайшее время при заданной траектории движения /// То может вернуть значение бесконечность (double.PositiveInfinity) /// </returns> public static double ClashTime(double s, double v1, double v2, double a1, double a2){     double A = (a1 - a2) / 2;     double B = v1 - v2;     double T;     if (Math.Abs(A) < 0.000001)    {         if (Math.Abs(B) < 0.000001)        {             T = double.PositiveInfinity;         }         else        {             T = s / B;         }     }     else    {         //Дискриминант квадратного уравнения         double D = B * B + 4 * A * s;         if (D < 0)        {             T = double.PositiveInfinity;         }         else        {             double pD = Math.Sqrt(D) / (2 * A);             double pB = -B / (2 * A);             double t1 = pB + pD;             double t2 = pB - pD;             if (t1 >= 0)            {                 if (t2 >= 0)                     T = Math.Min(t1, t2);                 else T = t1;             }             else            {                 if (t2 >= 0)                     T = t2;                 else T = double.PositiveInfinity;             }         }     }     return T; } 

Задача: Расчет времени до остановки или смены направления движения вагонов
Есть вагон или группа вагонов движущаяся вместе. Вагон имеет начальную скорость V. На вагон действуют различные силы, которые придают ускорения A и сила трения, которая придает ускорение Atr.
Вагон имеет некоторую координату X. Значение координаты X возрастает при движении условно вправо и уменьшается при движении условно влево. То есть направленное условно вправо будем считать положительным, а влево – отрицательным.
Необходимо узнать, сколько времени потребуется, чтобы вагон сменил направление движения или остановился.
Упрощение:
Так как временной интервал одной итерации расчетов вычислительной системы может быть достаточно малым, считаем, что профиль пути и прочие внешние факторы, влияющие на вагоны, не могут сильно измениться за этот промежуток времени. Поэтому ускорение на одну итерацию расчета будем считаться постоянным.
Решение:
Сила трения направлена против направления движения. Поэтому для решения этой задачи нужно найти такой время, при котором скорость снизится до нуля.
KofTr – коэффициент, обозначающий направления силы трения
A – ускорение проекции суммы всех сил, кроме силы трения
Если V>0 то KofTr = -1 иначе KofTr = 1
V0+A*T+ KofTr*Atr*T=0
V0+T*(A+ KofTr*Atr)=0
T=-V0/(A+ KofTr*Atr);

/// <summary> /// Расчет времени до остановки или смены  /// направления движения для группы вагонов /// </summary> public static double StoppingTime(double frictionForceAcceleration,     double otherForcesAcceleration, double speed)  {     double Atr = Math.Abs(frictionForceAcceleration);     double A = otherForcesAcceleration;     double V = speed;     double KofTr;                  if (V == 0)          return 0;                  if (V > 0)          KofTr = -1;      else          KofTr = 1;                  double a = (A+ KofTr*Atr);      //Если a = 0, скорость не изменяется      if (Math.Abs(a) < 0. 0000001)         return double.PositiveInfinity;      //Если V и a направлены в одну сторону      if (a * V > 0)          return double.PositiveInfinity;      double t = -V / a;     return t; } 

Расчет влияния силы тяжести на один вагон

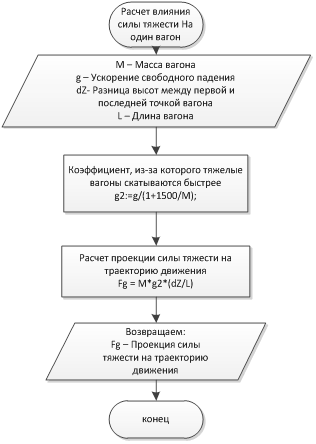
Расчет силы трения, действующий на один вагон

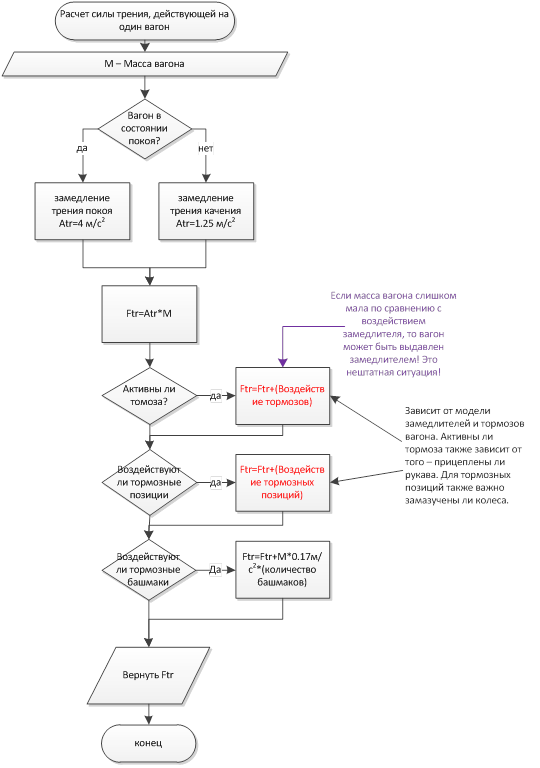
Расчет смещения вагона или связанной группы вагонов

Конечно, это еще только маленькая часть физического движка для железной дороги, об остальном в следующей статье.