Многочлены от нескольких переменных и алгоритм Бухбергера на Haskell

В этой статье я хочу рассказать о том, как реализовывал алгоритмы, связанные с базисами Грёбнера, на языке Haskell. Надеюсь кому-нибудь мои идеи и объяснения окажутся полезными. Я не собираюсь вдаваться в теорию, так что читателю стоит быть знакомым с понятиями полиномиального кольца, идеала кольца и базиса идеала. Советую прочитать вот эту книгу МЦНМО, в ней подробно расписана вся необходимая теория.

Основной предмет статьи — базисы Грёбнера идеалов колец многочленов от нескольких переменных. Это понятие возникает при изучении систем полиномиальных уравнений и даёт очень хороший способ для их решения в большинстве случаев. В конце статьи я на примере покажу, как можно применять эти идеи.

Самый главный результат, который даёт эта теория — хороший способ решать полиномиальные системы уравнений от нескольких переменных. Даже если вы не знакомы с высшей алгеброй или с Haskell, я советую вам прочитать эту статью, так как эти самые методы решения объяснены на уровне, доступном школьнику, а вся теория нужна только для обоснования. Можно спокойно пропустить всё, что связано с высшей алгеброй, и просто научиться решать системы уравнений.

Если вас заинтересовало, прошу под кат.

Я прошу прощения за картинки — это отрендерено latex’ом, а как заставить хабр понимать style="width:...;height=...;" я не знаю. Если подскажете способ лучше, обязательно переделаю.

1 Самые необходимые понятия из алгебры

Множества, на элементах которых можно задать две операции — «сложение» и «умножение», отвечающие определённому набору правил (аксиом), в алгебре называются кольцами. Многочлены от нескольких переменных, коэффициентами которых являются вещественные числа, образуют кольцо, обозначаемое , относительно обычных школьных операций сложения и умножения многочленов. Идеалом кольца называется такое его подмножество, разность двух элементов которого лежит в нём же и произведение любого его элемента и произвольного элемента кольца лежит в этом подмножестве. Самый простой пример идеала — множество кратных пяти чисел как идеал в кольце целых чисел. Самостоятельно убедитесь в том, что это идеал. Если получилось — дальше тоже особых проблем не возникнет.

Далее мы будем рассматривать только идеалы в кольце многочленов. Некоторый конечный набор многочленов называется базисом идеала, если любой многочлен из идеала представим в виде , где — какие-то многочлены. Этот факт записывается так: . Теорема Гильберта о базисе даёт замечательный результат — любой идеал (в кольце многочленов) имеет конечный базис. Это позволяет работать в любой ситуации просто работать с конечными базисами идеалов.

Теперь будем рассматривать системы уравнений следующего вида:

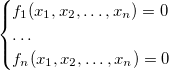
Назовём идеалом этой системы идеал . Из алгебры известно, что любой многочлен, лежащий в идеале 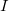, обращается в нуль на любом решении исходной системы. И далее, если 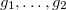— другой базис идеала 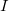, то система

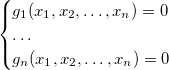
имеет то же множество решений, что и исходная. Из этого всего следует, что если нам удастся найти в идеале системы базис, который проще, чем исходный, то и задача решения самой системы упрощается.

Волшебным образом такой базис существует — он называется базисом Грёбнера идеала. По определению это такой базис, что процедура деления с остатком (о ней позже) для любого многочлена из идеала выдаст нулевой остаток. Если произвести его построение, то один из его многочленов, по крайней мере в большинстве случаев, будет зависеть только от одной переменной, что позволит решить и всю систему последовательной подстановкой.

Последнее, что нам понадобится — -полином и критерий -пар Бухбергера. Выберем какой-нибудь «хороший» способ упорядочивания одночленов (за подробностями — в книжку) и обозначим через старший член (относительно этого упорядочивания) многочлена , а через 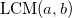— наименьшее общее кратное одночленов и . Тогда -полиномом от и 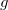называется следующая конструкция:

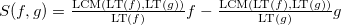
Доказано (критерий -пар), что базис идеала является его базисом Грёбнера тогда и только тогда, когда -многочлен от любой пары его членов даёт остаток 0 при делении на базис (как это делается будет объяснено далее). Это тут же подсказывает алгоритм построения такого базиса:

1. Для каждой пары многочленов базиса составить их -многочлен и разделить его с остатком на базис.
2. Если все остатки равны нулю, получен базис Грёбнера. Иначе, добавить все ненулевые остатки к базису и вернуться на шаг 1.

Это и есть алгоритм Бухбергера — основной предмет этой статьи. На этом с математикой всё, можно переходить. Если вы что-то не поняли, стоит посмотрите википедию или книгу, хотя дальнейшее повествование не требует знаний высшей алгебры.

2 Представление многочленов от нескольких переменных на Haskell

Начнём строить представление многочленов с одночленов. Одночлен характеризуется всего двумя вещами — коэффициентом и набором степеней переменных. Будем считать, что имеются переменные 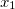, 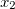и так далее. Тогда одночлен 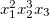имеет коэффициент 1 и степени [2,3,1], а одночлен 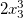— коэффициент 2 и степени [0,0,3]. Обратите внимание на нулевые степени! Они критичны для реализации всех остальных методов. Вообще, потребуем, чтобы списки степеней всех одночленов (в рамках одной задачи) имели одинаковую длину. Это значительно упростит нам работу.

Опишем тип «одночлен» как алгебраический тип данных, состоящий из коэффициента (типа «c») и списка степеней (каждая типа «a»):

data Monom c a = M c [a] deriving (Eq) 

Нам потребуется сравнивать между собой одночлены, так что самое время написать воплощение класса Ord. Я буду использовать обычное лексикографическое упорядочение по степеням, так как оно очень просто и вместе с тем соответствует правилам «хорошего» упорядочения одночленов. Также напишем воплощение класса Show просто для удобства работы с нашей системой.

instance (Eq c, Ord a) => Ord (Monom c a) where     compare (M _ asl) (M _ asr) = compare asl asr  instance (Show a, Show c, Num a, Num c, Eq a, Eq c) => Show (Monom c a) where     show (M c as) = (if c == 1 then "" else show c) ++                      (intercalate "*" $ map showOne $ (filter (\(p,_) -> p /= 0) $ zip as [1..]))         where showOne (p,i) = "x" ++ (show i) ++ (if p == 1 then "" else "^" ++ (show p)) 

Функция show пытается быть «умной»: она не показывает коэффициент, если он равен 1, и она не показывает переменные нулевой степени, а так же не показывает первую степень переменных. Вот так:

 *Main> M 2 [0,1] 2x2 *Main> M 1 [2,2] x1^2*x2^2 

Я буду писать функции, похожие на show, постоянно, так что стоит пояснить, как именно она работает — уверен, кого-нибудь она точно испугала. С помощью zip as [1..] склеиваем каждую степень с номером своей переменной, затем с помощью filter (<br />(p _) -> p /= 0) избавляемся от нулевых степеней, превращаем описание каждой переменной в строку через showOne и, наконец, склеиваем всё вместе, перемежая значками умножения, используя intercalate из Data.List

Теперь мы готовы описать собственно тип многочленов. Для этого подойдёт newtype обёртка над обычным списком:

newtype Polynom c a = P [Monom c a] deriving (Eq)  instance (Show a, Show c, Num a, Num c, Eq a, Eq c) => Show (Polynom c a) where     show (P ms) = intercalate " + " $ map show ms 

На этот раз функция show простая, так как вся грязная работа уже спрятана в типе одночленов. Работает это так:

 *Main> P [M 1 [3,1], M 1 [2,2], M 1 [1,1]] x1^3*x2 + x1^2*x2^2 + x1*x2 

Договоримся на будущее, что одночлены в этом списке всегда будут храниться в порядке убывания (в смысле нашего определения воплощения Ord). Это позволит реализовать некоторые вещи гораздо проще.

3 Операции над многочленами

Самые простые операции это LT, проверки на равенство нулю и умножение на число. Из нашего соглашения об упорядоченности мономов следует, что старший моном всегда стоит на первом месте в списке и может быть получен с помощью head. Одночлен считается нулевым в том случае, если его коэффициент равен нулю, а многочлен — если он не содержит одночленов. Ну а умножение на константу просто изменяет коэффициент:

lt :: Polynom c a -> Monom c a lt (P as) = head as  zero :: (Num c, Eq c) => Monom c a -> Bool zero (M c _) = c == 0  zeroP :: Polynom c a -> Bool zeroP (P as) = null as  scale :: (Num c) => c -> Monom c a -> Monom c a scale c' (M c as) = M (c*c') as 

Два одночлена будут называться подобными, если они отличаются только коэффициентами. Для них определена сумма — нужно просто сложить коэффициенты, а степени оставить без изменения.

similar :: (Eq a) => Monom c a -> Monom c a -> Bool similar (M _ asl) (M _ asr) = asl == asr  addSimilar :: (Num c) => Monom c a -> Monom c a -> Monom c a addSimilar (M cl as) (M cr _) = M (cl+cr) as 

Чтобы перемножить два одночлена, просто сложим степени каждой из переменных. Эту операция очень легко реализовать с помощью замечательной функции zipWith. Я думаю, код говорит сам за себя:

mulMono :: (Num a, Num c) => Monom c a -> Monom c a -> Monom c a mulMono (M cl asl) (M cr asr) = M (cl*cr) (zipWith (+) asl asr) 

Гораздо более интересно сложение многочленов. Будем решать эту задачу рекурсивно. Тривиальные случаи — сумма двух нулевых многочлена (пустых списков) равна нулевому многочлену. Сумма любого многочлена и нулевого равна ему же. Теперь мы можем считать оба многочлена ненулевыми, а значит каждый из них можно разделить на старший член и остальные — «хвост». Возникает два случая:

1. Старшие члены подобны. В этом случае сложим их и добавим результат (если он ненулевой) к сумме хвостов.
2. Старшие члены не подобны. Тогда выберем больший из них. Наше условие упорядоченности гарантирует, что в хвостах обоих многочленов не найдётся подобного ему одночлена. Следовательно, мы можем сложить хвост выбранного многочлена с другим, а затем добавить в его начало этот самый больший одночлен.

Остаётся заметить, что в результате этой рекурсивной процедуры снова получится упорядоченный многочлен, и написать, собственно код.

addPoly :: (Eq a, Eq c, Num c, Ord a) => Polynom c a -> Polynom c a -> Polynom c a addPoly (P l) (P r) = P $ go l r     where            go [] [] = []           go as [] = as           go [] bs = bs           go (a:as) (b:bs) =                if similar a b then                   if (zero $ addSimilar a b) then                       go as bs                   else                       (addSimilar a b):(go as bs)               else                   if a > b then                       a:(go as (b:bs))                   else                       b:(go (a:as) bs) 

Умножение многочленов получается абсолютно естественным путём. Очень просто умножить одночлен на многочлен — просто умножим его на каждый из одночленов с помощью map и mulMono. А затем применим дистрибутивность («распределительный закон», раскрытие скобок) к произведению двух многочленов и получим, что требуется лишь умножить все одночлены первого полинома на второй и сложить полученные результаты. Умножения выполним с помощью всё того же map, а результаты сложим, воспользовавшись foldl’ и addPoly. Код этих двух операций получился на удивление коротким — короче, чем описания типов!

mulPM :: (Ord a, Eq c, Num a, Num c) => Polynom c a -> Monom c a -> Polynom c a mulPM (P as) m = P $ map (mulMono m) as  mulM :: (Eq c, Num c, Num a, Ord a) => Polynom c a -> Polynom c a -> Polynom c a mulM l@(P ml) r@(P mr) = foldl' addPoly (P []) $ map (mulPM r) ml 

Вот и всё, мы реализовали основные действия над многочленами, а значит можно двигаться дальше!

4 Деление с остатком на базис (редукция)

Будем говорить, что одночлен делится на одночлен , если существует такой одночлен , что . Очевидно, что это верно, только если каждая переменная входит в в не меньшей степени, чем в . Следовательно, проверку на делимость можно реализовать с помощью уже знакомой функции zipWith и замечательной функции and. А вместе с проверкой легко получить и собственно процедуру деления:

dividable :: (Ord a) => Monom c a -> Monom c a -> Bool dividable (M _ al) (M _ ar) = and $ zipWith (>=) al ar  divideM :: (Fractional c, Num a) => Monom c a -> Monom c a -> Monom c a divideM (M cl al) (M cr ar) = M (cl/cr) (zipWith (-) al ar) 

Обратите внимание, что теперь тип коэффициента должен позволять деление — класс Fractional. Это удручает, но ничего не поделаешь.
Алгоритм деления многочлена на базис с остатком это, по существу, простое школьное деление столбиком. Среди многочленов базиса выбирается первый такой полином, что на его старший член делится старший член делимого, затем из делимого вычитается этот полином, умноженный на частное их старших членов. Результат вычитания принимается за новое делимое и процесс повторяется. Если старший член не делится ни на один из старших членов базиса, деление завершается и последнее делимое называется остатком.

Нашей основной процедуре деления, назовём её reduceMany, потребуются две вспомогательных — reducable и reduce. Первая из них проверяет, делится ли многочлен на другой, а вторая осуществляет деление.

reducable :: (Ord a) => Polynom c a -> Polynom c a -> Bool reducable l r = dividable (lt l) (lt r)  reduce :: (Eq c, Fractional c, Num a, Ord a) =>           Polynom c a -> Polynom c a -> Polynom c a reduce l r = addPoly l r'     where r' = mulPM r (scale (-1) q)           q = divideM (lt l) (lt r) 

Так как у нас нет функции для вычитания, просто умножим второй многочлен на -1 и сложим их — всё просто! А вот и весь алгоритм деления:

reduceMany :: (Eq c, Fractional c, Num a, Ord a) =>               Polynom c a -> [Polynom c a] -> Polynom c a reduceMany h fs = if reduced then reduceMany h' fs else h'     where (h', reduced) = reduceStep h fs False           reduceStep h (f:fs) r                | zeroP h = (h, r)               | otherwise = if reducable h f then                                 (reduce h f, True)                             else                                 reduceStep h fs r           reduceStep h [] r = (h, r) 

Функция reduceMany пытается поделить многочлен на базис. Если деление произошло, процесс продолжается, иначе — завершается. Внутренняя функция reduceStep всего лишь ищет тот самый первый многочлен, на который можно поделить, и делит, возвращая остаток и флаг, показывающий, было ли сделано деление.

5 Алгоритм Бухбергера

Вот мы и подошли к основной части этой статьи — реализации алгоритма Бухбергера. Единственное, чего у нас ещё нет, это функции для получения -полинома. Её реализация очень проста, как и вспомогательной функции для поиска наименьшего общего кратного одночленов:

lcmM :: (Num c, Ord a) => Monom c a -> Monom c a -> Monom c a lcmM (M cl al) (M cr ar) = M (cl*cr) (zipWith max al ar)  makeSPoly :: (Eq c, Fractional c, Num a, Ord a) =>              Polynom c a -> Polynom c a -> Polynom c a makeSPoly l r = addPoly l' r'     where l' = mulPM l ra           r' = mulPM r la           lcm = lcmM (lt l) (lt r)           ra = divideM lcm (lt l)           la = scale (-1) $ divideM lcm (lt r) 

Здесь оба полинома просто умножаются на соответствующие одночлены, причём второй дополнительно ещё и на минус единицу, как и в случае деления с остатком.
Я уверен, что существует множество способов реализовать этот алгоритм. Я также не претендую на то, что моя реализация достаточно оптимальна или проста. Но она мне нравится и она работает, и это всё, что требуется.

Подход, который я использовал, можно назвать динамическим. Разделим наш базис на две части — ту, в которой мы уже проверили (и добавили) -полиномы от всех пар — «checked» — и ту, в которой только предстоит сделать это — «add». Один шаг алгоритма будет выглядеть так:

1. Возьмём первый многочлен из второй части
2. Последовательно построим -полиномы между ним и всеми многочленами первой части и добавим все ненулевые остатки в конец второй части
3. Переместим этот многочлен в первую часть

Как только вторая часть окажется пустой, первая будет содержать базис Грёбнера. Преимущество такого решения в том, что не будут считаться -полиномы от тех пар, от которых они уже посчитаны и проверены. Ключевая функция в этом процессе — checkOne. Она принимает многочлен (из второй части), а так же обе части, а возвращает список многочленов, которые следует добавить к базису. Используем простую рекурсию по первой части, естественно не добавляя нулевые остатки:

checkOne :: (Eq c, Fractional c, Num a, Ord a) =>             Polynom c a -> [Polynom c a] -> [Polynom c a] -> [Polynom c a] checkOne f checked@(c:cs) add = if zeroP s then                                    checkOne f cs add                                else                                    s:(checkOne f cs (add ++ [s]))     where s = reduceMany (makeSPoly f c) (checked++add) checkOne _ [] _ = [] 

Наверняка это можно заменить на хитрый foldl, но я оставлю это в качестве упражнения. Осталось лишь построить сам базис Грёбнера по данному. Реализация шага алгоритма дословно повторяет его описание, смотрите сами:

build checked add@(a:as) = build (checked ++ [a]) (as ++ (checkOne a checked add)) build checked [] = checked 

Многочлен a переходит в первую часть, а во вторую попадают все его ненулевые остатки. Обратите внимание, что и правда достаточно проверять -полиномы каждого многочлена второй части только с первой, в силу перемещений полиномов между частями. Остаётся заметить, что для получения базиса Грёбнера из данного достаточно поместить один его многочлен в первую часть, остальные — во вторую и применить процедуру build, что и сделано в функции makeGroebner.

makeGroebner :: (Eq c, Fractional c, Num a, Ord a) =>                 [Polynom c a] -> [Polynom c a] makeGroebner (b:bs) = build [b] bs     where build checked add@(a:as) = build (checked ++ [a]) (as ++ (checkOne a checked add))           build checked [] = checked 

6 Примеры использования

Все эти теоретические построения кажутся совершенно бесполезными без демонстрации практического применения этих методов. В качестве примера рассмотрим задачу нахождения точки пересечения трёх окружностей — простейший случай позиционирования на карте. Запишем уравнения окружностей как систему уравнений:

.

После раскрытия скобок получаем следующее:

Построим базис Грёбнера (я использовал тип Rational для пущей точности):

 *Main> let f1 = P [M 1 [2,0], M (-2) [1,0], M 1 [0,2], M (-26) [0,1], M 70 [0,0]] :: Polynom Rational Int *Main> let f2 = P [M 1 [2,0], M (-22) [1,0], M 1 [0,2], M (-16) [0,1], M 160 [0,0]] :: Polynom Rational Int *Main> let f3 = P [M 1 [2,0], M (-20) [1,0], M 1 [0,2], M (-2) [0,1], M 76 [0,0]] :: Polynom Rational Int *Main> putStr $ unlines $ map show $ makeGroebner [f1,f2,f3] x1^2 + (-2) % 1x1 + x2^2 + (-26) % 1x2 + 70 % 1 x1^2 + (-22) % 1x1 + x2^2 + (-16) % 1x2 + 160 % 1 x1^2 + (-20) % 1x1 + x2^2 + (-2) % 1x2 + 76 % 1 (-20) % 1x1 + 10 % 1x2 + 90 % 1 15 % 1x2 + (-75) % 1 

Чудесным образом мы получили два линейных уравнения, которые быстро дают ответ — точка (7,5). Можно проверить, что она лежит на всех трёх окружностях. Итак, мы свели решение системы трёх сложных квадратных уравнений к двум простым линейным. Базисы Грёбнера — действительно полезный инструмент для подобных задач.

7 Вопросы для размышления и заключение

На самом деле, этот результат можно ещё улучшить. -полиномы требуется считать только для тех пар многочленов, старшие члены которых не взаимно просты — то есть их наименьшее общее кратное не является просто их произведением. В некоторых источниках про этот случай говорят «многочлены имеют зацепление». Добавьте такую оптимизацию в нашу функцию makeGroebner.

Если в итоговый базис попал полином, старший член которого делится на старший член какого-то другого полинома из базиса, то его можно исключить. Базис, полученный после исключения всех таких многочленов, называется минимальным базисом Грёбнера. Также можно рассмотреть полином, произвольный член которого делится на старший член какого-то другого полинома. В этом случае заменим этот полином остатком от деления на другой. Базис, в котором проведены все возможные операции такого типа, называется редуцированным. В качестве упражнения реализуйте минимизацию и редуцирование базиса.

В заключение хочу сказать спасибо всем, кто дочитал эту статью до конца. Я знаю, что моё повествование было несколько сумбурным, а код неидеальным (и, может, непонятным), но я всё-таки надеюсь, что заинтересовал кого-нибудь базисами Грёбнера. Мне будет очень приятно, если кто-нибудь сможет найти применение моим наработкам в хоть сколько-нибудь реальных задачах.

Весь код из статьи доступен в виде gist.