В начале 2012 года мы впервые столкнулись с проблемой — движок, который до этого использовался в десктопной версии, оказался слишком требовательным к ресурсам и его невозможно использовать на мобильных устройствах. Нужно было что-то делать.
Почему не взять готовые решения?
Существует мнение, что движок роутинга — это неподъемная задача с кучей тонкостей реализации. Будто за то, что не лезет в boost::graph и браться не стоит (про что не снято кино, того и знать не положено, да) и проще найти уже готовое решение. Возможно, но не в нашем случае.
Надеюсь, что из статьи станет понятно — здравый смысл, немного авантюризма и готовое на всё руководство позволяют решить любую задачу.
Справедливости ради, следует отметить, что я уже имел опыт работы с поиском в графах (~50 млн вершин), поэтому некоторые представления о том, как надо решать подобные задачи, уже были.
Итак, вводная:
- В серверной версии должен работать тот же код, но с другими настройками;
- Построение пути должно работать на мобилках за разумное время;
- В активе готовый (и выверенный) дорожный граф; это оказалось гораздо проще/удобней/дешевле, чем поиск и заточка готовых решений.
Обозначим основные (и, банальные, в общем-то) принципы:
- Структуры хранения должны быть простыми.
- Полезно стимулировать локальность ссылок, т.е. если данные относятся к физически близким (например) вершинам графа, то и на диске им по возможности следует располагаться неподалеку.
- К элементам графа на диске ни в коем случае не следует обращаться по одному, чтение осуществляется только пачками.
- От низкоуровневого кэширования мало толку, заботиться следует только о “дорогостоящих” объектах. Например, вместо того, чтобы кэшировать непосредственно дисковые обращения, лучше позаботиться о минимизации их числа алгоритмическим путем.
- Логику поиска в графе стоит упрощать, где это возможно, ибо “if ломает конвейер”(С)
- Сжимать данные на диске — хорошо.
- Пренебрегать точностью в пользу производительности — не предосудительно.
Основные идеи
- Посадим координаты вершин на решетку. Т.е. переведем координаты с плавающей точкой в целые числа. Решетку можно делать достаточно грубой, увеличивая ее шаг до тех пор, пока не начнут слипаться вершины или, что еще хуже, образовываться ребра нулевой длины. При поиске нам координаты будут нужны для оценки оставшегося до финала расстояния (и для отладки) и при решетке с большим шагом, недалеко от финиша алгоритм начнет вести себя странно.
Отметим, что, чем грубей решетка, тем меньше будет объем данных на диске, поэтому, если очень хочется, ее можно подобрать итеративно. У нас шаг решетки — метр.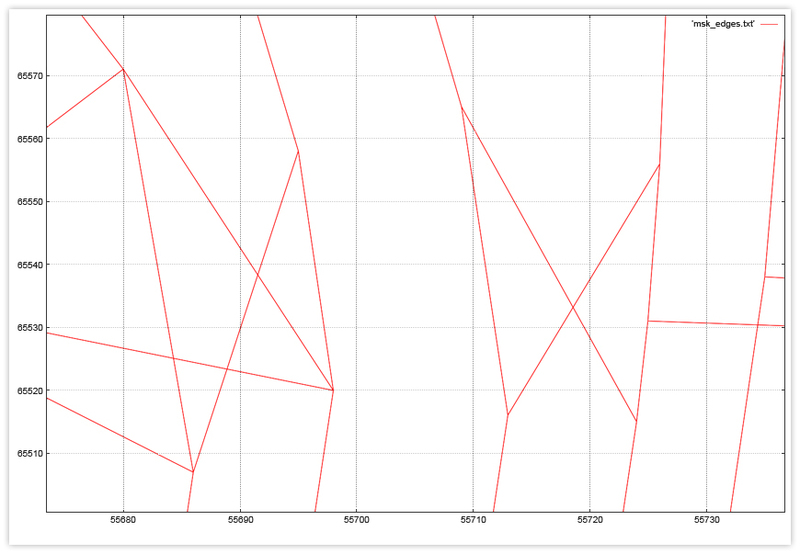
Вот так выглядит фрагмент графа, посаженный на решетку.
- Поделим мысленно экстент нашего графа на некоторое количество прямоугольных тайлов, образующих решетку. Решетка эта не обязана быть подрешеткой оной у вершин.
- Тайл — логическая единица, подлежащая одномоментной загрузке с диска и кэшированию. Содержит в себе все вершины и исходящие дуги (т.е. дуги, начальные вершины которых лежат в этом тайле). Плюс сопутствующая информация, если таковая есть.

Пример ребер, попавших в один тайл на примере фрагмента дорожного графа Москвы.
- Размер тайла следует выбирать исходя из размера графа. Раз мы будем загружать что-то с диска, разумным будет, чтобы общее количество прочитанной информации было соизмеримо с размером дискового буфера. Было бы странно использовать тяжелую артиллерию в виде дисковых обращений для доступа к нескольким вершинам, умещающимся в сотню байт. Конечно, граф устроен неравномерно, но можно апеллировать к средним значениям, Например, граф занимает на диске 20мб, т.е. 2500 8К страниц, следовательно пилим экстент графа на 50×50 частей (sqrt(2500)). Здесь неявно предполагается, что вся информация о тайле лежит в одном месте. Если это не так, надо сделать соответствующую поправку.
- Есть смысл кэшировать именно тайлы.
- Загруженный в память граф (или его часть) — большое количество мелких объектов. Нельзя безнаказанно выделять и освобождать большие количества мелких объектов. Поэтому мы будем использовать сеансовые страничные аллокаторы, там, где это возможно. Помимо скорости и существенно меньшей фрагментации памяти, это даст еще и экономию на прологе и эпилоге блока данных (имеется ввиду алгоритм с двойными метками).
Страничный аллокатор раздает память из принадлежащих ему страниц фиксированного размера (по возможности), которые выпрашивает у системы по мере необходимости. Освобождается память только вся сразу в его деструкторе. - Тайл обязательно будет обладать таким аллокатором, все, что будет выделяться при его загрузке будет браться из него и умрет вместе со своим тайлом, когда тот будет вытеснен из кэша.
- Еще один кандидат на использование страничного аллокатора — собственно поиск, информацию о пройденной части графа удобно хранить именно таким образом
- Собственно алгоритм поиска. Будем использовать обыкновенный А*, одной “волной”, с оценкой стоимости вершины в виде суммы пройденного пути (или времени) и оценки оставшегося.
- А* — т.к. он позволяет уменьшить количество пройденных вершин по сравнению с оригинальным алгоритмом Дейкстры.
- Одной волной — по двум причинам. Во-первых, запуск двух волн навстречу хоть и сократит пройденную часть графа, но усложнит критерий остановки т.к. мы должны постоянно проверять не столкнулись ли две волны. А это влечет за собой либо содержание каждой волной динамического набора пройденных вершин, либо модификацию непосредственно загруженных тайлов.
- Вторая причина — наличие встречной волны не позволит динамически влиять на стоимость ребер, например, вследствие изменения дорожной обстановки к тому моменту, как мы мысленно доберемся до этого ребра.
- Оценка стоимости оставшегося пути может быть любая, при условии, что не нарушено неравенство треугольника. Например, можно использовать честное евклидово расстояние или расстояние Чебышева.
Исходные данные
- Вершины графа — структуры, имеющие координаты и идентификатор
- Ребра содержат идентификатор, длину, тип и идентификаторы начальной и конечной вершин. Все ребра однонаправленные.
- Ограничения — пары ребер, переход между которыми невозможен. Ограничение привязано к конкретной вершине, общей для обоих ребер. Мы описываем такой довольно усеченный вариант ограничений, при необходимости читатель без труда придумает обобщение.
Предобработка
- Находим включающий экстент графа.
- Определяемся с решеткой координат.
- Определяемся с решеткой тайлов. Каждому тайлу присваивается его идентификатор. Идентификатором служит нарастающий в результате работы какой-то заметающей кривой номер. Такой кривой может быть строчная развертка (igloo), кривая Гильберта или bit interleaving curve (zorder). По большому счету, важно лишь уметь по координатам точки уметь определять в какой тайл она попадает. А выбор заметающей кривой влияет лишь на способность данных к сжатию.
- Приписываем каждую вершину к конкретному тайлу. При этом, присваиваем каждой вершине ее порядковый номер в ее тайле, это тоже полезно для сжатия.
- Для каждого ребра определяем, из какого тайла оно выходит и в какой попадает, а также внутренние номера исходящей и входящей точек.
Хранение на диске
Собственно данные хранятся в В-деревьях, точнее в одной из их разновидностей.
От хранилища данных нам нужна способность хранить сортированный массив N-ок и быстро вычитывать их интервалы.
По большому счету, выбор хранилища не принципиален, мы выбрали В-деревья, т.к они:
- Просты в понимании и отладке
- Позволяют сжимать данные, не привязываясь к специфике
- Самое главное, под рукой была оттестированная их реализация.
Итак, есть несколько деревьев:
1. Дерево вершин. N-ка этого дерева состоит из 4 элементов:
- Идентификатор тайла вершины
- Порядковый номер вершины в этом тайле
- X — координата точки
- Y — координата точки.
2. Дерево ребер, Его ключ состоит из 7 элементов:
- Идентификатор тайла исходящей вершины
- Номер исходящей вершины в ее тайле
- Идентификатор тайла входящей вершины
- Номер входящей вершины в ее тайле
- Стоимость ребра, например, длина
- Тип ребра, например, класс дороги
- Внешний идентификатор ребра.
3. Дерево идентификаторов. Служит для связи с внешним миром. Ключ содержит 5 элементов:
- Внешний идентификатор ребра
- Номер тайла исходящей вершины
- Номер исходящей вершины в ее тайле
- Номер тайла входящей вершины
- Номер входящей вершины в ее тайле.
4. Дерево ограничений с ключом длины 4:
- Номер тайла вершины ограничения.
- Номер этой вершины в тайле
- Внешний идентификатор ребра, из которого запрещено движение
- Внешний идентификатор ребра, куда запрещено движение.
Вдумчивый читатель скажет: «Ба! Чтобы прочитать всю информацию об одном тайле надо делать 3 строка по деревьям. Не лучше ли запаковать всё в BLOB и поднимать его одним махом?» Для read-only данных лучше, конечно, и в скорости и по качеству сжатия. Но это дополнительная работа, дополнительное тестирование. Кроме того, профилирование показало, что, собственно, вычитывание данных не является узким местом при поиске проезда.
Если же речь идет о данных, которые могут динамически меняться, здесь В-деревья вне конкуренции. Не обязательно даже иметь собственную реализацию деревьев, можно использовать SQL-хранилище, а вышеописанные сущности задавать как таблицы, состоящие из одного только primary key. Так, один из предшественников описываемого движка был построен на базе СУБД OpenLink Virtuoso, где сами таблицы устроены, как деревья и, в нашем случае, отсутствует дублирование данных как таковое (имеется ввиду дублирование данных из таблицы в индексе).
Представление графа в памяти
В этом разделе опишем, как выглядит распакованный граф в памяти.
1. Весь граф в памяти может и не существовать. Как уже говорилось, он подгружается потайлово по мере того, как кому-то потребовались части этого графа.
2. Следовательно, есть кэш тайлов и держатель этого кэша. Стратегия кэширования может быть любой. У нас это LRU (Least Recently Used).
3. Загруженный в память тайл — содержит всю информацию о данных, попавших в его область пространства. Как уже говорилось, вся память для этого выделяется из принадлежащего тайлу аллокатора и освобождается при его кончине. А именно:
- struct vertex_t {int x_; int y_; const link_t*links_; }; Описывает вершину, выделяются пачкой т.к. внутри каждого тайла своя нумерация. Указатель links_ смотрит на терминированный нулем список ребер, выходящих из данной вершины.
- struct link_t {
int64_tfid_; // внешний идентификатор ребра
int len_; // длина
int class_; // тип
int vert_id_; // номер входящей вершины, >0, если в том же тайле
union {
const vertex_t *vertex_;
// следующее ребро
};
struct restriction_t {uint64_t from_; uint64_t to_;}; Описатель ограничения движения. Их относительно немного и дешевле содержать отдельный набор ограничений, чем добавлять (скорее всего) пустой указатель на список ограничений в каждый описатель вершины. Впрочем, это дело вкуса.
4. Таким образом, тайл в памяти — это готовый к использованию кусок графа, который умеет:
- Выдавать вершину по номеру
- Определять по вершине исходящие ребра
- Тестировать пару ребер на предмет ограничения по ней
- Ребра — это либо указатели при переходе внутри тайла, либо пара номер- тайла / номер-вершины в противном случае. По этой паре при продвижении по графу можно прозрачно спросить нужный тайл у держателя кэша, подгрузить его при необходимости и переключиться на него.
Собственно поиск
1. Перед началом поиска нужно привязаться к графу. Т.е. снаружи мы получаем два набора точек — исходных и конечных. Описание каждой точки состоит из ее внешнего идентификатора ребра графа и стоимости. Стоимости достижения начала этого ребра для исходной точки и стоимости пути от конца ребра до финала для конечной точки. Итак:
2. С помощью дерева идентификаторов мы превращаем идентификаторы ребер в точки входа в граф (const vertex_t *). Для этого придется обратиться к держателю кэша тайлов и подгрузить нужные из них.
Нам нужен объект — держатель информации о финале, включая идентификаторы тайлов и номера вершин. Еще одна полезная информация, которой обладает этот объект, — геометрическое положение финиша. Ее можно задавать явно, а можно вычислять, например, как центроид финальных точек. Эта точка нам будет нужна для вычисления оценочной части стоимости достигнутой вершины для алгоритма А*
3. Теперь нам нужен держатель «волны». Он состоит из:
a. Аллокатора, ну куда ж без него.
b. Набора подгруженных тайлов. Для графов разумной величины достаточно битовой маски. Т.е., когда мы первый раз попали в какой-либо тайл, помечаем соответствующий бит в этой маске и наращиваем счетчик его ссылок. После завершения поиска, ориентируясь на эту маску, мы откатим счетчики ссылок обратно. При этом, те тайлы, чьи счетчики обнулились, получают в дальнейшем шанс вылететь из кэша.
c. Приоритетная очередь. Мы используем бинарную сортирующую кучу. В очередь попадают кандидаты на просмотр. Например, стартовые точки попадают прямиком сюда. Ключом при этом являются пройденное расстояние либо потраченное время. А значением — указатель на описатель пройденной точки
d. Набора пройденных точек. Каждая такая точка описывается структурой:
struct vertex_ptr_t {
int64_t fid_; // внешний идентификатор ребра, из которого мы сюда попали
// для стартовых точек это 0
const vertex_t *ptr_; // указатель на точку в графе
const vertex_ptr_t *prev_; // указатель на предыдущую пройденную точку
size_t cost_len_; // пройденное на данный момент расстояние
size_t cost_time_; // потраченное на данный момент время
};
Конечно, эти структуры выделяются аллокатором.
4. Итак, для каждой стартовой точки мы создаем ее описатель и помещаем его в кучу. Вот мы и готовы начинать поиск.
5. Пока в куче что-то есть (и пока это что-то потенциально лучше уже найденных кандидатов), выбираем из нее самый дешевый элемент и:
a. бежим по списку его исходящих ребер и для каждого из них:
I. проверяем возможность перехода на это ребро с предыдущего.
II. находим вершину графа, на которую указывает это ребро. Возможно, при этом будет подгружен новый тайл, и эта точка будет в нем.
III.Вычисляем стоимость достижения этой новой точки. Для этого:
- берем накопленные путь и время
- суммируем путь с длиной текущего ребра
- время наращиваем на величину, которая нужна на преодоление текущего в соответствии с его длиной, типом и чем угодно еще
- вычисляем и добавляем оценку оставшегося пути — abs(dx) + abs(dy), где dx и dy — разница по долготе и широте соответственно
- вычисляем и добавляем оценку оставшегося до финиша времени исходя из оценки оставшегося пути, времени суток, средней скорости на
- пройденном этапе и чего угодно еще
IV. создаем и наполняем описатель пройденной вершины
V. проверяем, не является ли финальной эта точка
VI. если это финиш, то раскручиваем список предыдущих
( vertex_ptr_t::prev_ ), начиная с данной точки, пока на упремся в 0,
т.е. в старт. Вот и готовый кандидат на выдачу.
VII. заносим созданный описатель в кучу
Результаты
Попробуем оценить результаты содеянного на примере дорожного графа столицы нашей необъятной Родины.
- Граф содержит 307338 вершин
- И 806220 ребер.
- Размеры экстента — 92 x 112 км
- Количество тайлов — 46 x 56 = 2576 штук
- Общий объем данных на диске, занимаемый дорожным графом 13 980 кб
- Средняя длина вычисляемого пути — 32.8 км
- Например,
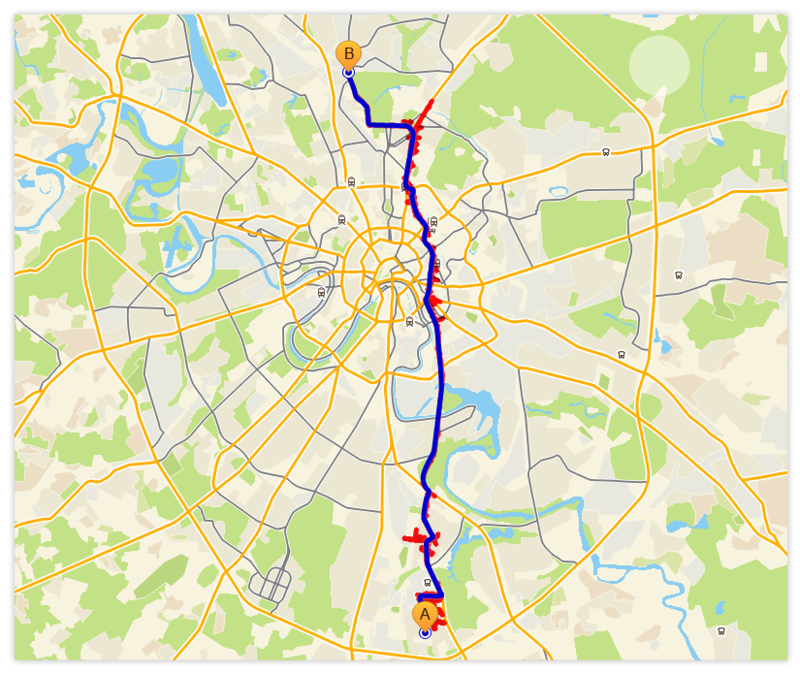
Синим обозначен оптимальный маршрут, красным — “волна”.
- При этом в среднем затрагивается 1644 вершин и 2406 ребер, лежащих на 22 тайлах
- При этом требуется 2096 кб для тайлов и 116 кб для волны
- потраченное время на Sony Xperia S 400+500 (на инициализацию индекса) мс (IPhone 4 800+1000 (…) мс)
- Пример, путь через весь граф
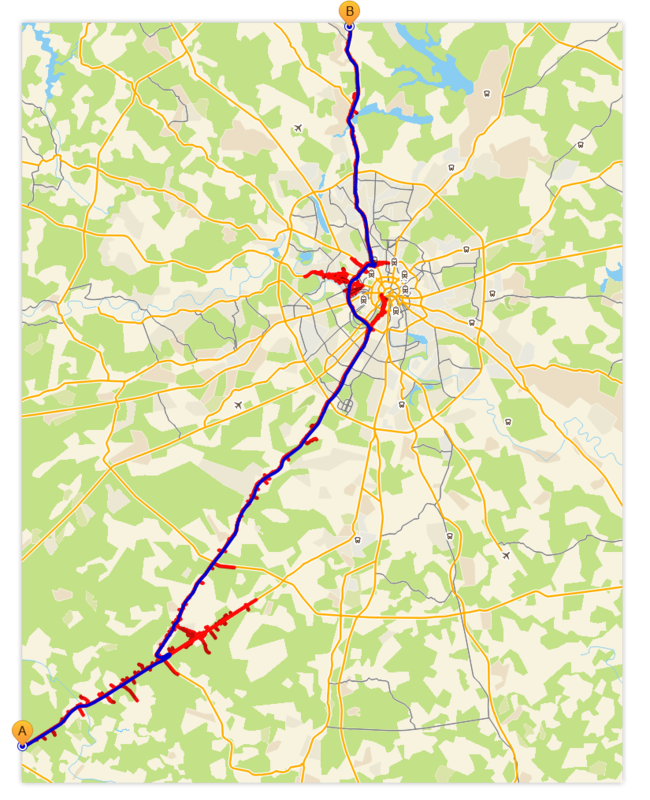
Как и раньше, синим обозначен оптимальный маршрут, красным — “волна”.
Забавно наблюдать, как поиск выявил (фактическое, неявное) иерархическое устройство графа и стал его использовать
- Его вычисленная длина — 135.3 км
- При этом затрагивается 2251 вершин и 3044 ребер, лежащих на 120 тайлов
- При этом требуется 3 946 кб для тайлов и 133 кб для волны
- потраченное время 400 мс Sony Xperia S (500 IPhone 4) плюс та же разовая загрузка индекса, конечно
- А вот демонстрация того, насколько важна используемая эвристика — три картинки проезда по Новосибирску с разными настройками:

Итого
Как мы видим, столь простая структура данных и описанный алгоритм, позволяют работать с одноуровневым графом большого города на рядовом смартфоне. А если нам позволяет оперативная память, например, в серверном случае, увеличивая размер кэша тайлов мы просто загоняем весь граф в память и работаем с готовым его представлением. Что благотворно сказывается на производительности.
Мы намеренно не касались некоторых моментов, например, учета дорожной обстановки, предсказания оной, иерархических графов, ибо это совсем другая история.
That’s All Folks!
ссылка на оригинал статьи http://habrahabr.ru/company/2gis/blog/179749/
Добавить комментарий