
Понятие энтропии используется практически во всех областях науки и техники,
от проектирования котельных до моделей человеческого сознания.
Основные определения как для термодинамики, так и для динамических систем и способы вычисления понять не сложно. Но чем дальше в лес — тем больше дров. Например, недавно выяснил (благодаря Р. Пенроуз, «Путь к реальности», стр 592-593), что для жизни на Земле важна не просто солнечная энергия, а её низкая энтропия.
Если ограничится простыми динамическими системами или одномерными массивами данных (которые могут быть получены как «след» движения системы), то и тогда можно насчитать минимум три определения энтропии как меры хаотичности.
Самое глубокое и полное из них (Колмогорова-Синая) можно наглядно изучить,
используя программы — архиваторы файлов.
Введение
Упоминая информационную энтропию, нередко просто приводят «волшебную» формулу Шеннона:

где N — количество возможных реализаций, b — единицы измерения (2 — биты, 3 — триты,..), pi — вероятности реализаций.
Разумеется, всё не так просто (зато интересно!). Для первого (а также второго, и даже третьего) знакомства, рекомендую ничуть не устаревшую книгу А.Яглом, И.Яглом «Вероятность и информация», 1973.
В качестве ответа на «детский» вопрос: "Что же означает число, полученное по формуле?"
подойдёт такая наглядная иллюстрация.
Пусть имеется N = 16 клеток, одна из которых помечена крестиком:
[ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [x] [ ] [ ] [ ] [ ]
Выбор случаен; вероятность того, что помечена i-тая клетка равна pi = 1/16
Энтропия Шеннона равна
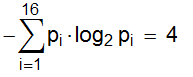
А теперь представим себе игру; один игрок рисует клетки, ставит крестик и сообщает второму только
количество клеток. Второй должен узнать, какая из них помечена и задаёт вопросы;
но первый будет отвечать только «Да» или «Нет».
Сколько (минимум!) вопросов надо задать, чтобы узнать, где крестик?
Ответ — "4". Во всех подобных играх минимальное число вопросов будет равно информационной энтропии.
При этом не имеет значения, какие вопросы задавать. Пример правильной стратегии —
разделить клетки пополам (если N — нечётное, то с избытком/недостатком в 1 клетку) и спросить:
«Крестик в первой половине?» Узнав, что в такой-то, делим и её пополам и т.д.
Другой вроде «наивный», но глубокий вопрос: почему в формуле Шеннона присутствует логарифм?
А что такое, собственно, логарифмическая функция? Обратная показательной… А что такое показательная?
На самом деле, строгие определения даются в курсе матанализа, но они совсем не сложные.
Часто бывает, что увеличивая «вход» в разы, мы получаем «выход» лишь на сколько-то единиц больше.
Огюстен Коши доказал, что уравнение
f(x · y) = f(x) + f(y) x,y>0
имеет только одно непрерывное решение; это и есть логарифмическая функция.
Представим теперь, что мы проводим два независимых испытания; количество исходов у них n и m, все они равновероятны (например, бросаем одновременно игральную кость и монету; n = 6, m=2)
Очевидно, число исходов двойного опыта равно произведению n · m.
Неопределённости же опытов складываются; и энтропия, как мера этой неопределённости, должна
удовлетворять условию h(m · n) = h(m) + h(n), т.е. быть логарифмической.
Энтропия Колмогорова-Синая
Строгое определение этого фундаментального понятия довольно сложно для понимания.
Подойдём к нему постепенно;
нашим «фазовым пространством» будут одномерные массивы натуральных чисел.
Например, десятичные цифры числа «Пи»: {3, 1, 4, 1, 5, 9, 2, 6,…}
На самом деле, к такому виду можно привести любые данные (с потерями, конечно).
Достаточно весь диапазон значений разбить на N интервалов и при попадании в k-тый интервал записывать число k (как при семплинге звука).
Насколько случайна, стохастична та или иная последовательность?
Информационная энтропия, конечно, является хорошим кандитатом на «измеритель хаоса».
Нетрудно доказать, что она максимальна, когда все вероятности появления различных чисел равны.
Но дальше начинаются трудности, о которых я упоминал в предыдущем посте.
Например, массив …010101010101010101… имеет максимальную энтропию, будучи наименее случайной последовательностью из 0 и 1.
Если данные изначально не цифровые (звук, картинки), то конвертировать их в числа от 0 до N можно разными способами. А вероятности в числовом массиве можно мерить не только для отдельных элементов, но и для пар, троек, нечётных по порядку и т.д.
Что ж, раз вариантов много, используем их все!
Будем отображать «подопытный» массив всевозможными способами — в различных системах счисления, разбивая на пары и тройки и т.д. Очевидно, его размер L и энтропия Шеннона H будут зависеть от способа отображения.
Например, считая его цельным, неделимым объектом, получим L = 1, H = 0.
Учитывая, что H растёт с увеличением L, введём величину

Это и есть (несколько упрощённое) определение энтропии Колмогорова-Синая (вот строгое). В теоретическом смысле оно совершенно.
А вот технически найти верхнюю грань по всем разбиениям очень сложно. К тому же, для наглядности надо будет расположить все результаты упорядоченно, а это отдельная серьёзная задача.
К счастью, существует подход, почти не ослабляющий строгости теории, но гораздо более наглядный и
практичный.
Архивация и энтропия
О методах и алгоритмах сжатия информации на Хабре рассказывалось не раз,
habrahabr.ru/post/142242/
habrahabr.ru/post/132683/
не говоря уже об оригинальных источниках.
В своё время возможность сжатия до 50% с полным восстановлением произвела на меня шокирующее впечатление.
Не менее удивлён был и недавно, когда узнал, что строго доказана связь степени сжатия данных с их энтропией Колмогорова-Синая. Интуитивно это понятно — чем более упорядочены данные, тем больше возможностей для сжимающей кодировки.
Однако строгое математическое рассмотрение не всегда подтверждает «здравый смысл»;
и хотя статьи на эту тему довольно заковыристые (а основная — ещё и платная), поверим теоретикам, что всё законно и приступим к опытам.
Создадим данные 4-х видов:
- десятичные цифры числа Пи (π)
- ГПСЧ Wolfram Mathematica (Random)
- самый яркий и простой образец детерминированного хаоса — логистическое отображение (Logistic)
- массив из одних «1» (Const)
- некая глюковатая формула, генерирующая на первый взгляд случайные числа (Map)
Разумеется, мы можем вычислить энтропии по формуле Шеннона (встроена в Mathematica как Entropy[]).
Однако, как и говорилось выше, результат будет сильно зависеть от системы счисления, формы представления данных и т.п.
Вот, например, график энтропий логистического для всё увеличивающегося объёма данных:

Не очень понятно, стремится ли энтропия к определённому значению при увеличении размера массива.
А теперь попробуем мерить энтропию с помощью сжатия. Для каждого примера наделаем массивы разных размеров и построим графики отношений «размер после сжатия/размер до сжатия» в зависимости от длины массива (честно говоря, использовал не вынесенный в заголовок WinRAR, а встроенный zip-архиватор Mathematica)

Вот это уже правильные, «винрарные» картинки! Хорошо видно, как коэффицент сжатия выходит на предельное значение, которое и характеризует меру хаотичности исходных данных.
Напомню, что чем менее упорядоченны данные — тем труднее их кодировать.
Наибольший остаточный объём — у цифр числа Пи и случайных чисел (почти слившиеся синий и красный
графики).
Пример развития идеи.
Вместо «скучных» чисел возьмём осмысленные литературные тексты. Степень их стохастичности и способы сжатия — весьма обширная тема (см. например )
Здесь мы просто убедимся, что измерения с помощью архиваторов также имеют смысл.
В качестве примеров взяты примерно равные отрывки русских сказок, духовных бесед Джидду Кришнамурти и речей Л.И. Брежнева.

Интересно получилось — для малых отрывков степень сжатия (т.е. упорядоченность) текстов заметно отличается, при этом лидирует Брежнев(!) Но для больших массивов энтропия текстов примерно одинакова.Что сие означает и всегда ли так — неизвестно.
ссылка на оригинал статьи http://habrahabr.ru/post/180803/
Добавить комментарий