 В этой статье я расскажу об одном необычном подходе к генерации лабиринтов. Он основан на модели Амари́ нейронной активности коры головного мозга, являющейся непрерывным аналогом нейронных сетей. При определенных условиях она позволяет создавать красивые лабиринты очень сложной формы, подобные тому, что приведен на картинке.
В этой статье я расскажу об одном необычном подходе к генерации лабиринтов. Он основан на модели Амари́ нейронной активности коры головного мозга, являющейся непрерывным аналогом нейронных сетей. При определенных условиях она позволяет создавать красивые лабиринты очень сложной формы, подобные тому, что приведен на картинке.
Вас ждет много анализа и немного частных производных. Код прилагается.
Прошу под кат!
Введение
Многие из читателей уже сталкивались с задачей генерации лабиринта в той или иной форме и знают, что для ее решения зачастую используют алгоритмы Прима и Крускала нахождения минимального остовного дерева в графе, вершины которого являются ячейками лабиринта, а ребра представляют проходы между соседними ячейками. Мы же сделаем смелый шаг прочь от теории графов в сторону… вычислительной нейробиологии.
В течение XX века ученые строили математические модели одиночных нейронов (клеток нервной системы) и их взаимодействия между собой. В 1975 году С. Амари представил свету свою непрерывную модель коры головного мозга. В ней нервная система рассматривалась как сплошная среда, в каждой точке которой находится «нейрон», характеризуемый значением потенциала своей мембраны, которая меняет свой потенциал, обмениваясь зарядами с соседними нейронами и внешними раздражителями. Модель Амари знаменита тем, что объясняет многие феномены человеческого зрения и, в частности, зрительные галлюцинации, вызываемые психоактивными веществами.
Модель Амари, в ее простейшем виде, представляет собой задачу Коши для одного интегро-дифференциального уравнения:
Здесь не обойтись без пояснений:
 — вещественное значение потенциала мембраны нейрона в точке
— вещественное значение потенциала мембраны нейрона в точке  в момент времени
в момент времени  .
.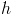 — потенциал покоя (некоторая вещественная константа).
— потенциал покоя (некоторая вещественная константа).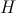 — ступенчатая функция Хэвисайда:
— ступенчатая функция Хэвисайда:

 — весовая функция.
— весовая функция. — внешний раздражитель.
— внешний раздражитель. — распределение потенциала в начальный момент времени.
— распределение потенциала в начальный момент времени. — произвольная точка области
— произвольная точка области  , на которой определен потенциал. Поскольку мы планируем генерировать двумерное изображение лабиринта, в качестве
, на которой определен потенциал. Поскольку мы планируем генерировать двумерное изображение лабиринта, в качестве  будем рассматривать всю вещественную плоскость.
будем рассматривать всю вещественную плоскость.- Частная производная
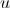 по времени в левой части обозначает мгновенное изменение потенциала
по времени в левой части обозначает мгновенное изменение потенциала 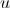 . Правая часть задает правило этого изменения.
. Правая часть задает правило этого изменения. - Первые два слагаемых правой части означают, что при отсутствии раздражителей значение потенциала стремится к значению потенциала покоя.
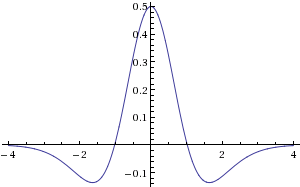
- Следующее слагаемое учитывает воздействие соседних нейронов. Функция Хэвисайда играет роль активационной функции нейрона: нейрон начинает влиять на соседей лишь при условии, что его потенциал больше нуля. Будем далее называть такие нейроны активными, а множество точек с положительным потенциалом — областью активности. Ясно, что покоящиеся нейроны не должны быть активными, то есть потенциал покоя не должен быть положительным. Активных соседей можно условно разделить на две группы: возбуждающие и тормозящие. Возбуждающие нейроны увеличивают потенциал соседей, а тормозящие — уменьшают. При этом возбуждающие создают мощный всплеск активности в малой окрестности, а тормозящие постепенно гасят активность в окрестности большого радиуса. Именно этот факт отражен в выборе весовой функции
 в форме «мексиканской шляпы»:
в форме «мексиканской шляпы»:

- Последнее слагаемое правой части уравнения учитывает действие внешнего раздражителя. Например, для зрительной коры головного мозга естественным раздражителем является сигнал, полученный с сетчатки глаза. Будем считать, что раздражитель задан неотрицательной стационарной (независящей от времени) функцией.
Зададимся вопросом: можно ли подобрать параметры модели 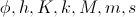 так, чтобы ее стационарное решение (при
так, чтобы ее стационарное решение (при  ) было изображением некоторого лабиринта?
) было изображением некоторого лабиринта?
Свойства решений модели Амари
Для анализа решений модели Амари нам будет достаточно ограничиться рассмотрением одномерного случая. Для простоты будем полагать, что  постоянна на всей прямой.
постоянна на всей прямой.
В первую очередь нас интересуют так называемые бамп-решения. Они замечательны тем, что положительны лишь на некотором конечном интервале  с подвижными границами. Уравнение Амари для них записывается следующим образом:
с подвижными границами. Уравнение Амари для них записывается следующим образом:
Чтобы понять, как ведет себя его решение, введем функцию
Теперь то же уравнение можно переписать так:
Нам известно, что бамп-решение обращается в ноль на границах интервала активности (потому они и называются границами). Запишем это условие на правой границе:
А теперь продифференцируем последнее тождество по переменной  :
:
Отсюда:
Подставляя последнее выражение в уравнение для бамп-решения при 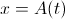 , получим:
, получим:
Теперь заметим, что частная производная по  в левой части всегда отрицательна, так как слева от правой границы решение больше нуля, а справа от нее — меньше. Поэтому
в левой части всегда отрицательна, так как слева от правой границы решение больше нуля, а справа от нее — меньше. Поэтому
Таким образом, направление сдвига границы зависит лишь от значения выражения в правой части. Если оно больше нуля, то область активности расширяется, если меньше — сужается. При равенстве нулю достигается равновесие.
Взглянем на возможные графики функции  .
.
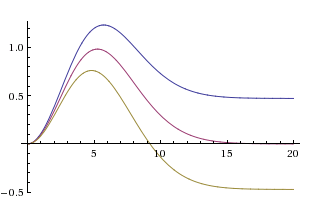
Очевидно, возможны два случая:
- Предельное значение
 неотрицательно. Тогда область активности бамп-решения будет неограниченно расширяться.
неотрицательно. Тогда область активности бамп-решения будет неограниченно расширяться. - Предельное значение
 отрицательно. Тогда область активности будет ограничена. Более того, в этом случае можно показать, что связные компоненты области активности решения уравнения Амари никогда не сливаются.
отрицательно. Тогда область активности будет ограничена. Более того, в этом случае можно показать, что связные компоненты области активности решения уравнения Амари никогда не сливаются.
К сожалению, в двумерном случае получить явное выражение для функции  затруднительно, поэтому мы просто оценим ее:
затруднительно, поэтому мы просто оценим ее:
Отсюда:
Генерация лабиринта
Собрав багаж необходимых знаний, мы можем приступить к, собственно, алгоритму генерации лабиринта.
Прежде всего, определимся с самим понятием «лабиринт». Под лабиринтом будем подразумевать бинарную функцию  такую, что область
такую, что область 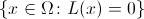 связна. Значение 0 соответствует свободной ячейке, а значение 1 — непроходимой стене. Условие связности говорит о том, что из любой свободной ячейки можно добраться до любой другой, не разрушая стены. Функцию
связна. Значение 0 соответствует свободной ячейке, а значение 1 — непроходимой стене. Условие связности говорит о том, что из любой свободной ячейки можно добраться до любой другой, не разрушая стены. Функцию  будем искать в виде:
будем искать в виде:
где 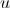 — решение модели Амари. Осталось лишь определиться с параметрами модели.
— решение модели Амари. Осталось лишь определиться с параметрами модели.
Начнем с того, что зафиксируем произвольное отрицательное значение 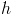 . Естественно положить
. Естественно положить 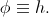 . Теперь зададим функцию
. Теперь зададим функцию  . Пусть ее значение в каждой точке определяется случайной величиной, равномерно распределенной на отрезке
. Пусть ее значение в каждой точке определяется случайной величиной, равномерно распределенной на отрезке  . В таком случае раздражитель не будет создавать активность. Зафиксируем произвольное положительное
. В таком случае раздражитель не будет создавать активность. Зафиксируем произвольное положительное  . Этот параметр влияет лишь на абсолютную величину потенциала, потому не представляет интереса. Зафиксируем произвольные положительные
. Этот параметр влияет лишь на абсолютную величину потенциала, потому не представляет интереса. Зафиксируем произвольные положительные 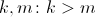 . Они определяют характерную толщину стен лабиринта. Параметр
. Они определяют характерную толщину стен лабиринта. Параметр  попробуем определить экспериментально, а затем сравнить с теоретической оценкой, полученной в предыдущем разделе.
попробуем определить экспериментально, а затем сравнить с теоретической оценкой, полученной в предыдущем разделе.
Стационарное решение будем искать методом последовательных приближений:
А вот и долгожданная интерактивная демонстрация на Python:
import math import numpy import pygame from scipy.misc import imsave from scipy.ndimage.filters import gaussian_filter class AmariModel(object): def __init__(self, size): self.h = -0.1 self.k = 0.05 self.K = 0.125 self.m = 0.025 self.M = 0.065 self.stimulus = -self.h * numpy.random.random(size) self.activity = numpy.zeros(size) + self.h self.excitement = numpy.zeros(size) self.inhibition = numpy.zeros(size) def stimulate(self): self.activity[:, :] = self.activity > 0 sigma = 1 / math.sqrt(2 * self.k) gaussian_filter(self.activity, sigma, 0, self.excitement, "wrap") self.excitement *= self.K * math.pi / self.k sigma = 1 / math.sqrt(2 * self.m) gaussian_filter(self.activity, sigma, 0, self.inhibition, "wrap") self.inhibition *= self.M * math.pi / self.m self.activity[:, :] = self.h self.activity[:, :] += self.excitement self.activity[:, :] -= self.inhibition self.activity[:, :] += self.stimulus class AmariMazeGenerator(object): def __init__(self, size): self.model = AmariModel(size) pygame.init() self.display = pygame.display.set_mode(size, 0) pygame.display.set_caption("Amari Maze Generator") def run(self): pixels = pygame.surfarray.pixels3d(self.display) index = 0 running = True while running: self.model.stimulate() pixels[:, :, :] = (255 * (self.model.activity > 0))[:, :, None] pygame.display.flip() for event in pygame.event.get(): if event.type == pygame.QUIT: running = False elif event.type == pygame.KEYDOWN: if event.key == pygame.K_ESCAPE: running = False elif event.key == pygame.K_s: imsave("{0:04d}.png".format(index), pixels[:, :, 0]) index = index + 1 elif event.type == pygame.MOUSEBUTTONDOWN: position = pygame.mouse.get_pos() self.model.activity[position] = 1 pygame.quit() def main(): generator = AmariMazeGenerator((512, 512)) generator.run() if __name__ == "__main__": main() Я полагаю, что комментарии излишни. Хотелось бы отметить лишь то, что свертка с весовой функцией вычисляется через фильтр Гаусса, причем изображения продолжаются периодически на всю плоскость (параметр «wrap»). Демонстрация интерактивна в том смысле, что позволяет принудительно установить положительный потенциал в любой точке по клику.
Поведение решения, как и ожидалось, зависит от выбора параметра  :
:
 |
 |
 |
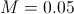 |
 |
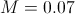 |
Теперь получим теоретическую оценку оптимального значения параметра  . Оно удовлетворяет условию:
. Оно удовлетворяет условию:
Поэтому его можно оценить следующим образом:
Неплохо, однако реальное значение  чуть выше теоретической оценки. В этом легко убедиться, положив
чуть выше теоретической оценки. В этом легко убедиться, положив 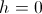 .
.
Наконец, можно менять степень «разреженности» лабиринта, изменяя значение параметра 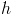 :
:
 |
 |
 |
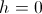 |
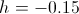 |
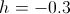 |
Заключение
Вот мы и закончили рассмотрение, пожалуй, самого необыкновенного способа генерации лабиринтов. Надеюсь, что статья показалась Вам интересной. В заключение приведу список литературы для желающих расширить свой кругозор:
[1] Konstantin Doubrovinski, Dynamics, Stability and Bifurcation Phenomena in the Nonlocal Model of Cortical Activity, 2005.
[2] Dequan Jin, Dong Liang, Jigen Peng, Existence and Properties of Stationary Solution of Dynamical Neural Field, 2011.
[3] Stephen Coombes, Helmut Schmidt, Ingo Bojak, Interface Dynamics in Planar Neural Field Models, 2012.
ссылка на оригинал статьи http://habrahabr.ru/post/181265/

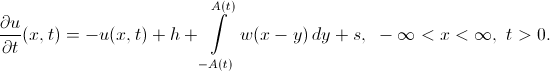

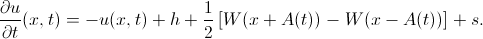
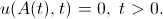
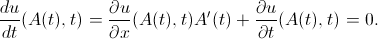
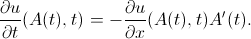




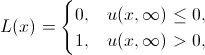
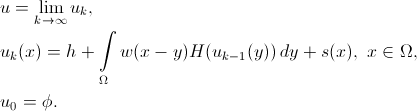


Добавить комментарий