Решил недавно написать симулятор полёта спутника вокруг центрального тела. Сразу оговорюсь, что масса спутника принебрежительно мала, по сравнению с массой центрального тела.


Собственно первой частью работы было изучение математики.Тут было довольно просто: использовались элементарные уравнения кинематики.

/* t - время шага G - коэффициент притяжения(аналог гравитационной постоянной) msun - масса центрально объекта (в условных еденицах) */ var r2=(xsun-xc)*(xsun-xc)+(ysun-yc)*(ysun-yc); //  Квадрат радиуса-вектора var gs=G*msun/r2;       // Ускорение, сообщаемое спутнику // Разложение пройденного пути по векторам                                   var ivx=(t*t*gs/2)*(xsun-xc)/Math.sqrt(r2);             var ivy=(t*t*gs/2)*(ysun-yc)/Math.sqrt(r2); // прибавление средней арифметической скорости vx+=ivx/t;                                                vy+=ivy/t; var V=Math.sqrt(vx*vx+vy*vy)                                   // модуль скорости  /* Координаты */ xc+=vx*t; yc+=vy*t; 

Собственно на этом математическая часть закончилась.

Интерфейс

По задумке планировалось, что пользователь сам выберет начальную точку и сам сообщит начальную скорость.
Реализовывал на JS через два слушателя событий:

var xc,yc,xc2,yc2,intervalID,vx,vy; /* Кнопка нажата */ cnv.addEventListener('mousedown',function (event) { /* получаем начальное положение спутника */ xc=event.offsetX; yc=event.offsetY;  /*  На всякий случай очищаем анимацию */ clearInterval(intervalID) }, false) /* В это время юзер переносит мышь, задавая направление и модуль начальной скорости */ cnv.addEventListener('mouseup',function (event) { /*  И тут тоже очищаем анимацию */ clearInterval(intervalID) /* получаем координаты мыши */ xc2=event.offsetX; yc2=event.offsetY; /* разложение скорости по векторам*/ vx=(-xc+xc2)*0.4 /* начинаем анимацию*/ vy=(-yc+yc2)*0.4 intervalID=setInterval(dodo,70); }, false) 

Тестирование

Первое тестирование было довольно инетересным для меня, как для астронома))
Если орбита была очень эллиптична, то она вот так прецесировала:

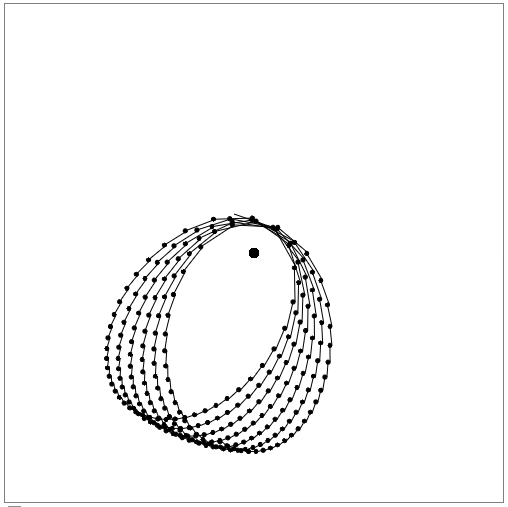
С одной стороны было приятно смотреть на такое явление, а с другой, я понимал что дело здесь не в прецесии, а в неточности вычисления положения, ведь иногда были и такие орбиты:

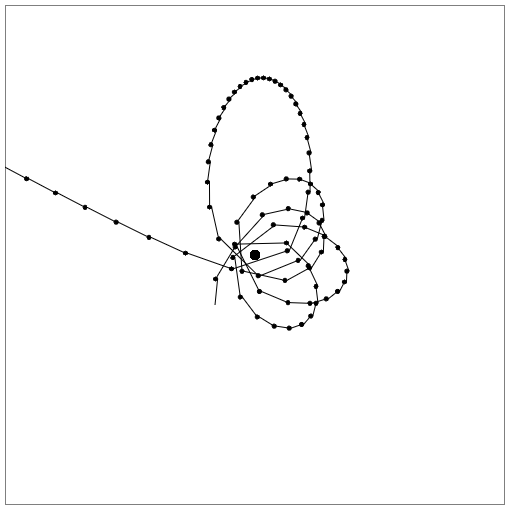
На самом деле проблема оказалась проста: в идеале анимация должна быть дифференцирована по времени, то есть разбита на настолько малые временные шаги, что скорость, и её направление не успевали сильно измениться. А мы поставили постоянный шаг времени, и если этого шага было вполне достаточно для вычисления положения спутника в афелии, то в перегелии он должен быть в разы меньше. Для этого и был сделан плавающий шаг вычисления положения, в то время как шаг отрисовки остался постоянным.
Реализация:

var i=0; do{ var r2=(xsun-xc)*(xsun-xc)+(ysun-yc)*(ysun-yc); var gs=G*msun/r2; var ivx=(t*t*gs/2)*(xsun-xc)/Math.sqrt(r2); var ivy=(t*t*gs/2)*(ysun-yc)/Math.sqrt(r2); vx+=ivx/t; vy+=ivy/t; var V=Math.sqrt(vx*vx+vy*vy) xc+=vx*t; yc+=vy*t; i++ }while(i<=1/t) 

Доводка

Для доводки сделал радиус-вектор спутника, который помогает понять где он находиться, когда спутник улетел из картинки:

ctx.moveTo(xc,yc) ctx.lineTo(xsun,ysun) ctx.stroke() 

Находиться всё здесь: http://astrokot.ru/planetarium/vectors.html