
В прошедшее воскресенье состоялся 3-й, заключительный квалификационный раунд Russian Code Cup. Все, кто хотел принять участие, смогли прийти и побороться за место в отборочном раунде.
Напомним, что чемпионат Russian Code Cup состоит из нескольких онлайн-туров, по результатам которых выбираются финалисты для заключительного соревнования, в оффлайне.
Всего проходит 3 квалификационных раунда, в каждом из которых определяется 200 победителей. Иногда в отборочный раунд проходит 201 человек. Это связано с тем, что последние места поровну делят несколько участников, набравшие равное количество баллов.
В отборочном раунде участвуют победители квалификационных раундов. В сумме получается 600 человек (или 603, если в квалификационные раунды прошли по 201 человеку). После отборочного раунда определяются 50 финалистов. В данном случае также может сложиться ситуация, когда последнее место разделят двое участников. В таком случае в финал пройдет 51 человек.
До отборочного раунда остаётся около двух недель. В ожидании следующего тура подведём итоги последнего квалификационного раунда и разберём задачи.
Темы задач:
- Задача A. Экзамен.
- Задача B. Сообщение.
- Задача C. Матч века.
- Задача D. Разбиение на массивы.
- Задача E. Лесной феномен.
За время раунда авторизовался 681 человек. Из них хотя бы одно решение прислали 529 человек.
Всего было отправлено 2660 решений.
Участники, первыми приславшие решения соответствующих задач, и время после начала раунда (мин: сек):
- Задача А: Irinka (3:59)
- Задача B: arch (5:18)
- Задача C: mr146 (19:53)
- Задача D: megaterik (37:26)
- Задача E: peter50216 (78:11)
За время проведения раунда были замечены два списывальщика. Их результаты были аннулированы сразу же по окончании раунда. Списывальщиков выявляет специальный алгоритм, разработанный специалистами ИТМО и интегрированный в систему проверки заданий.
Территориальное распределение участников в этом раунде было следующим:
Россия => 337
Украина => 81
Беларусь => 42
Казахстан => 18
Армения => 10
США => 9
Узбекистан => 4
Швейцария => 4
Грузия => 3
Болгария => 2
Латвия => 2
Швеция => 2
Германия => 2
Исландия => 1
Туркменистан => 1
Республика Корея => 1
Ирландия => 1
Македония => 1
Азербайджан => 1
Румыния => 1
Испания => 1
Великобритания => 1
Франция => 1
Молдова => 1
Кыргызстан => 1
Польша => 1
Сербия => 1
В отборочный тур вышло 200 человек. Первые 10 из них:
- Андрей Максай
- Денис Мухаметьянов
- Участник с ником peter50216
- Виктор Баринов
- Александр Барыкин
- Михаил Ройзнер
- Максим Калинин
- Роман Едемский
- Игорь Киров
- Андрей Заякин
Разбор задач, который мы приводим ниже, также доступен на сайте Russian Code Cup.
Задача А. Экзамен
Идея: Николай Ведерников
Реализация: Николай Ведерников
Разбор: Николай Ведерников
Условие задачи
Ограничение по времени: 2 секунды
Ограничение по памяти: 256 мегабайт
Игорь — хороший программист, но большой разгильдяй. Проиграв весь семестр в компьютерные игры и просмотрев очень много сериалов и фильмов, он неожиданно понял, что пришло время сессии, которую надо закрывать, чтобы не вылететь из университета.
Первым у Игоря будет экзамен по экстремальному программированию. Суть экзамена заключается в том, что в некоторое время S появляется условие задачи, которую Игорь должен решить до момента времени F. Экзамен длится не менее секунды и не более суток. Если Игорь сдает задачу за отведенное время, то он сдает экзамен. Если он успеет сдать задачу в течение часа после окончания экзамена, то помимо решения задачи ему приходится писать тестирование. Иначе Игорь заваливает экзамен.
Игорь знает, за сколько минут напишет программу, и теперь хочет узнать, сможет ли он сдать экзамен, либо ему придётся писать тест, либо он вообще экзамен не сдаст.
| Формат входных данных | Первая строка входных данных содержит единственное целое число n(1 ≤ n ≤ 104) — количество тестов. Следующие n строк содержат S и F в формате hh:mm:ss, а также целое число k (1 ≤ k ≤ 2000) — время начала и конца экзамена и время в минутах, за которое Игорь напишет программу. Гарантируется, что время в тестах задано корректно. |
||||
| Формат выходных данных | Для каждого теста в отдельной строке выведите ответ на задачу. Если Игорь сдаст экзамен, то выведите Perfect. Если Игорю придётся писать тест, то выведите Test. Иначе выведите Fail. | ||||
| Примеры |
|
Разбор задачи
Переведем время начала и конца экзамена в секунды по формуле 60 × 60 × hh + 60 × mm + ss, а также время, которое потратит Игорь на написание программы, по формуле 60 × k. Затем вычислим длину экзамена по формуле timeexam = (timeend — timestart + 24 × 60 × 60) % (24 × 60 × 60), если же timeexam = 0, то на самом деле длина экзамена 24 × 60 × 60. Если время написания программы меньше продолжительности экзамена, то ответ Perfect. Если время написания экзамена меньше чем продолжительность экзамена, увеличенного на час (60 × 60 секунд), то ответ Test. Иначе ответ Fail.
Задача B. Сообщение
Идея: Павел Кротков
Реализация: Анна Малова
Разбор: Анна Малова
Условие задачи
Ограничение по времени: 2 секунды
Ограничение по памяти: 256 мегабайт
После многих лет безуспешных попыток ученые наконец-то смогли установить связь с разумной цивилизацией в космосе и выяснили, что алфавит инопланетян состоит всего из двух букв: a и b. Для приема сообщений был сконструирован специальный приемник, который выдает символы a, b, а также специальный символ ?, если разобрать, какой символ был передан, не удалось.
Анализ показал, что инопланетяне передают все свои сообщения в виде двух одинаковых записанных подряд строк. Например, строки «abab» или «aaaaaa» могут быть сообщениями инопланетян, а «abba» или «aaa» — нет.
Прибор, сконструированный учеными, получив на вход потенциальное сообщение инопланетян, выдает все возможные способы прочитать строку без учета описанного выше свойства. Например, получив строку «ab??» прибор выдает строки «abaa», «abab», «abba» и «abbb», из них на самом деле только строка «abab» может быть сообщением от инопланетян, а остальные три не могут.
Для улучшения качества прибора ученые хотят узнать, сколько строк из тех, которые выведены прибором, не могут быть сообщением инопланетян. Помогите им это сделать.
| Формат входных данных | В первой строке содержится натуральное число n — число слов в сообщении, полученном учеными. В каждой из следующих n строк содержится слово из сообщения, состоящее из символов a, b и?.. Гарантируется, что все слова имеют четную длину, а также что в каждом слове есть хотя бы один?.. Суммарная длина всех слов не превышает 200000. Не гарантируется, что есть хотя бы один способ расшифровать каждое слово как сообщение инопланетян. |
||||
| Формат выходных данных | Выведите n строк. В i-ой строке выведите число способов заменить? на буквы a, b так, чтобы i-е слово не было корректным сообщением инопланетян. Так как число способов может быть очень большим, необходимо выводить его по модулю 109+7. | ||||
| Примеры |
|
Разбор задачи
Заметим, что ответ равен числу всех возможных сообщений, минус число тандемных повторов. Обозначим за m число вопросов в строке, а за 2l — длину строки. Тогда количество всех возможных сообщений равно 2m. Число тандемных повторов можно найти из следующих рассуждений. Если на позиции i стоит знак вопроса, а на позиции i + la или b, то в тандемном повторе на позиции i должна стоять та же буква. Если же на обеих позициях i и i + l стоят знаки вопроса, то ответ нужно домножить на два. Аналогично рассматривается ситуация, когда знак вопроса стоит на позиции i + l. Если на позициях i и i + l стоят различные буквы, то тандемных повторов для такой строки не существует.
Время работы O(длины сообщения).
Задача C. Матч века
Идея: Виталий Аксенов
Реализация: Павел Кротков
Разбор: Павел Кротков
Условие задачи
Ограничение по времени: 2 секунды
Ограничение по памяти: 256 мегабайт
Каждый год студенты Межгалактического Физкультурно-Теологического Института проводят «матч века» по космическому футболу. Этот матч длится одни световые сутки, и в нем принимают участие игроки сборных всех факультетов института.
Перед тем как начать матч, судье необходимо разделить всех игроков на две команды и присвоить им номера. Всего в матче участвуют 2n игроков, из которых n случайно выбранных игроков судья отправляет в первую команду, а n оставшихся — во вторую. После этого судья присваивает номера всем игрокам обеих команд.
Игроки обеих команд получают номера, каждый из которых является целым числом от 1 до n. Номера всех игроков одной команды попарно различны. Традиционно в первой команде игроки получают номера в порядке убывания их роста, а во второй — в порядке возрастания.
Студенты, видевшие много матчей века, любят высчитывать «зрелищность» каждого матча — сумму попарных разниц роста между игроками разных команд, имеющих одинаковые номера. Так, если в первой команде играют игроки с ростом 180 и 190 сантиметров, а во второй — игроки с ростом 170 и 205 сантиметров, то зрелищность этого матча равна |180 — 205| + |190 — 170| = 45. Теперь им интересно вычислить математическое ожидание зрелищности «матча века», зная рост всех его участников. Помогите им.
Формат входных данных В первой строке входных данных содержится натуральное число t — количество матчей века, которые необходимо изучить. Далее следуют описания самих матчей.
Описание каждого матча состоит из двух строк. Первая строка содержит одно четное натуральное число 2n — количество участников очередного «матча века». Следующая строка содержит 2n попарно различных натуральных чисел, не превышающих 106 — рост всех участников.
Суммарное количество участников во всех матчах, которые необходимо изучить, не превышает 106.
| Формат входных данных | В первой строке входных данных содержится натуральное число t — количество матчей века, которые необходимо изучить. Далее следуют описания самих матчей. Описание каждого матча состоит из двух строк. Первая строка содержит одно четное натуральное число 2n — количество участников очередного «матча века». Следующая строка содержит 2n попарно различных натуральных чисел, не превышающих 106 — рост всех участников. Суммарное количество участников во всех матчах, которые необходимо изучить, не превышает 106 |
||||
| Формат выходных данных | Для каждого матча в отдельной строке выведите одно вещественное число — искомое математическое ожидание. Ваш ответ должен отличаться от правильного не более чем на 10-6 | ||||
| Примеры |
|
Разбор задачи
Пусть в матче участвуют 2 × n игроков. Пронумеруем их в порядке возрастания роста. Теперь докажем следующее утверждение: искомая сумма одинакова при любом разбиении по командам, и равна an + 1 + an + 2 +… + a2 × n — a1 — a2 — … — an. Переформулируем: рост любого игрока, номер которого не превышает n, всегда входит в искомую сумму со знаком минус, а рост игрока, номер которого больше n, входит в искомую сумму с плюсом.
Доказывать утверждение будем по индукции. Очевидно, что оно выполняется для случая с n = 1. Теперь докажем справедливость утверждения для произвольного n при условии справедливости для n — 1. Посмотрим на то, в какую команду попал игрок с наименьшим ростом. Если он оказался в первой команде, он получит в ней номер n. Заметим, что игрок второй команды, получивший тот же номер, окажется, как минимум, (n + 1)-м по росту среди всех игроков матча. Выкинем из состава этих игроков, после чего задача сведется к меньшей. Случай, в котором игрок с наименьшим ростом попал во вторую команду, рассматривается аналогично.
После доказательства этого утверждения, решение задачи становится очевидным. Можно, например, за O(n×log2n) отсортировать всех игроков по росту, после чего учесть первых n с минусом, а остальных — с плюсом.
Задача D. Разбиение на массивы
Идея: Виталий Аксенов
Реализация: Артем Васильев
Разбор: Артем Васильев
Условие задачи
Ограничение по времени: 2 секунды
Ограничение по памяти: 256 мегабайт
Рассмотрим множество целых чисел от 1 до 3n. Необходимо распределить эти числа в три массива a, b и c длиной n так, чтобы для любого i от 1 до n выполнялось следующее: ai + bi = ci
| Формат входных данных | Единственная строка содержит целое число n (1 ≤ n ≤ 23). | ||||||
| Формат выходных данных | Если решения не существует, то в первой строке выведите единственное число −1. В ином случае, выведите 3 строки, в каждой по n целых чисел, разделенных пробелами. В первой строке должны находиться элементы массива a, во второй — элементы массива b, в третьей — массива c. Каждое число от 1 до 3n должно быть выведено ровно один раз. | ||||||
| Примеры |
|
Разбор задачи
Основная идея решения — предподсчет и перебор с отсечениями. Для начала выясним, для каких значений n ответ не существует. Сумма всех чисел от 1 до 3n равна 3n*(3n+1)/2. С другой стороны, обозначим сумму элементов массива с за S. Тогда сумма элементов в массивах а и b также равна S. Получаем, что 2S = 3n*(3n+1)/2, то есть 3n*(3n+1)/2 должно делиться на 4, что выполняется тогда и только тогда, когда n сравнимо с 0 или 1 по модулю 4. В тех случаях, когда остаток от деления n на 4 равен 2 или 3, решения гарантированно не существует. При заданных в условии ограничениях для всех остальных n решение существует.
Для ускорения перебора следует применить эвристики и отсечения. В авторском решении используется то, что при заданных ограничениях, если существует решение, то существует решение, в котором массив a заполнен числами от 1 до n. С данной эвристикой авторское решение способно находить ответ за 3 секунды для всех n от 1 до 36.
Задача E. Лесной феномен
Идея: Виталий Демьянюк
Реализация: Виталий Демьянюк
Разбор: Виталий Демьянюк
Условие задачи
Ограничение по времени: 2 секунды
Ограничение по памяти: 256 мегабайт
Байтландия — очень зеленая и экологичная страна с множеством лесов, рек и озер. Все леса в Байтландии имеют форму идеального прямоугольника. Длины сторон i-го леса равны ni и mi километрам. Каждый лес разделен линиями, параллельными сторонам прямоугольника, на квадраты с длиной стороны равной одному километру. В каждом квадрате живет свой лесник.
Как известно, осенью каждый лесник заготавливает себе дрова на зиму. Но этой осенью произошло что-то невообразимое. По неизвестной причине после заготовки дров каждый лесник бесплатно отгрузил весь свой запас древесины случайному, равновероятно выбранному соседу. Все лесники отгружали дрова одновременно. Два лесника называются соседями, если квадраты леса, в которых они живут, имеют общую сторону.
С целью более детального изучения этого феномена человеческого поведения для каждого леса вам необходимо подсчитать математическое ожидание количества лесников, у которых после этой процедуры оказались хотя бы какие-нибудь дрова на зиму.
| Формат входных данных | В первой строке содержится натуральное число t — количество лесов в Байтландии. В каждой из следующих t строк содержатся по два числа ni и mi — длины сторон i-го леса. (1 ≤ ni ≤ 107, 1 ≤ mi ≤ 107 nm ≥ 2). Количество лесов в Байтландии не превышает 10000. |
||||
| Формат выходных данных | Для каждого леса в отдельной строке выведите искомое математическое ожидание в виде несократимой дроби. Числитель и знаменатель должны быть разделены символом / без дополнительных пробелов. Если знаменатель равен единице, то надо вывести только числитель. | ||||
| Примеры |
|
Разбор задачи
Обозначим один из возможных сценариев раздачи дров x. Определим li,j(x) как функцию, которая равна единице, если у лесника, живущего в квадрате с координатами i и j, есть дрова на зиму, и нулю в противном случае. Количество лесников, у которых есть дрова на зиму, равно сумме li,j(x) по всем квадратам леса. Тогда по линейности математического ожидания, требуемое ожидание равно сумме математических ожиданий li,j по всем квадратам леса. Найдем математическое ожидание li,j: E(li,j) = 0 × pi,j + 1 × (1- pi,j) = 1 — pi,j, где pi,j — вероятность того, что у соответствующего лесника не осталось дров на зиму. Посчитать pi,j можно как произведение вероятностей событий того, что от соответствующего соседа лесник не получил дров.
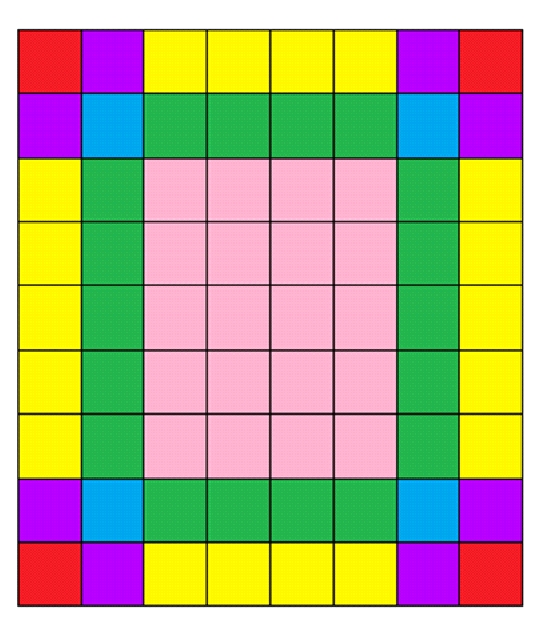
На рисунке выше у квадратов с одинаковым цветом pi,j равны. Поэтому для каждого типа необходимо посчитать количество клеток и умножить его на соотвествующее pi,j, затем все сложить. Время работы программы O(1), так как типов всего шесть. Также нужно отдельно рассмотреть случаи, когда меньшая из сторон равна одному, двум или трем.
Следующий отборочный раунд RCC пройдет 16 июня. Разбор задач обязательно опубликуем. Stay tuned!
ссылка на оригинал статьи http://habrahabr.ru/company/mailru/blog/182256/
Добавить комментарий