Вот некое простое значение:

И мы знаем, как к нему можно применить функцию:

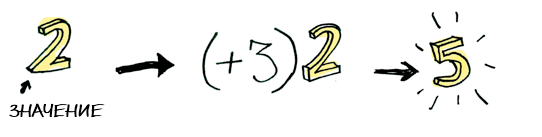
Элементарно. Так что теперь усложним задание — пусть наше значение имеет контекст. Пока что вы можете думать о контексте просто как о ящике, куда можно положить значение:

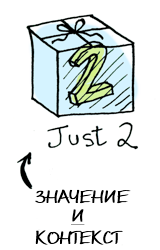
Теперь, когда вы примените функцию к этому значению, результаты вы будете получать разные — в зависимости от контекста. Это основная идея, на которой базируются функторы, аппликативные функторы, монады, стрелки и т.п. Тип данных Maybe определяет два связанных контекста:

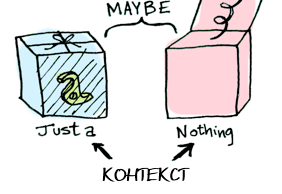
data Maybe a = Nothing | Just a 

Позже мы увидим разницу в поведении функции для Just a против Nothing. Но сначала поговорим о функторах!

Функторы

Когда у вас есть значение, упакованное в контекст, вы не можете просто взять и применить к нему обычную функцию:

И здесь fmap спешит на помощь. fmap — парень с улицы, fmap знает толк в контекстах. Уж он-то в курсе, как применить функцию к упакованному в контекст значению. Допустим, что вы хотите применить (+3) к Just 2. Используйте fmap:

> fmap (+3) (Just 2) Just 5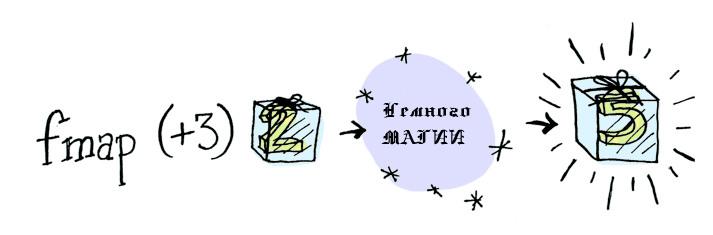 

Бам! fmap продемонстрировал нам, как это делается! Но вот откуда он знает, как правильно применять функцию?

Так что такое функтор на самом деле?

Функтор — это тип классов. Вот его определение:

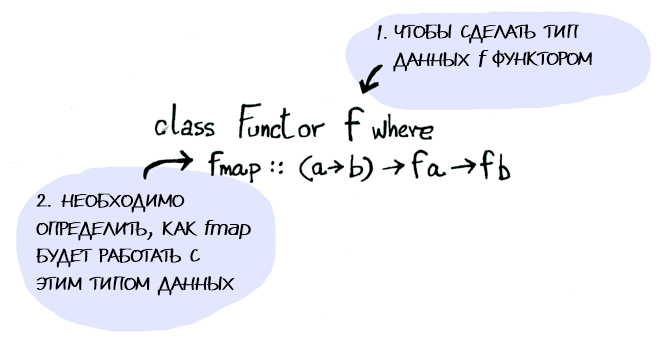
Функтором является любой тип данных, для которого определено, как к нему применяется fmap. А вот как fmap работает:

Так что мы можем делать так:

> fmap (+3) (Just 2) Just 5 

И fmap магическим образом применит эту функцию, потому что Maybe является функтором. Для него определено, как применять функции к Just‘ам и Nothing‘ам:

instance Functor Maybe where       fmap func (Just val) = Just (func val)     fmap func Nothing = Nothing 

Вот что происходит за сценой, когда мы пишем fmap (+3) (Just 2):

А потом вы скажете: «Ладно, fmap, а примени-ка, пожалуйста, (+3) к Nothing.»

> fmap (+3) Nothing Nothing 

Билл О’Рейли ничегошеньки не смыслит в функторе Maybe

Как Морфеус в «Матрице», fmap знает, что делать; вы начали с Nothing и закончите тоже с Nothing! Это fmap-дзен. И теперь понятно, для чего вообще существует тип данных Maybe. Вот, например, как бы вы работали с записью в базе данных на языке без Maybe:

post = Post.find_by_id(1) if post   return post.title else   return nil end 

На Haskell же:

fmap (getPostTitle) (findPost 1) 

Если findPost возвращает сообщение, то мы выдаём его заголовок с помощью getPostTitle. Если же он возвращает Nothing, то и мы возвращаем Nothing! Чертовски изящно, а?
<$> — инфиксная версия fmap, так что вместо кода выше вы частенько можете встретить:

getPostTitle <$> (findPost 1) 

А вот ещё один пример: что происходит, когда вы применяете функцию к списку?

Списки тоже функторы! Вот определение:

instance Functor [] where     fmap = map 

Ладно, ладно, ещё один (последний) пример: что случится, когда вы примените функцию к другой функции?

fmap (+3) (+1) 

Вот эта функция:

А вот функция, применённая к другой функции:

Результат — просто ещё одна функция!

> import Control.Applicative > let foo = fmap (+3) (+2) > foo 10 15 

Так что функции — тоже функторы!

instance Functor ((->) r) where       fmap f g = f . g 

И когда вы применяете fmap к функции, то попросту делаете композицию функций!

Аппликативные функторы

Следующий уровень — аппликативные функторы. С ними наше значение по-прежнему упаковано в контекст (так же как с функторами):

Но теперь в контекст упакована и наша функция!

Ага! Давайте-ка вникнем в это. Аппликативные функторы надувательством не занимаются. Control.Applicative определяет <*>, который знает, как применить функцию, упакованную в контекст, к значению, упакованному в контекст:

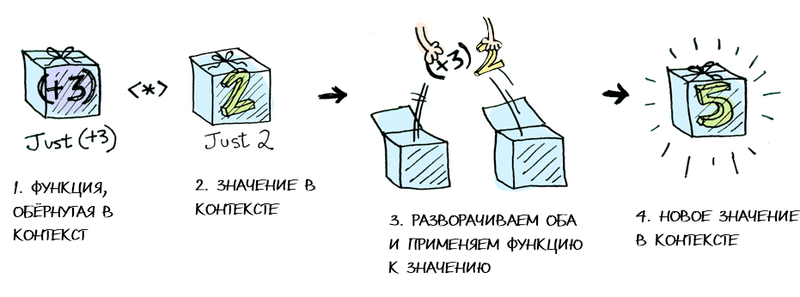
Т.е.

Just (+3) <*> Just 2 == Just 5 

Использование <*> может привести к возникновению интересных ситуаций. Например:

> [(*2), (+3)] <*> [1, 2, 3] [2, 4, 6, 4, 5, 6] 

А вот кое-что, что вы можете сделать с помощью аппликативных функторов, но не сможете с помощью обычных. Как вы примените функцию, которая принимает два аргумента, к двум упакованным значениям?

> (+) <$> (Just 5) Just (+5) > Just (+5) <$> (Just 4) ОШИБКА??? ЧТО ЭТО ВООБЩЕ ЗНАЧИТ ПОЧЕМУ ФУНКЦИЯ УПАКОВАНА В JUST 

Аппликативные функторы:

> (+) <$> (Just 5) Just (+5) > Just (+5) <*> (Just 3) Just 8 

Applicative технично отодвигает Functor в сторону. «Большие парни могут использовать функции с любым количеством аргументов,» — как бы говорит он. — «Вооружённый <$> и <*>, я могу взять любую функцию, которая ожидает любое число неупакованных аргументов. Затем я передам ей все упакованные значения и получу упакованный же результат! БВАХАХАХАХАХА!»

> (*) <$> Just 5 <*> Just 3 Just 15 

Аппликативный функтор наблюдает за тем, как обычный применяет функцию

И да! Существует функция liftA2, которая делает тоже самое:

> liftA2 (*) (Just 5) (Just 3) Just 15 

Монады

Как изучать монады:

1. Получить корочки PhD в Computer Science
2. Выкинуть их нафиг, потому что при чтении этого раздела они вам не понадобятся!

Монады добавляют новый поворот в наш сюжет.
Функторы применяют обычную функцию к упакованному значению:

Аппликативные функторы применяют упакованную функцию к упакованному же значению:

Монады применяют функцию, которая возвращает упакованное значение, к упакованному значению. У монад есть функция >>= (произносится «связывание» (bind)), позволяющая делать это.
Рассмотрим такой пример: наш старый добрый Maybe — это монада:

Просто болтающаяся монада

Пусть half — функция, которая работает только с чётными числами:

half x = if even x            then Just (x `div` 2)            else Nothing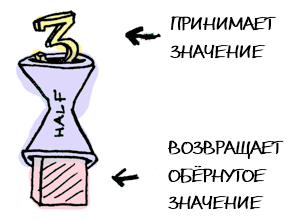 

А что, если мы скормим ей упакованное значение?

Нам нужно использовать >>=, чтобы пропихнуть упакованное значение через функцию. Вот фото >>=:

А вот как она работает:

> Just 3 >>= half Nothing > Just 4 >>= half Just 2 > Nothing >>= half Nothing 

Что же происходит внутри? Monad — ещё один класс типов. Вот его частичное определение:

class Monad m where         (>>=) :: m a -> (a -> m b) -> m b 

Где >>=:

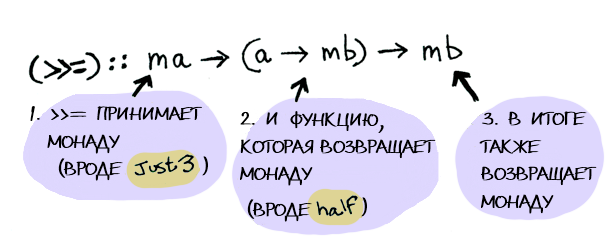
Так что Maybe — это монада:

instance Monad Maybe where     Nothing >>= func = Nothing     Just val >>= func  = func val 

А вот какие действия проделываются над бедным Just 3!

Если же вы подадите на вход Nothing, то всё ещё проще:

Можно так же связать цепочку из вызовов:

> Just 20 >>= half >>= half >>= half Nothing 

Клёвая штука! И теперь мы знаем, что Maybe — это Functor, Applicative и Monad в одном лице.
А сейчас давайте переключимся на другой пример: IO монаду:

В частности, на три её функции. getLine не принимает аргументов и получает пользовательские данные с входа:

getLine :: IO String 

readFile принимает строку (имя файла) и возвращает его содержимое:

readFile :: FilePath -> IO String 

putStrLn принимает строку и печатает её:

putStrLn :: String -> IO () 

Все три функции принимают регулярные значения (или вообще не принимают значений) и возвращают упакованные значения. Значит, мы можем связать их в цепочку с помощью >>=!

getLine >>= readFile >>= putStrLn 

О да, у нас билеты в первый ряд на «Монады-шоу»!
Haskell так же предоставляет нам некоторый синтаксический сахар для монад, называемый do-нотацией:

foo = do     filename <- getLine     contents <- readFile filename     putStrLn contents 

Заключение

1. Функтор — это тип данных, реализуемый с помощью класса типов Functor
2. Аппликативный функтор — это тип данных, реализуемый с помощью класса типов Applicative
3. Монада — это тип данных, реализуемый с помощью класса типов Monad
4. Maybe реализуется с помощью всех трёх классов типов, поэтому является функтором, аппликативным функтором и монадой одновременно

В чём разница между этими тремя?

• функтор: вы применяете функцию к упакованному значению, используя fmap или <$>
• аппликативный функтор: вы применяете упакованную функцию к упакованному значению, используя <*> или liftA
• монада: вы применяете функцию, возвращающую упакованное значение, к упакованному значению, используя >>= или liftM

Итак, дорогие друзья (а я надеюсь, что к этому моменту мы стали друзьями), я думаю, все мы согласимся с тем, что монады простая и УМНАЯ ИДЕЯ (тм). А теперь, после того, как мы промочили горло этим руководством, то почему бы не позвать Мела Гибсона и не допить бутылку до дна? Проверьте раздел, посвящённый монадам, в LYAH. Там очень много вещей, о которых я умолчал, потому что Миран проделал великолепную работу по углублению в этот материал.
Ещё больше монад и картинок можно найти в трёх полезных монадах.

От переводчика:
Ссылка на оригинал: http://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html Пишу её так, потому что Хабр ругается на url с запятыми.
И, конечно, я буду очень признательна за замечания в личку относительно перевода.