Когда я стал постарше, мне захотелось вывести такие же узоры уже на экран компьютера. Долго я думал, как это сделать, по какой формуле рисовать. А пока я думал, формулу эту вывели без меня и даже поместили ее в Википедии — рисуй не хочу. Основная идея вывода там в том, что маленький круг ездит по большому без проскальзывания, а, следовательно, расстояние, пройденное точкой с малого круга, должно равняться соответствующему расстоянию на большом круге.
Однако взятые крепости уже не манят. Естественно теперь задачу обобщить — например, сделать, чтобы маленький круг ездил внутри не окружности, а фигуры посложнее, допустим, эллипса.
Но тут-то резко выясняется, что вывод из Википедии заточен именно под окружность. А для других фигур мы тут же натыкаемся на три препятствия.
Во-первых, окружность — фигура простая и посчитать ее длину очень легко: умножил угол поворота на радиус, и готово. Но длина эллипса, не говоря уже о чем-то сложнее, — это интеграл специального вида, которому даже присвоено собственное название «эллиптической функции». И интеграл этот неберущийся — то есть в элементарных функциях не выражается. А считать длину эллипса через производные, да еще учитывая, что формула там параметрическая — удовольствие небольшое. То есть, запрограммировать, конечно, можно, но вычисления выполняются очень и очень долго.
Во-вторых, окружность — фигура постоянной кривизны. Поэтому прямая между точкой касания кругов и центром большого круга всегда заодно проходит и через маленький круг, что упрощает вывод формул. В случае эллипса (и любой другой кривой с меняющейся кривизной) эти точки разъезжаются в разные стороны как корова на льду. Вот иллюстрация.
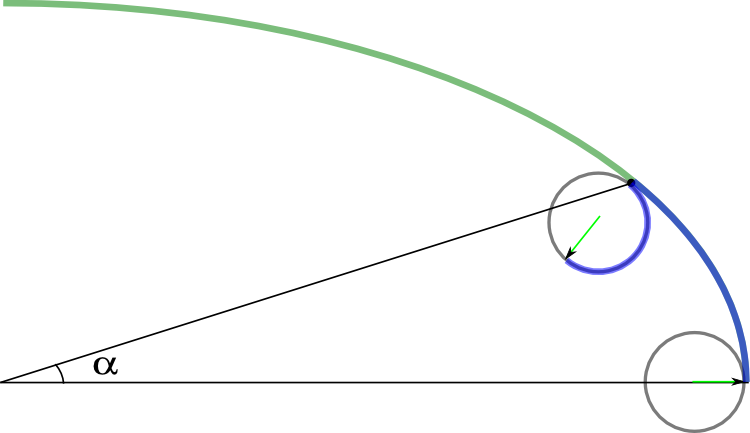
О третьей проблеме будет сказано чуть позже.
Но разум преодолевает все препятствия. Ну или почти все. Если взять из Википедии основную идею равенства пройденного пути и вторую идею -считать расположение дырочки в шестеренке как сумму расположения центра малого круга относительно большого и расположения дырочки относительно малого круга, то после некоторого количества проб и ошибок можно придумать алгоритм рисования.
Итак, снова посмотрите на иллюстрацию вверху. Центр декартовых и полярных координат (нам придется пользоваться и теми, и другими) находится в одном месте — середине основного эллипса, полярные углы мы отмеряем против часовой стрелки от оси x. На маленьком круге специально для красоты нарисовали зеленую стрелочку. Первоначально, при угле 0, малый круг стоит так, что эта стрелка находится под углом в 0, а точка касания его с большим кругом находится на оси x.
Теперь колесико провернули так, что точка касания переместилась в точку, которая находится под углом α, если смотреть из начала координат. За это время конец стрелки прошел некоторый путь, и этот путь равен соответствующему пути на эллипсе (на рисунке оба отмечены синим).
Приблизим немного место действия.
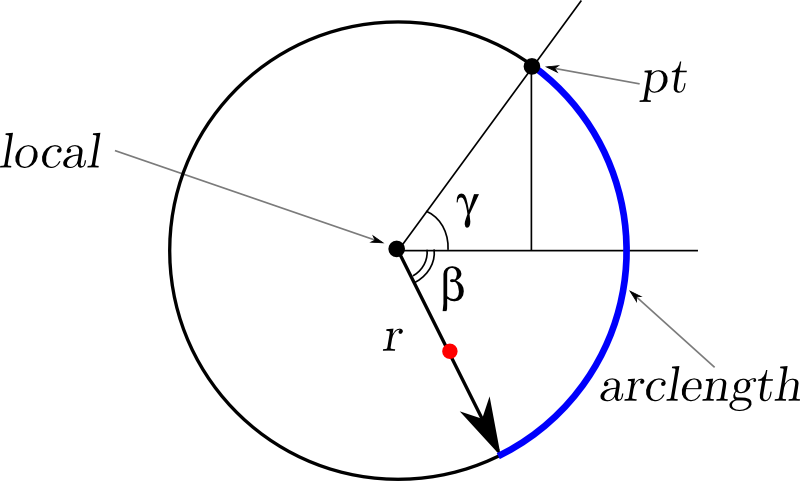
Здесь мы видим все ту же точку касания (обозначена как pt), стрелку на колесике (нарисована жирно), путь, пройденный концом этой стрелки (выделен синим), а заодно и дырочку в колесике (красная точка). local — это центр колесика, в этой точке будет размещаться центр локальной системы координат, с помощью которой мы высчитаем положение дырочки.
Итак, точка pt видна из центра эллипса под углом α. Несложно найти координаты этой точки — как пересечение эллипса и соответствующей прямой. Теперь неплохо бы узнать координаты центра колесика, но для этого нам нужно знать угол γ — направление от центра колесика до точки касания. О! — ключевое слово «касание». В точке касания кривых к ним можно провести общую касательную, а нужный нам угол будет перпендикулярен углу этой касательной. Тангенс угла касательной — это производная эллипса в точке. Осталось всего-то навсего высчитать эту производную.
Конечно, можно взять параметрическое уравнение эллипса и получить от него формулу производной. Но это страшно неудобно — параметр никак не соотносится ни с одной известной нам величиной. А если мы заменим эллипс на что-нибудь другое?
Физики шутят, что господь бог имеет то важное преимущество, что может интегрировать вживую, прямо на физических телах. Вот этим методом мы и воспользуемся.
Что такое производная? Если по-простому, по-колхозному, исключив предельный переход, то это отношение изменения значения функции и изменению значения переменной. Поскольку мы программируем на компьютере, то никаких бесконечностей, подразумеваемых предельным переходом, у нас нет, наш мир дискретен, и для нас такая формула вполне подходит. Поэтому нам только и нужно, что запоминать предыдущую точку и высчитывать соотношение (Ypt-Yprev)/(Xpt-Xprev). Чем более часто мы будем брать точки, тем точнее будут наши расчеты и в конце концов никто от настоящей производной их вообще не отличит.
Ну дальше просто — находим угол γ и по нему координаты центра колесика.
Как теперь найти координаты дырочки в локальных координатах? Все, что надо для этого знать, — это на какой угол β провернулось колесико. Прямо его не высчитаешь, но он равен углу между точкой касания и концом стрелки, из которого вычли уже известный нам угол γ (см. картинку). Надо только не забыть взять потом результат с обратным знаком, потому что наше колесико крутится по часовой стрелки, а углы меряются против часовой.
Как же найти большой угол? Не так сложно — надо всего лишь разделить длину синей дуги на радиус колесика. А длина синей дуги равна соответствующей части дуги эллипса.
Ага-ага, тут-то нас и подстерегают страшные эллиптические функции. Но мы выкрутимся так же, как и с производной — заменим длину кривой длиной ломаной, которая состоит из коротеньких прямых между текущей точкой и предыдущей.
Ну остальное несложно — находим координаты красной точки в локальной системе координат и пересчитываем их в глобальную.
Теперь о третьей проблеме. В википедии задают радиусы большого и малого круга и предсказывают, что если их отношение рационально, то кривая обязательно замкнется (а для чего нам незамкнутые кривые? Они не красивые). Мы тоже можем так сделать, но это бесполезно — длина эллипса выражается иррациональным числом, никакого радиуса у нас нет, и кривая с большой вероятностью не замкнется.
Мы сделаем чуть по-другому: зададим, сколько раз по эллипсу проедет колесико, и сколько раз эа это время оно само должно провернуться. По этим данным мы вычислим, какой радиус должно иметь колесико, чтобы кривая все-таки замкнулась. Здесь нам поможет все то же равенство путей.
Теперь, после долгих расчетов мы наконец сможем насладиться художественным результатом. Смотрите, какое няшное:

Желтая окружность на рисунке — это колесико, внешний черный эллипс — тот самый, в котором мы катаемся, желтый эллипс — путь середины колесика.
Кстати сказать, получившийся алгоритм совершенно не зависит ни от каких свойств эллипса, поэтому внешнюю кривую можно менять как угодно, лишь бы она оставалась замкнутой. Можно взять даже… квадрат. Результат — на следующем рисунке. Он не так радует глаз, но тоже ничего. Потом можно будет в Фотошопе отсечь все лишнее.

Красиво, что и говорить. Но поскольку это не рекламный пост, я никак не могу обойти стороной важный недостаток. Все вышеописанное работает, если кривая достаточно гладкая, а колесико небольшое. Если колесико будет сравнимо по величине с самой кривой, то приведенный выше вывод уже не годится. На графике появляются сомнительные зазубрины, поскольку при расчете по алгоритму выходит, что колесико в некоторых местах стоит так, что касается внешней кривой только в одной точке, а соседние его точки оказываются торчащими наружу кривой. Конечно, на физическом спирографе так не получится, но как это исправить — современной науке пока неизвестно. Если у кого есть идеи — прошу подкидывать.
И напоследок для тех, кто цветистой прозе предпочитает суровую речь алгоритмов, текст программы. Написана она на языке Asymptote — отличном средстве программирования машинной графики.
// Фигура, вокруг которой мы будем кататься path base = scale(3,2)*unitcircle; // это просто единичный круг - для тестирования алгоритма; на круге должны получаться те же кривые, что и для обыкновенного спирографа //path base = unitcircle; // а это квадрат - для извращений // path base = (-3,3)--(3,3)--(3,-3)--(-3,-3)--cycle; // относительное расстояние от центра движущегося круга // (0 - центр, -1 - левый край, +1 - правый край) real p = 0.7; import graph; size(600, 600); // нарисовать координатную сетку //xaxis(ticks=Ticks); //yaxis(ticks=Ticks); // оборотов по внешней кривой int m = 9; // оборотов колесика int n = 29; // находим радиус колесика, при котором кривая замкнется real r = arclength(base)*m/2/pi/n; real hole = r*p; draw(base); //////////////////////////////////////////////// // расчет одного оборота по внешней кривой, phase - угол поворота колесика в начале процедуры real revolution(real phase) { pair prev = (500,500); real arclen = 0; real beta; real gamma; for (real alpha = 0; alpha<=2pi; alpha=alpha+0.005) { // находим точку пересечения прямой с углом альфа и внешней кривой real[][] isect = intersections(base, (0,0)--(500*cos(alpha), 500*sin(alpha))); pair pt = point(base, isect[0][0]); if (prev==(500,500)) { gamma = 0; } else { // накапливаем длину внешней кривой arclen += length(pt-prev); // считаем производную, она же тангенс угла наклона касательной pair deriv = pt - prev; // пересчитываем тангенс в угол real g = atan2(deriv.y, deriv.x); // и находим угол перпендикулярной прямой gamma = g - pi/2; } beta = gamma - arclen/r + phase; // координаты дырочки в локальной системе координат pair local = hole*( cos(beta), sin(beta) ); // координаты центра колесика в глобальный системе кооординат pair center = pt - r*( cos(gamma), sin(gamma) ); pair spiro = center + local; draw(center, green); draw(spiro, blue); // запоминаем нынешнюю точку - она будет нужна на следующей итерации prev = pt; } return beta; } //////////////////////////////////// // рисуем исходное положение колесика - для наглядности real[][] isect = intersections(base, (0,0)--(100, 0)); pair first_point = point(base,isect[0][0]); draw(shift(first_point.x-r,0)*scale(r)*unitcircle, yellow); // катаем колесико, учитывая каждый раз угол его поворота в начале итерации real phase = 0; for (int rev=0; rev<m; rev=rev+1) { phase = revolution(phase); } ссылка на оригинал статьи http://habrahabr.ru/post/184466/
Добавить комментарий