Игра «морской бой»: расстановка кораблей

Доброго времени суток, уважаемые! К сожалению, из-за больничного режима, я не мог последний месяц опубликовать своё очередное изыскание на тему игры «Морской бой». Надеюсь, моя заметка окажется для кого-то полезной, и, даже если и будет частичным повторением, то в новой интерпретации.
Итак, сегодня я хотел бы обсудить вопрос расстановки (не оптимальной, а произвольной) кораблей перед боем. Слева вы видите пример результата работы рассматриваемого далее алгоритма: корабли в форме букв «R», «A», «H», «B» расставлены на игровом поле размером 5х15 с несколькими запрещёнными к использованию клетками (помечены зелёным цветом). Заинтересовавшихся прошу под кат.

Отмечу, что генерация расстановки актуальна не только для искусственного соперника, но и для человека: для создания относительно равных стратегических условий, корабли живого игрока надо расставлять псевдослучайно. В данной статье, рассматривается алгоритм который гарантировано найдёт валидную расстановку (затратив на это конечное время, верхнюю оценку которого можно получить), если она существует (соответственно, может охарактеризовать принципиальную возможность расставить корабли в предложенных условиях).

Количество вариантов

Если рассматривать не классическую эскадру, то общее количество вариантов расстановки кораблей вычисляется по формуле:

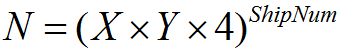
Эта формула учитывает все возможные варианты: даже априорно тупиковые. Необходимость в этой формуле вызвана желанием пронумеровать каждый вариант, чтобы уже потом проверять конкретный номер на приемлемость. Нетрудно заметить, что для 10 кораблей и поля 10х10 мы получаем число порядка 10^26, а это значит, что для индексации нам понадобится переменная размером в 87 бит, с учётом выравнивания – итого больше. Причём увеличение поля, или, что ещё хуже, количества кораблей, усугубляет ситуацию. Так добавление всего одного корабля увеличивает число вариантов до порядка 10^28. Ни один встроенный (аппаратно поддерживаемый) тип данных не подходит для работы с такими числами. Конечно, можно эмулировать арифметику с большими числами, но это обернется потерей производительности и излишне большим вспомогательным инструментарием для одной задачи движка логики игры. Кроме того, использование индексации подразумевает сопоставление каждому индексу уникальной расстановки, то есть индекс всё равно будет «распадаться» на некоторый набор чисел, характеризующий координаты и углы вращения кораблей. Если ещё подумать, то можно обойти проблему больших чисел, используя характер последующего применения индекса.

Перебор вариантов для одного корабля

По сути, мы говорим: тройка чисел характеризует корабль, а набор таких «троек» — эскадру. Упорядочив характеристики, мы можем уточнить: первое число характеризует ординату и изменяется от 0 до (Ymax-1), второе – абсциссу и принадлежит [0; Xmax-1], последнее – угол вращения, принимающий четыре разрешённых состояния. Немного подумав, можно представить себе ключи, характеризующие позицию и вращение корабля в виде дерева Ордината-Абсцисса-Угол (одна палуба помечена для упрощения восприятия; рабочая область – поле 2х2):

Поиск в глубину по такому дереву будет возвращать значения {000}, {001}, {002}, {003}, {010}, {011}, {012} … {113}. Нетрудно заметить, что перечисление ключей напоминает перечисление чисел позиционной системы счисления, в которой каждый разряд имеет свой диапазон значений. Так как каждый разряд нашей системы независим и характеризует одну из степеней свободы корабля, то алгоритм генерации ключей можно представить в виде следующей виртуальной машины:

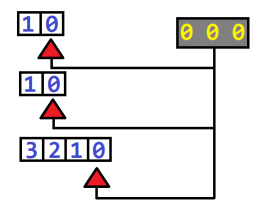
Двигая нижнюю рейку, мы последовательно получим ключи: {000}, {001}, {002} и {003}, после чего рейка «закончится». После исчерпания младшего разряда, возвращаем его рейку в начальное состояние и сдвигаем среднюю на одну позицию. Генератор возвращает {010}, {011}, {012} и {013} – младший и средний разряд исчерпываются. «Сбрасываем» состояние всех исчерпавшихся разрядов, и сдвигаем верхнюю рейку на одну позицию: {100}, {101}, {102} и {103}.
Таким образом, алгоритм запроса очередного ключа следующий:

Перебор вариантов для эскадры

Разобравшись с одним кораблём, мы можем чуть абстрагироваться, и решить задачу для эскадры. Принцип генерации ключей тот же самый, только вместо реек теперь уже выступают генераторы, рассмотренные выше. Мы последовательно перебираем все значения младшего разряда (т.е. здесь – младшего генератора) до его переполнения, затем «увеличиваем следующий за ним разряд на единицу» (то есть запрашиваем новое значение с соответствующего генератора) и вновь прокручиваем младший:
{{000},{000}}
{{000},{001}}
{{000},{002}}
{{000},{003}}
{{000},{010}}
…
{{000},{113}}
{{001},{000}}
…
{{113},{113}}

Генерация расстановки

Итак, наконец-то мы решили первую задачу: мы можем последовательно перебрать все возможные расстановки. Теперь рассмотрим вопрос валидации варианта.
Алгоритм прост: получаем ключ для первого корабля, если поместить корабль возможно – устанавливаем его на поле и переходим к следующему судну, в противном случае – генерируем следующий ключ для данного корабля. Если ключи закончились, подаём сигнал «выше»: для предыдущего корабля подбираем новый валидный ключ, переустанавливаем судно и «возвращаемся». Всё в точности как с цифрами в позиционной системе, только появился ещё ряд ограничивающих правил, запрещающий некоторые сочетания.
Правила можно для удобства разбить по логическим категориям, ускорив, таким образом, проверку за счёт введения обязательных критериев. Например: корабль обязательно должен весь умещаться на игровом поле. Этот простой критерий, применительно к рассмотренному выше случаю, позволит сразу срезать 75% расстановок. Дальнейшие проверки зависят от организации данных в вашей реализации.

Случайности

Всё это хорошо, но детерминированная последовательность действий будет всегда порождать одну и ту же комбинацию, даже если их доступно несколько. Решение просто до безобразия: надо перемешать числа на рейках в генераторах. Просто, считывая i с рейки, возвращайте в точку вызова значение i-ого элемента некоторого массива random_num[i].
В перемешивании элементов массива можно порекомендовать следующее.
Во-первых, формула гарантированно генерирующая индекс второго элемента для обмена, отличный от первого. Вы, конечно, можете не запрещать фиктивный обмен random_num[j]<->random_num[j], но зачем тратить на это итерацию?

//N – количество элементов в массиве //% - остаток целочисленного деления unsigned a_indx=rand()%N; unsigned b_indx=(a_indx+1+rand()%(N-1))%N; //если вы опасаетесь за просадку производительности //из-за дополнительного ‘%’ – его вполне можно //заменить условием

Во-вторых, минимальное достаточное количество для полного перемешивания (беспорядка) выражается как

ceil(N*0.5);

Пример перемешивания чисел на «младшей» рейке и «хороший» генератор приведены далее:

Две итерации обмена привели, в данном случае, к полному перемешиванию. Обратите внимание: данный генератор, как и исходный, вернёт всё множество ключей, но в другом порядке, что позволит от случая к случаю создавать разные расстановки. Отметчу, что «случайность» понятие во многом субъективное, и нетронутые рейки вполне можно считать случайными.

В предыдущих сериях

(прошу прощения, если кого-то забыл упомянуть; сообщите в ЛС)

Заключение

Спасибо всем, кто осилил эту статью, выделив на её прочтение своё время. Постараюсь ответить на возникшие вопросы и прокомментировать критику. Просьба: замечания и советы по корректуре писать в личку, чтобы не уводить обсуждение от предмета статьи.

ссылка на оригинал статьи http://habrahabr.ru/post/186730/