Итак, начнем с того, что первые версии .NET используют алгоритм быстрой сортировки по умолчанию. Поэтому небольшой экскурс в быструю сортировку:
Достоинства:
- Один из самых быстродействующих (на практике) из алгоритмов внутренней сортировки общего назначения;
- Прост в реализации;
- Требует лишь O(logn) дополнительной памяти для своей работы (не улучшенный рекурсивный алгоритм в худшем случае O(n) памяти);
- Хорошо сочетается с механизмами кэширования и виртуальной памяти.
Недостатки:
- Сильно деградирует по скорости до O(n2) при неудачных выборах опорных элементов, что может случиться при неудачных входных данных. Этого можно избежать, выбирая опорный элемент случайно, а не фиксированным образом;
- Наивная реализация алгоритма может привести к ошибке переполнения стека, так как ей может потребоваться сделать O(n) вложенных рекурсивных вызовов. В улучшенных реализациях, в которых рекурсивный вызов происходит только для сортировки меньшей из двух частей массива, глубина рекурсии гарантированно не превысит O(logn);
- Неустойчив — если требуется устойчивость, приходится расширять ключ.
Наивная реализация алгоритма быстрой сортировки может выглядеть примерно так:
public void QuickSort(int left, int right) { int l = left; int r = right; int avg = array[(l + r) / 2)]; do { while (array[l] < avg) ++l; while (array[r] > avg) --r; if (l <= r) { if (l < r) { int temp = array[l]; array[l] = array[r]; array[r] = temp; } ++l; --r; } } while (l <= r); if (left < r) QuickSort(left, r); if (l < right) QuickSort(l, right); }
Вышеописанный алгоритм сортировки имеет следующие недостатки:
- Поскольку опорный элемент выбирается как середина массива, то возможен случай, когда это будет всегда максимум, в результате чего массив будет разбиваться на две части длинною n — 1 и 1 и скорость алгоритма деградирует до O(n2);
- При вышеописанных условиях глубина рекурсии достигает O(n), в результате чего при больших n может произойти переполнение программного стека;
- Алгоритм неустойчив, то есть он меняет элементы с одинаковыми значениями. На примере сортировки чисел это ни как не сказывается, но если мы сортируем массив объектов по какому-либо свойству то это существенно, так как в результате нескольких вызовов метода Sort будем получать массив элементы которого отличаются порядком.
Переходим к рассмотрению реализации в .NET.
.NET 1.0
Итак, рассмотрим, что происходит в .NET 1.0. Забегая, вперед скажу, что ничего хорошего мы здесь не увидим, особенно для пользовательских значимых типов… (из-за отсутствия обобщений в частности)
public static void Sort(Array array) { Array.Sort(array, (Array) null, array.GetLowerBound(0), array.Length, (IComparer) null); } public static void Sort(Array keys, Array items, int index, int length, IComparer comparer) { if (length > 1) { if (comparer == Comparer.Default || comparer == null) { if(TrySZSort(array, null, index, index + length - 1)) { return; } } object[] keys1 = keys as object[]; object[] items1 = (object[]) null; if (keys1 != null) items1 = items as object[]; if (keys1 != null && (items == null || items1 != null)) new Array.SorterObjectArray(keys1, items1, comparer).QuickSort(index, index + length - 1); else new Array.SorterGenericArray(keys, items, comparer).QuickSort(index, index + length - 1); } А теперь собственно классы SorterObjectArray и SorterGenericArray:
private class SorterObjectArray { private object[] keys; private object[] items; private IComparer comparer; public SorterObjectArray(object[] keys, object[] items, IComparer comparer) { base..ctor(); if (comparer == null) comparer = (IComparer) Comparer.Default; this.keys = keys; this.items = items; this.comparer = comparer; } public virtual void QuickSort(int left, int right) { do { int left1 = left; int right1 = right; object obj1 = this.keys[left1 + right1 >> 1]; do { while (this.comparer.Compare(this.keys[left1], obj1) < 0) ++left1; while (this.comparer.Compare(obj1, this.keys[right1]) < 0) --right1; } if (left1 <= right1) { if (left1 < right1) { object obj2 = this.keys[left1]; this.keys[left1] = this.keys[right1]; this.keys[right1] = obj2; if (this.items != null) { object obj3 = this.items[left1]; this.items[left1] = this.items[right1]; this.items[right1] = obj3; } } ++left1; --right1; } else break; } while (left1 <= right1); if (right1 - left <= right - left1) { if (left < right1) this.QuickSort(left, right1); left = left1; } else { if (left1 < right) this.QuickSort(left1, right); right = right1; } } while (left < right); } }
private class SorterGenericArray { private Array keys; private Array items; private IComparer comparer; public SorterGenericArray(Array keys, Array items, IComparer comparer) { base..ctor(); if (comparer == null) comparer = (IComparer) Comparer.Default; this.keys = keys; this.items = items; this.comparer = comparer; } public virtual void QuickSort(int left, int right) { do { int num1 = left; int num2 = right; object obj1 = this.keys.GetValue(num1 + num2 >> 1); do { while (this.comparer.Compare(this.keys.GetValue(num1), obj1) < 0) ++num1; while (this.comparer.Compare(obj1, this.keys.GetValue(num2)) < 0) --num2; } if (num1 <= num2) { if (num1 < num2) { object obj2 = this.keys.GetValue(num1); this.keys.SetValue(this.keys.GetValue(num2), num1); this.keys.SetValue(obj2, num2); if (this.items != null) { object obj3 = this.items.GetValue(num1); this.items.SetValue(this.items.GetValue(num2), num1); this.items.SetValue(obj3, num2); } } ++num1; --num2; } else break; } while (num1 <= num2); if (num2 - left <= right - num1) { if (left < num2) this.QuickSort(left, num2); left = num1; } else { if (num1 < right) this.QuickSort(num1, right); right = num2; } } while (left < right); } } Так что же тут происходит? Следующий код
object[] keys1 = keys as object[]; object[] items1 = (object[]) null; if (keys1 != null) items1 = items as object[]; это не что иное, как попытка использовать ковариацию массивов, которая, как известно, работает только для ссылочных типов. Получается, для ссылочных типов используется класс SorterObjectArray, а для значимых типов используется SorterGenericArray. Но подождите, чем отличаются данные классы? Как вы можете заметить, они отличаются только способом доступа к элементам массива. Для значимых типов используются методы GetValue и SetValue, которые как вы знаете, являются очень медленными… Получается, что массив целых чисел будет сортироваться очень долго (ведь целое число является значимым типом)? Нет! Массив целых чисел сортируется быстро, причем очень быстро. Все дело в следующем коде
if (length > 1) { if (comparer == Comparer.Default || comparer == null) { if(TrySZSort(array, null, index, index + length - 1)) return; } } Интерес представляет метод Array.TrySZSort. Этот метод вызывает нативную реализацию сортировки реализованную на С++ в самой CLR. Причем работает он для примитивных типов, когда мы используем стандартную логику сравнения элементов, то есть когда comparer == Comparer.Default || comparer == null.
А вот и нативная реализация:
FCIMPL4(INT32, ArrayHelper::TrySZSort, ArrayBase * keys, ArrayBase * items, UINT32 left, UINT32 right) //если массив не является одномерным с начальным индексом ноль не сортируем if (keys->GetRank() != 1 || keys->GetLowerBoundsPtr()[0] != 0) return FALSE; // Получаем тип элементов массива TypeHandle keysTH = keys->GetElementTypeHandle(); // Если он не является встроенным примитивным const CorElementType keysElType = keysTH.GetSigCorElementType(); if (!CorTypeInfo::IsPrimitiveType(keysElType)) return FALSE; if (items != NULL) { TypeHandle itemsTH = items->GetElementTypeHandle(); if (keysTH != itemsTH) return FALSE; // Can't currently handle sorting different types of arrays. } // Оптимизация для массива из одного элемента if (left == right || right == 0xffffffff) return TRUE; //Далее вызывается специализированная версия сортировки написанная на шаблонах С++. switch(keysElType) { case ELEMENT_TYPE_I1: // 1-байтовое знаковое целое число (sbyte) ArrayHelpers<I1>::QuickSort((I1*) keys->GetDataPtr(), (I1*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_U1: // 1-байтовое целое число без знака (byte) case ELEMENT_TYPE_BOOLEAN: // Логический тип (bool) ArrayHelpers<U1>::QuickSort((U1*) keys->GetDataPtr(), (U1*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_I2: // 2-байтовое знаковое целое число (short) ArrayHelpers<I2>::QuickSort((I2*) keys->GetDataPtr(), (I2*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_U2: // 2-байтовое целое число без знака (ushort) case ELEMENT_TYPE_CHAR: // Символьный тип (char) ArrayHelpers<U2>::QuickSort((U2*) keys->GetDataPtr(), (U2*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_I4: // 4-байтовое знаковое целое число (int) ArrayHelpers<I4>::QuickSort((I4*) keys->GetDataPtr(), (I4*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_U4: // 4-байтовое целое число без знака (uint) ArrayHelpers<U4>::QuickSort((U4*) keys->GetDataPtr(), (U4*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_R4: // 4-байтовое число с плавающей запятой (float) ArrayHelpers<R4>::QuickSort((R4*) keys->GetDataPtr(), (R4*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_I8: // 8-байтовое знаковое целое число (long) ArrayHelpers<I8>::QuickSort((I8*) keys->GetDataPtr(), (I8*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_U8: // 8-байтовое целое число без знака (ulong) ArrayHelpers<U8>::QuickSort((U8*) keys->GetDataPtr(), (U8*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_R8: // 8-байтовое число с плавающей запятой (double) ArrayHelpers<R8>::QuickSort((R8*) keys->GetDataPtr(), (R8*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_I: // Размер целого числа в машинном коде (IntPtr) case ELEMENT_TYPE_U: // Размер целого числа без знака в машинном коде (UIntPtr) // In V1.0, IntPtr & UIntPtr are not fully supported types. They do // not implement IComparable, so searching & sorting for them should // fail. In V1.1 or V2.0, this should change. return FALSE; default: return FALSE; } return TRUE; }
// Шаблонный-класс непосредственно занимающийся сортировкой template <class KIND> class ArrayHelpers { static void QuickSort(KIND keys[], KIND items[], int left, int right) { do { int i = left; int j = right; KIND x = keys[(i + j) >> 1]; do { while (Compare(keys[i], x) < 0) i++; while (Compare(x, keys[j]) < 0) j--; if (i > j) break; if (i < j) { KIND key = keys[i]; keys[i] = keys[j]; keys[j] = key; if (items != NULL) { KIND item = items[i]; items[i] = items[j]; items[j] = item; } } i++; j--; } while (i <= j); if (j - left <= right - i) { if (left < j) QuickSort(keys, items, left, j); left = i; } else { if (i < right) QuickSort(keys, items, i, right); right = j; } } while (left < right); } };
Как видите, нативная сортировка работает только для примитивных типов. К ним относятся все числовые типы + логический + символьный. А для значимых пользовательских типов все будет работать плачевно медленно.
Переходим к рассмотрению реализации именно самого алгоритма сортировки. Будем рассматривать реализацию в классе SorterObjectArray, так как и нативная реализация и реализация для значимых типов аналогична.
1. В качестве опорного элемента всегда берется середина массива:
object obj1 = this.keys[left1 + right1 >> 1]; Это не хорошо, так как при плохих входных данных время выполнения алгоритма может стать квадратичным. К тому же середина берется по формуле num1 + num2 >> 1, что может привести к переполнению типа int. Такая же ошибка была сделана в алгоритме бинарного поиска и сортировки в Java (ссылка на баг).
Как увидите в следующих версиях .NET этот недостаток будет исправлен.
2. Для того, чтобы избежать переполнения стека в данной реализация предусмотрена оптимизация, устраняющая одну ветвь рекурсии: вместо того, чтобы после разделения массива вызывать рекурсивно процедуру разделения для обоих найденных подмассивов, рекурсивный вызов делается только для меньшего подмассива, а больший обрабатывается в цикле в пределах этого же вызова процедуры. С точки зрения эффективности в среднем случае разницы практически нет: накладные расходы на дополнительный рекурсивный вызов и на организацию сравнения длин подмассивов и цикла — примерно одного порядка. Зато глубина рекурсии, ни при каких обстоятельствах не превысит log2n, а в худшем случае вырожденного разделения она вообще будет не более 2 — вся обработка пройдёт в цикле первого уровня рекурсии.
.NET 2.0
Новая реализация претерпела незначительные изменения. Поскольку в .NET 2.0 появились обобщения, то я буду приводить обобщенный вариант сортировки.
public static void Sort<T>(T[] array, int index, int length, IComparer<T> comparer) { // TrySZSort все еще быстрее чем обобщенная реализация. // Причина заключается в том что вызов метода Int32.CompareTo выполняется медленнее чем "<" или ">". if (length <= 1 || (comparer == null || comparer == Comparer<T>.Default) && Array.TrySZSort((Array) array, (Array) null, index, index + length - 1)) return; ArraySortHelper<T>.Default.Sort(array, index, length, comparer); } А вот собственно метод, который сортирует
private static void SwapIfGreaterWithItems(T[] keys, IComparer<T> comparer, int a, int b) { if (a == b || comparer.Compare(keys[a], keys[b]) <= 0) return; T obj = keys[a]; keys[a] = keys[b]; keys[b] = obj; } internal static void QuickSort(T[] keys, int left, int right, IComparer<T> comparer) { do { int index1 = left; int index2 = right; int index3 = index1 + (index2 - index1 >> 1); ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index1, index3); ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index1, index2); ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index3, index2); T obj1 = keys[index3]; do { while (comparer.Compare(keys[index1], obj1) < 0) ++index1; while (comparer.Compare(obj1, keys[index2]) < 0) --index2; if (index1 <= index2) { if (index1 < index2) { T obj2 = keys[index1]; keys[index1] = keys[index2]; keys[index2] = obj2; } ++index1; --index2; } else break; } while (index1 <= index2); if (index2 - left <= right - index1) { if (left < index2) ArraySortHelper<T>.QuickSort(keys, left, index2, comparer); left = index1; } else { if (index1 < right) ArraySortHelper<T>.QuickSort(keys, index1, right, comparer); right = index2; } } while (left < right); }
Следует сказать, что оптимизация для встроенных примитивных типов все еще есть, не смотря на наличие обобщений (смотри комментарий разработчиков). То есть примитивные типы по-прежнему используют нативную сортировку.
В качестве опорного элемента теперь берется не середина массива, а медиана из первого, серединного и последнего элементов массива.
int index3 = index1 + (index2 - index1 >> 1); //середина ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index1, index3); ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index1, index2); ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index3, index2); T obj1 = keys[index3]; К тому же теперь середина вычисляется по формуле index1 + (index2 — index1 >> 1), что исключает ошибок связанных с переполнением.
В остальном все по-прежнему без изменений.
Теперь маленькое отступление: пусть нам надо отсортировать по убыванию массив целых чисел. Как вы будете это делать?
Учитывая все вышесказанное, следующий код
Array.Sort(a); Array.Reverse(a); на моем компьютере работает примерно в 3 раза быстрее, чем
Array.Sort(a, (x, y) => -x.CompareTo(y)) Вас может смутить тот факт, что метод Array.Reverse не обобщен, а значит, со значимыми типами будет работать медленно (упаковка и методы GetValue, SetValue), но если взглянуть на его реализацию мы опять увидим оптимизацию для встроенных значимых типов, а именно он вызывает нативный метод Array.TrySZReverse, который выглядит так:
template <class KIND> static void Reverse(KIND array[], UINT32 index, UINT32 count) { if (count == 0) { return; } UINT32 i = index; UINT32 j = index + count - 1; while(i < j) { KIND temp = array[i]; array[i] = array[j]; array[j] = temp; i++; j--; } } };
В общем оптимизации в стандартной библиотеке нас поджидают за каждым углом.
Кстати весьма странно, что нет обобщенной версии данного метода. Есть метод Reverse как метод расширение у Enumerable, но его недостаток в том, что он это делает не на месте. Получается, что вызов Array.Reverse на массиве пользовательских значимых типов всегда приводит к автобоксингу.
.NET 3.0 — .NET 4.0
Алгоритм не претерпел изменений.
.NET 4.5
Самое интересное начинается здесь!
Но прежде чем переходить к рассмотрению алгоритма, надо сказать пару слов о разворачивании .NET 4.5. Для полного понимания ситуации советую прочитать эту статью (к сожалению, на английском). При установке VS 2012, то есть при установки .NET 4.5 она заменяет сборки 4 фреймворка. Фактически это значит, что даже когда вы теперь пишете на .NET 4 вы использует сборки .NET 4.5. Получается интересная вещь: до установки 4.5 вы используете один алгоритм сортировки, после установки вы используете другой алгоритм, причем все происходит без вашего ведома.
Чтобы понять, что собственно происходит, взглянем на код из .NET 4.5:
public void Sort(T[] keys, int index, int length, IComparer<T> comparer) { if (BinaryCompatibility.TargetsAtLeast_Desktop_V4_5) ArraySortHelper<T>.IntrospectiveSort(keys, index, length, comparer); else ArraySortHelper<T>.DepthLimitedQuickSort(keys, index, length + index - 1, comparer, 32); } Как вы видите, в методе стоит проверка на то, в каком .NET мы работаем: если это 4.5, то мы используем IntrospectiveSort если это 4.0 то DepthLimitedQuickSort.
Давайте выясним чем отличается DepthLimitedQuickSort от сортировки, которая использовалась в .NET 4.0 до установки VS 2012. Взглянем на код этого метода:
internal static void DepthLimitedQuickSort(T[] keys, int left, int right, IComparer<T> comparer, int depthLimit) { while (depthLimit != 0) { int index1 = left; int index2 = right; int index3 = index1 + (index2 - index1 >> 1); ArraySortHelper<T>.SwapIfGreater(keys, comparer, index1, index3); ArraySortHelper<T>.SwapIfGreater(keys, comparer, index1, index2); ArraySortHelper<T>.SwapIfGreater(keys, comparer, index3, index2); T obj1 = keys[index3]; do { while (comparer.Compare(keys[index1], obj1) < 0) ++index1; while (comparer.Compare(obj1, keys[index2]) < 0) --index2; if (index1 <= index2) { if (index1 < index2) { T obj2 = keys[index1]; keys[index1] = keys[index2]; keys[index2] = obj2; } ++index1; --index2; } else break; } while (index1 <= index2); --depthLimit; if (index2 - left <= right - index1) { if (left < index2) ArraySortHelper<T>.DepthLimitedQuickSort(keys, left, index2, comparer, depthLimit); left = index1; } else { if (index1 < right) ArraySortHelper<T>.DepthLimitedQuickSort(keys, index1, right, comparer, depthLimit); right = index2; } if (left >= right) return; } ArraySortHelper<T>.Heapsort(keys, left, right, comparer); }
Как видите это та же быстрая сортировка за исключением одного: алгоритм переключается на пирамидальную сортировку, если мы исчерпаем глубину рекурсии, которая по умолчанию равна 32.
А вот собственно и пирамидальная сортировка:
private static void Heapsort(T[] keys, int lo, int hi, IComparer<T> comparer) { int n = hi - lo + 1; for (int i = n / 2; i >= 1; --i) ArraySortHelper<T>.DownHeap(keys, i, n, lo, comparer); for (int index = n; index > 1; --index) { ArraySortHelper<T>.Swap(keys, lo, lo + index - 1); ArraySortHelper<T>.DownHeap(keys, 1, index - 1, lo, comparer); } } private static void DownHeap(T[] keys, int i, int n, int lo, IComparer<T> comparer) { T x = keys[lo + i - 1]; for (; i <= n / 2; { int num; i = num;}) { num = 2 * i; if (num < n && comparer.Compare(keys[lo + num - 1], keys[lo + num]) < 0) ++num; if (comparer.Compare(x, keys[lo + num - 1]) < 0) keys[lo + i - 1] = keys[lo + num - 1]; else break; } keys[lo + i - 1] = x; }
Алгоритм DepthLimitedQuickSort есть ни что иное как IntroSort.
Introsort или интроспективная сортировка — алгоритм сортировки, предложенный Дэвидом Мюссером в 1997 году. Он использует быструю сортировку и переключается на пирамидальную сортировку, когда глубина рекурсии превысит некоторый заранее установленный уровень. Этот подход сочетает в себе достоинства обоих методов с худшим случаем O(n log n) и быстродействием, сравнимым с быстрой сортировкой. Так как оба алгоритма используют сравнения, этот алгоритм также принадлежит классу сортировок на основе сравнений.
Теперь посмотрим на то, что происходит в IntrospectiveSort. Фактически это та же интроспективная сортировка только более оптимизированная. Кстати, MSDN по-прежнему говорит, что использует быструю сортировку.
private static void IntroSort(T[] keys, int lo, int hi, int depthLimit, IComparer<T> comparer) { for (; hi > lo; {int num; hi = num - 1;}) { int num = hi - lo + 1; if (num <= 16) //если элементов меньше 16 используем сортировку вставками { if (num == 1) //если один элемент break; if (num == 2) //если два элемента { ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, hi); break; } else if (num == 3) //если три элемента { ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, hi - 1); ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, hi); ArraySortHelper<T>.SwapIfGreater(keys, comparer, hi - 1, hi); break; } else { ArraySortHelper<T>.InsertionSort(keys, lo, hi, comparer); //сортировка вставками break; } } else if (depthLimit == 0) //если исчерпали глубину рекурсии { ArraySortHelper<T>.Heapsort(keys, lo, hi, comparer); //используем пирамидальную сортировку break; } else // иначе используем разбиение быстрой сортировки { --depthLimit; num = ArraySortHelper<T>.PickPivotAndPartition(keys, lo, hi, comparer); ArraySortHelper<T>.IntroSort(keys, num + 1, hi, depthLimit, comparer); } } }
//разбиение массива алгоритмом быстрой сортировки private static int PickPivotAndPartition(T[] keys, int lo, int hi, IComparer<T> comparer) { int index = lo + (hi - lo) / 2; ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, index); ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, hi); ArraySortHelper<T>.SwapIfGreater(keys, comparer, index, hi); T obj = keys[index]; ArraySortHelper<T>.Swap(keys, index, hi - 1); int i = lo; int j = hi - 1; while (i < j) { do ; while (comparer.Compare(keys[++i], obj) < 0); do ; while (comparer.Compare(obj, keys[--j]) < 0); if (i < j) ArraySortHelper<T>.Swap(keys, i, j); else break; } ArraySortHelper<T>.Swap(keys, i, hi - 1); return i; }
//сортировка вставками private static void InsertionSort(T[] keys, int lo, int hi, IComparer<T> comparer) { for (int index1 = lo; index1 < hi; ++index1) { int index2 = index1; T x; for (x = keys[index1 + 1]; index2 >= lo && comparer.Compare(x, keys[index2]) < 0; --index2) keys[index2 + 1] = keys[index2]; keys[index2 + 1] = x; } }
Теперь сортировка в массивах представляет собой смесь сортировок: сортировку вставками, быструю сортировку и пирамидальную сортировку.
Использование Introsort положительно влияет на производительность, поскольку в реальных задачах данные бывают частично упорядочены, а на таких данных, как известно сортировка вставками работает очень быстро.
Сравнение производительности
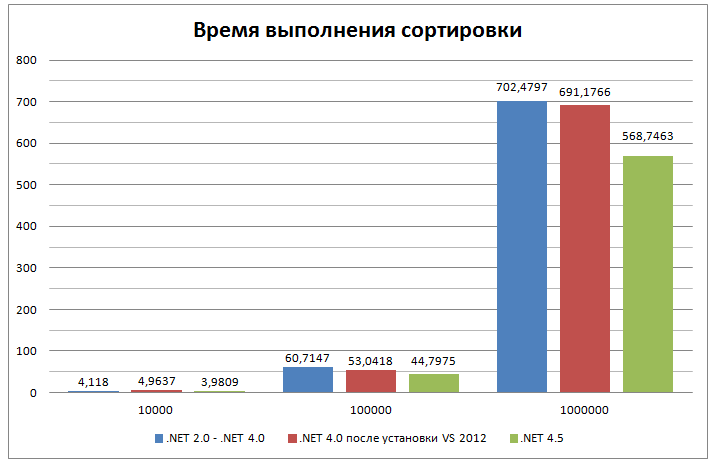
Сравнение с Java
В плане сортировки Java достаточно сильно отличается от .NET. Однако, как и в .NET в Java алгоритм так же менялся.
Как известно быстрая сортировка является неустойчивой, что является недостатком при сортировке ссылочных типов. Поскольку в Java «всё как бы объекты», то эта проблема усиливается, поэтому для сортировки ссылочных типов используется сортировка слиянием. Данная сортировка является устойчивой и гарантирует O(n logn) времени выполнения в худшем случае, однако и требует O(n) дополнительной памяти.
Поскольку проблема устойчивости касается только ссылочных типов, для примитивов не имеет значения, меняем ли мы элементы с одним ключом или нет. Поэтому для сортировки примитивов Java использует улучшенный алгоритм быстрой сортировки — DualPivotQuicksort. Обычный Quicksort делит массив на два отрезка, выбрав случайный элемент P. Потом сортирует массив так, чтобы все элементы меньше P попали в первый отрезок, а остальные — во второй. Затем алгоритм рекурсивно повторяется на первом и на втором отрезках. DualPivotQuicksort делит массив на три отрезка, вместо двух. В результате количество операций перемещения элементов массива существенно сокращается.
В Java 7 алгоритм сортировки ссылочных типов поменялся на TimSort.
Timsort — гибридный алгоритм сортировки, сочетающий сортировку вставками и сортировку слиянием, опубликованный в 2002 году Тимом Петерсом. В настоящее время Timsort является стандартным алгоритмом сортировки в Python, OpenJDK 7 и реализован в Android JDK 1.5. Основная идея алгоритма в том, что в реальном мире сортируемые массивы данных часто содержат в себе упорядоченные подмассивы. На таких данных Timsort существенно быстрее многих алгоритмов сортировки.
Timsort — быстр, однако на случайных данных уступает примерно на 30 процентов быстрой сортировке.
Что вы думаете об этом различии в реализации сортировки в двух фреймворках? Так ли нам нужна устойчивость в реальных задачах, на которую нужно потратить память, и время как это сделано в Java? Или же можно обойтись без устойчивости, взамен на скорость и экономию памяти как это сделано в .NET? Лично я отдаю свой выбор .NET, потому что думаю, что устойчивость нужна лишь в определенных задачах, которые возникают, не так часто, по крайней мере, у меня за 4 года не возникла ни раз, ну, а если и возникнет то решение таких проблем можно положить на плечи программиста, думаю, его не затруднит реализовать алгоритм устойчивой сортировки.
Заключение
Быть может такие подробности о .NET нужны не каждому программисту, но думаю, их знание не повредит никому. К тому же, изощренные интервьюеры могут задать вопросы о сортировке на собеседовании. В общем, спасибо за прочтение. Надеюсь, статья оказалась полезной.
ссылка на оригинал статьи http://habrahabr.ru/post/188012/
Добавить комментарий