В продолжение же моей предыдущей статьи описания скрытых моделей Маркова, задамся вопросом: откуда взять хорошую модель? Ответ достаточно стандартен, взять неплохую модель и сделать из нее хорошую.
Напомню пример: нам нужно реализовать детектор лжи, который по подрагиванию рук человека, определяет, говорит он правду или нет. Допустим, когда человек лжет, руки трясутся чуть больше, но нам не известно на сколько именно. Возьмем модель наобум, прогоним алгоритм Витерби из предыдущей статьи и получим довольно странные результаты:
Никакого смысла в получившемся разбиении нет; точнее, есть, но не то который хотелось бы видеть. Первый вопрос: как оценить вероятность появления имеющейся выборки в выбранной модели. И второй вопрос, как найти такую модель, в которой имеющаяся выборка была бы наиболее правдоподобна, то есть как оценить качество и как организовать адаптивность к новым данным. Как раз на них и отвечают the forward-backward procedure и the Baum-Welch reestimation procedure.
The forward-backward procedure позволяет оценить вероятность того, что в данной модели HMM появится выборка наблюдаемых значений  (Обозначения взяты из предыдущей статьи). Обозначим оценочную функцию как
(Обозначения взяты из предыдущей статьи). Обозначим оценочную функцию как  . И введем две дополнительные функции:
. И введем две дополнительные функции:
AlphaFunc<-function(S,I,T,P,O,Tm) { la<-I*Es(P,O[1]) alpha<-cbind(la) for(t in 2:Tm) { la<-as.vector((la*Es(P,O[t]))%*%T) alpha<-cbind(alpha,la) } return (alpha) } BetaFunc<-function(S,I,T,P,O,Tm) { lb<-rep(1,length(S)) beta<-cbind(lb) for(t in Tm:2) { lb<-as.vector(T%*%(Es(P,O[t])*lb)) beta<-cbind(lb, beta) } return (beta) } Функции  ,
,  обладают следующими интересными свойствами:
обладают следующими интересными свойствами:

Итак, мы уже умеем оценивать появление выборки O в модели HMM и находить последовательность скрытых состояний  . Открытым остается вопрос, как найти модель, в которой вероятность появления имеющейся выборки будет максимальной, то есть
. Открытым остается вопрос, как найти модель, в которой вероятность появления имеющейся выборки будет максимальной, то есть  , где
, где  некоторое множество допустимых моделей. Как утверждается, формального алгоритма нахождения оптимума нет, но зачастую можно хотя бы на капельку приблизиться к «совершенству», за счёт некоторой модификации модели. Именно так и работают итерационные EM-алгоритмы.
некоторое множество допустимых моделей. Как утверждается, формального алгоритма нахождения оптимума нет, но зачастую можно хотя бы на капельку приблизиться к «совершенству», за счёт некоторой модификации модели. Именно так и работают итерационные EM-алгоритмы.
Итак, пусть есть начальная модель  необходимо найти такую модель
необходимо найти такую модель  , что
, что  . Приступим.
. Приступим.
Введем еще две вспомогательные функции:
xiGamma<-function(t,alpha,beta,S,T,P,O) { xi<-matrix(0,nrow=length(S),ncol=length(S)) denom<-alpha[,t]%*%beta[,t] for(sin in S) { for(sout in S) { nom<-alpha[sin,t]*T[sin,sout]*Es(P,O[t+1])[sout]*beta[sout,t+1] xi[sin,sout]<-nom/denom } } return(list(xi=xi,g=rowSums(xi))) } XiGammas<-function(Tm,alpha,beta,S,T,P,O) { xis<-c() gs<-c() for(t in 1:(Tm-1)) { xg<-xiGamma(t,alpha,beta,S,T,P,O) xis<-cbind(xis,as.vector(xg$xi)) gs<-cbind(gs,as.vector(xg$g)) } return(list(xi=xis,g=gs)) }  интерпретируется как доля переходов из состояния s в состояние s’ в момент времени t, а
интерпретируется как доля переходов из состояния s в состояние s’ в момент времени t, а  – как общая доля переходов из состояния s в момент времени t.
– как общая доля переходов из состояния s в момент времени t.
Подправленные параметры модели  будут иметь следующий вид:
будут иметь следующий вид:
BaumWelshFunc<-function(S,I,T,P,O,Tm) { a<-alphaLog(S,I,T,P,O,Tm) b<-betaLog(S,I,T,P,O,Tm) xg<-XiGammas(Tm, a,b, S,T,P,O) xi<-rowSums(xg$xi) dim(xi)<-c(length(S),length(S)) g<-rowSums(xi) new_I <- g/sum(g) small_t<-rep(g,length(S)) dim(small_t)<-c(length(S),length(S)) new_T <- xi/small_t norm_params<-NormalReestimation(xg$g,O[1:(Tm-1)],S) new_P<-c() for(s in S) { new_P<-c(new_P,Curry("dnorm",mean=norm_params$mu[s], sd=sqrt(norm_params$sigma2[s]))) } return(list(S=S,I=new_I,T=new_T,P=new_P,N=norm_params)) } Перенастройка функции  (NormalReestimation в нашем случае) зависит от конкретной ситуации. Классическая реализация алгоритма предполагает, что наблюдения описываются конечными дискретными распределениями, что нам не подходит. Предлагается использовать следующий метод оценки параметров для наблюдаемых величин:
(NormalReestimation в нашем случае) зависит от конкретной ситуации. Классическая реализация алгоритма предполагает, что наблюдения описываются конечными дискретными распределениями, что нам не подходит. Предлагается использовать следующий метод оценки параметров для наблюдаемых величин:
NormalReestimation<-function(g,O,S) { denom<-rowSums(g) mu<-g%*%O/denom sigma2<-c() for(s in S) { s2<-g[s,]%*%(O-mu[s])^2 sigma2<-c(sigma2,s2) } return(list(mu=as.vector(mu),sigma2=sigma2/denom)) } Рассмотрим задачу о детекторе лжи в более общем варианте. У нас есть общая модель того, как наш детектор лжи реагирует на ложь и искренность субъектов и есть конкретный индивид, который иногда врет иногда говорит правду. Мы хотим настроить нашу модель на работу с этим, конкретным индивидом.
Дано:
- Модель. Имеются два скрытых состояния, когда сферический человек говорит правду и когда лжет. В том и в другом случае подёргивание рук можно представить как белый шум, но диспер
- Выборка из 10000 последовательных наблюдений за нашим индивидом.
Необходимо:
- Оценить дисперсию подрагивания рук в случае искренности/лжи этого индивида.
- Определить моменты смены этих состояний для него.
Решение:
- Зададим нашу пятерку:
- Число состояний
 ;
; - Состояния
 ;
; - Начальное распределение
 ;
; - По умолчанию предположим, что состояния равноправны и скажем смена происходит в среднем, раз в 999 тактов времени:
 ;
;  , где
, где  .
.
Поясню, что – это выборочная дисперсия для всей выборки целиком. Начальные оценочные функции для
– это выборочная дисперсия для всей выборки целиком. Начальные оценочные функции для  выбираются таким образом, чтобы первое состояние отвечало меньшим значениям дисперсии, а второе – большим. Существенно, что они разные.
выбираются таким образом, чтобы первое состояние отвечало меньшим значениям дисперсии, а второе – большим. Существенно, что они разные.
- Число состояний
- Будем перенастраивать параметры с помощью алгоритма Баума-Велша до тех пор, пока значение оценочной функции не стабилизируется.
- Найдем наиболее правдоподобные скрытые состояния для каждого момента времени с помощью алгоритма Витерби.
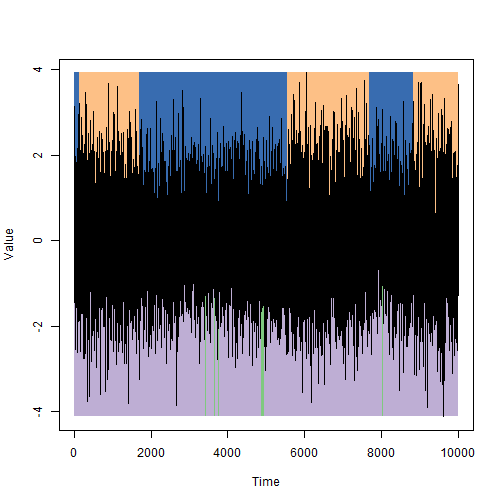
Ответ проиллюстрируем на данных с первой картинки: сверху состояния, как они были заданы при моделировании, снизу состояния, которые были выделены с помощью метода скрытых цепей Маркова.

На графике ниже приведем значения логарифма оценочной функции в зависимости от числа итераций алгоритма Баума-Велша. Зеленым цветом отмечена оценка, соответствующая параметрам моделирования.

Ошибка в оценке скрытых состояний относительно маленькая, но только когда начальное приближение не сильно отличается от того, что мы хотим найти. Нужно понимать, что алгоритм Баума-Велша всего лишь шаг поиска локального оптимума, а значит, может никогда не достигнуть глобального экстремума.
Формулы превращены в картинки с помощью mathurl.com. Надеюсь, когда-нибудь, здесь можно будет вставлять формулы более простым и приятным глазу способом и, кстати, очень не хватает подсветки синтаксиса для R.
ссылка на оригинал статьи http://habrahabr.ru/post/188244/
Добавить комментарий