Решение задачи кластеризации методом градиентного спуска

Данные

В первую очередь давайте обсудим множество данных, на котором мы будем тестировать алгоритмы. Для тестирования используется множество данных с датчиков смартфонов: всего 563 поля в 7352 наблюдений; из низ 2 поля выделены для идентификатора пользователя и типа действия. Множество создано для классификации действия пользователя в зависимости от показаний датчиков, всего 6 действий (WALKING, WALKING_UPSTAIRS, WALKING_DOWNSTAIRS, SITTING, STANDING, LAYING). Более подробное описание множества вы можете найти по вышеприведенной ссылке.

Как вы понимаете визуализировать такое множество, не уменьшая размерности, немного проблематично. Для уменьшения размерности использовался метод главных компонент, для этого можно использовать стандартные средства языка R, либо реализацию этого метода на том же языке из моего репозитория. Давайте взглянем на то как выглядит исходное множество, спроецированное на первый и третий главный компонент.

m.proj <- ProjectData(m.raw, e$eigenVectors[, c(1, 3)]) plot(m.proj[, 1], m.proj[, 2], pch=19,       col=rainbow(6)[unclass(as.factor(samsungData$activity))],       xlab="first", ylab="third",       main="Two components; actions") 

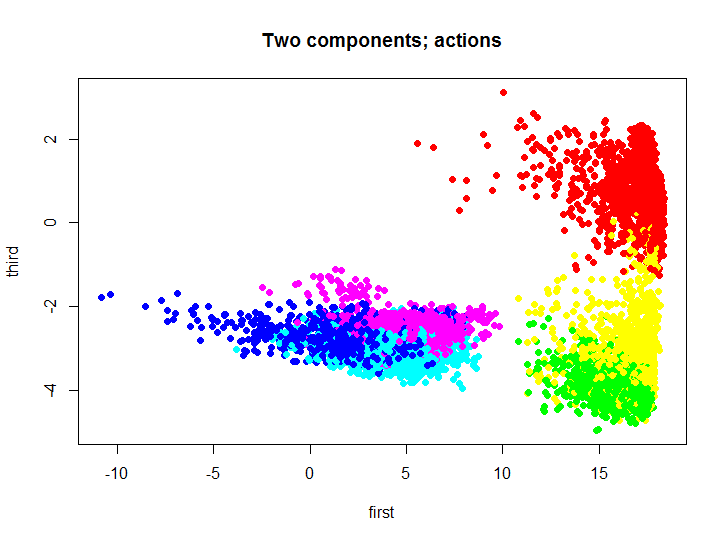
Различными цветами обозначены различные действия, далее мы будем использовать это двухмерное множество для тестирования и визуализации результатов работы кластеризации.

Функция стоимости алгоритма k-means

Введем следующие обозначения:

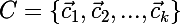• — множество центроидов 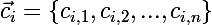соответствующих кластеров
• — исходное множество данных, которое необходимо кластеризировать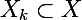
• — k-ый кластер, подмножество исходного множества

А теперь рассмотрим функцию стоимости классического алгоритма k-means:

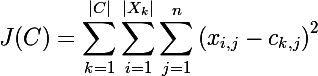
т.е. алгоритм минимизирует суммарное квадратичное отклонение элементов кластера от центроида. Другими словами, минимизируется сумма квадратов Евклидова расстояния элементов кластера от соответствующего центроида:
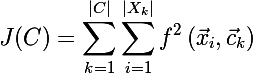, где f — в данном случае является Евклидовым расстоянием.

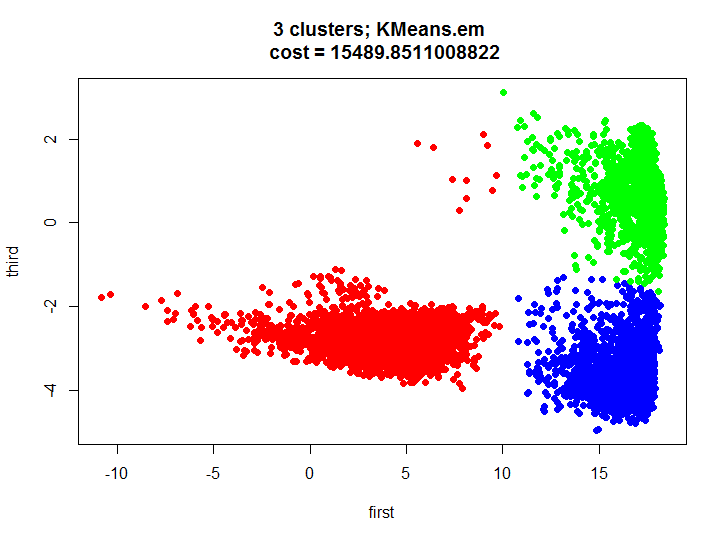
Как известно для решения этой проблемы существует эффективный алгоритм обучения основанный на алгоритме expectation-maximization. Давайте взглянем на результат работы этого алгоритма, используя встроенную в R функцию:

kmeans.inner <- kmeans(m.proj, 3) plot(m.proj[, 1], m.proj[, 2], pch=19,       col=rainbow(3)[unclass(as.factor(kmeans.inner$cluster))],      xlab="first", ylab="third",       main=paste(k, " clusters; kmeans \n cost = ", kmeans.inner$tot.withinss/2, sep="")) 

Градиентный спуск

Сам алгоритм градиентного спуска довольно таки прост, суть в том что бы двигаться небольшими шажками в сторону обратную направлению градиента, так например работает алгоритм обратного распространения ошибки, или алгоритм contrastive divergence для обучения ограниченной машины Больцмана. Перво-наперво необходимо рассчитать градиент целевой функции, или же частные производные целевой функции по параметрам модели.

, раз уж мы вышли из секции про классический k-means, то и f может быть в принципе любой мерой расстояния, не обязательно Евклидовой метрикой

Но тут есть проблема, мы не знаем на данном этапе каково разбиение множества X на кластеры. Давайте попробуем переформулировать целевую функцию так, что бы записать ее в виде одной формулы, что бы легко было продифференцировать: сумма минимальных расстояний от каждого элемента множества до одного из трех центроидов. Эта формула выглядит следующим образом:

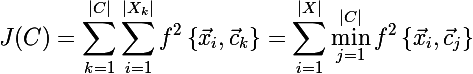
Теперь давайте найдем производную новой целевой функции:

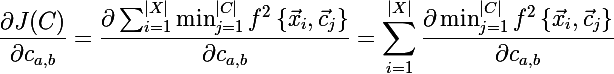
Ну что ж, осталось выяснить чему равна производная минимума, но тут оказывается все просто: в случае если a-ый центройд это действительно тот, до которого расстояние минимально от текущего элемента множества, то производная выражения равна производной квадрата расстояния по элементу вектора, в противном случае равна нулю:

Реализация метода

Как вы понимаете все шаги из предыдущего пункта можно выполнить, не возводя расстояние в квадрат. Так и было сделано при реализации этого метода. Метод получает в качестве параметров функцию расстояния и функцию вычисления частной производной функции расстояния между двумя векторами по компоненту второго вектора, приведу для примера «половину квадрата Евклидова расстояния» (удобно использовать т.к. производная очень проста), а так же саму функцию градиентного спуска:

HalfSqEuclidian.distance <- function(u, v) {   # Half of Squeared of Euclidian distance between two vectors   #   # Args:   #   u: first vector   #   v: second vector   #   # Returns:   #   value of distance   return(sum((u-v)*(u-v))/2)    } 

HalfSqEuclidian.derivative <- function(u, v, i) {   # Partial derivative of Half of Squeared of Euclidian distance    # between two vectors   #   # Args:   #   u: first vector   #   v: second vector   #   i: index of part of second vector   #   # Returns:   #   value of derivative of the distance   return(v[i] - u[i]) } 

 KMeans.gd <- function(k, data, distance, derivative,                       accuracy = 0.1, maxIterations = 1000,                        learningRate = 1,                        initialCentroids = NULL, showLog = F) {   # Gradient descent version of kmeans clustering algorithm   #   # Args:   #   k: number of clusters   #   data: data frame or matrix (rows are observations)   #   distance: cost function / metrics   #   centroid: centroid function of data   #   accuracy: accuracy of calculation   #   learningRate: learning rate   #   initialCentroids: initizalization of centroids   #   showLog: show log      n <- dim(data)[2]   c <- initialCentroids      InitNewCentroid <- function(m)   {     c <- data[sample(1:dim(data)[1], m), ]   }      if(is.null(initialCentroids))   {     c <- InitNewCentroid(k)   }      costVec <- vector()   cost <- NA   d <- NA   lastCost <- Inf   for(iter in 1:maxIterations)   {     g <- matrix(rep(NA, n*k), nrow=k, ncol=n)          #calculate distances between centroids and data     d <- matrix(rep(NA, k*dim(data)[1]), nrow=k, ncol=dim(data)[1])     for(i in 1:k)     {       d[i, ] <- apply(data, 1, FUN = function(v) {distance(v, c[i, ])})     }          #calculate cost     cost <- 0     for(i in 1:dim(data)[1])     {       cost <- cost + min(d[, i])     }     if(showLog)     {       print(paste("Iter: ", iter,"; Cost = ", cost, sep=""))     }     costVec <- append(costVec, cost)          #stop conditions     if(abs(lastCost - cost) < accuracy)     {       break     }     lastCost <- cost          #calculate gradients     for(a in 1:k)     {       for(b in 1:n)       {         g[a, b] <- 0         for(i in 1:dim(data)[1])         {           if(min(d[, i]) == d[a, i])           {             g[a, b] <- g[a, b] + derivative(data[i, ], c[a, ], b)           }         }                }     }          #update centroids     for(a in 1:k)     {       for(b in 1:n)       {         c[a, b] <- c[a, b] - learningRate*g[a, b]/dim(data)[1]       }     }   }      labels <- rep(NA, dim(data)[1])   for(i in 1:dim(data)[1])   {     labels[i] <- which(d[, i] == min(d[, i]))   }   return(list(     labels = labels,     cost = costVec   )) } 

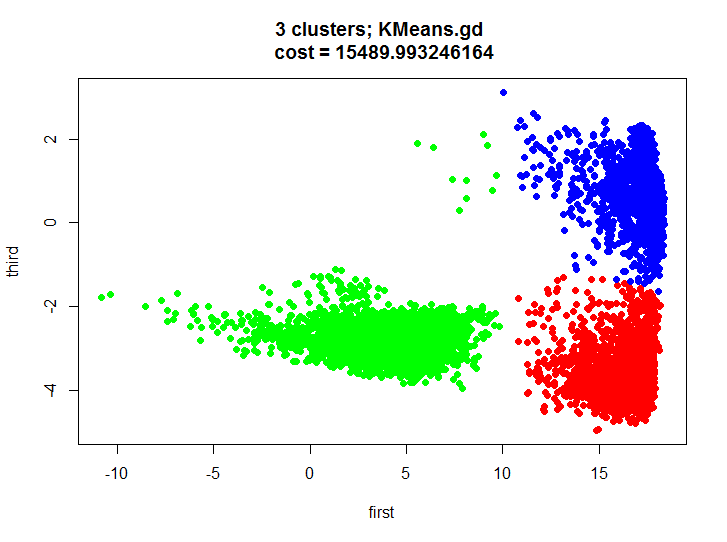
KMeans.gd.result <- KMeans.gd(k, m.proj, HalfSqEuclidian.distance,                                HalfSqEuclidian.derivative, showLog = T) plot(m.proj[, 1], m.proj[, 2], pch=19,       col=rainbow(k)[unclass(as.factor(KMeans.gd.result$labels))],      xlab="first", ylab="third",       main=paste(k, " clusters; KMeans.gd \n cost = ", KMeans.gd.result$cost[length(KMeans.gd.result$cost)], sep="")) 

Давайте взглянем на результат кластеризации и убедимся что он почти идентичен.

А так выглядит динамика значения функции стоимости от итерации у обоих алгоритмов:

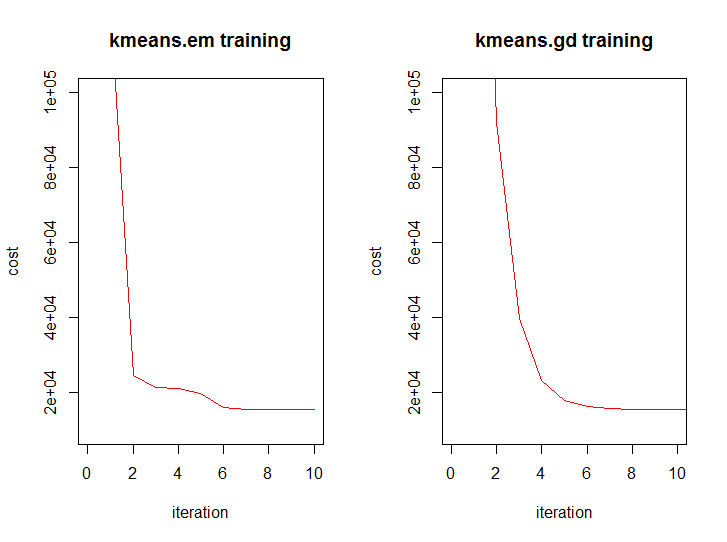
Заключение

Давайте скажем сначала пару слов о том, что же получилось в нашем тесте. Мы получили приличное разбиение двухмерного множества на три кластера, мы визуально видим что кластеры не сильно пересекаются и можно вполне строить модели для распознавания действия для каждого кластера, тем самым получится некоторая гибридная модель (один кластер содержит в основном одно действие, другой два, а третий три).

Взглянем на сложности алгоритмов при кластеризации используя Евклидово расстояние, рассмотрим только одну итерацию (анализ же количества итераций является совсем не тривиальной задачей). Обозначим за k — количество кластеров, n — размерность данных, m — количество данных (k <= m). В экстремальном случае k = m.

• EM версия:
• GD версия:

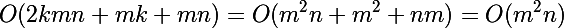
В общем математически то оба алгоритма стоят на одной ступени, но мы то знаем что один чуть выше -)

Весь код вы можете найти здесь.