Привет, %username%!
Недавно на хабре была опубликована очень спорная статья под названием «Эксперты призывают готовиться к криптоапокалипсису». Честно говоря, я не согласен с выводами авторов о том, что «голактеко опасносте», все скоро взломают и подорожает гречка. Однако я хочу поговорить не об этом.
В комментариях к той статье я высказал мнение, что кое в чем докладчики правы и переходить на эллиптическую криптографию уже давно пора. Ну в самом деле, кто-нибудь видел в интернете ECDSA сертификат? Хотя стандарту уже без малого 13 лет, мы продолжаем по старинке использовать старый добрый RSA. В общем сказал я это, и как это часто бывает, задумался а так ли необходим переход на «эллиптику»? Да и что это за зверь такой эллиптическая криптография? Какие имеет плюсы, минусы, тонкости. Одним словом, давайте разбираться.
Эллиптические кривые
Эллиптическая кривая — это набор точек, описывающихся уравнением Вейерштрассе:
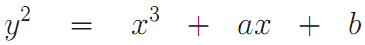
Типичные варианты графиков эллиптических кривых вы сможете посмотреть под спойлером:
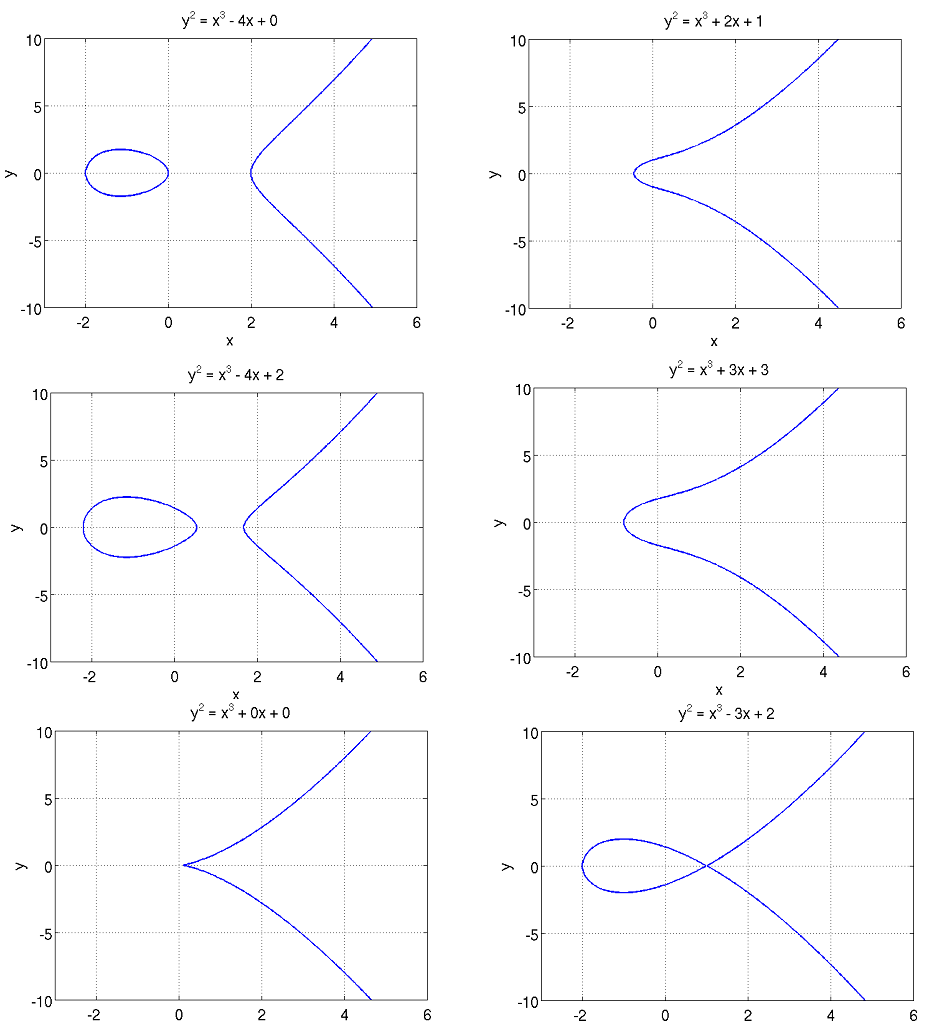
Эллиптические кривые представленые на первых 4-х рисунках называются гладкими. В то время как две нижние кривые относятся к т.н. сингулярным эллиптическим кривым.
Для гладких эллиптических кривых выполняется следующее неравенство:

Тогда как для сингулярных кривых это условие, сюрприз, не выполняется.
Если вы собираетесь самостоятельно разрабатывать криптографических продукт, поддерживающий «эллиптику» очень важно запомнить следующий факт:
Нельзя использовать в схемах ЭЦП сингулярные кривые. Подробно мы еще затронем эту тему, сейчас же просто скажем, что используя сингулярные кривые вы рискуете значительно снизить стойкость схемы ЭЦП.
Арифметические операции в эллиптической криптографии производятся над точками кривой. Основной операцией является «сложение».
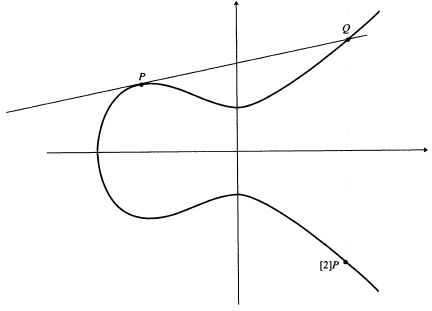
Сложение двух точек легко представить графически:

Как видно из рисунка, для сложения точек P и Q, необходимо провести между ними прямую линию, которая обязательно пересечет прямую в какой-либо третьей точке R. Отразим точку R относительно горизонтальной оси координат и получим искомую точку P+Q.
Алгебраическое представление «сложения»
Запишем сложение двух точек в виде формулы:

Пусть координатами точки P будут (xp, yp), а координатами точки Q соответственно (xq, yq). Вычислим

и тогда координаты точки P+Q будут равны:
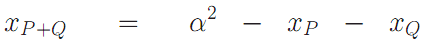
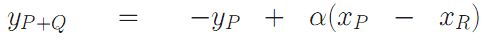
Эллиптические кривые в криптографии
Осталось уточнить всего одну деталь. Все рассмотренные выше кривые относятся к эллиптическим кривым над вещественными числами. И это приводит нас к проблеме округления. Т.е., используя кривые над вещественными числами, мы не сможем получить биекцию между исходным текстом и зашифрованными данными. Чтобы не заморачиваться с округлением в криптографии используются только кривые над конечными полями. Это означает, что под эллиптической кривой понимается набор точек, чьи координаты принадлежат конечному полю.
В криптографии рассматривается два вида эллиптических кривых: над конечным полем  — кольцо вычетов по модулю простого числа. И над полем
— кольцо вычетов по модулю простого числа. И над полем  — бинарное конечное поле.
— бинарное конечное поле.
У эллиптических кривых над полем  есть одно важное преимущество, элементы поля
есть одно важное преимущество, элементы поля  могут быть легко представленны в виде n-битных кодовых слов, это позволяет увеличить скорость аппаратной реализации эллиптических алгоритмов.
могут быть легко представленны в виде n-битных кодовых слов, это позволяет увеличить скорость аппаратной реализации эллиптических алгоритмов.
Однако здесь есть свои подводные камни. Если мы сложим два одинаковых элемента из бинарного конечного поля, то получим в результате 0, т.к. сложение происходит по модулю 2. Это означает что характеристика такого поля равна 2. Но эллиптическая кривая вида
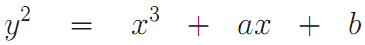
описанная над полем характеристики 2 или 3 становится сингулярной, а как уже замечалось выше это неудачная идея использовать сингулярные кривые в криптографии.
Поэтому над бинарным конечным полем используются кривые вида:

Еще одним важным понятие эллиптической криптографии является порядок эллиптической кривой, который показывает количество точек кривой над конечным полем.
Теорема Хассе утверждает, что если N — количество точек кривой, определенной над полем Zq с q элементами тогда справедливо равенство:

Т.к. бинарное конечное поле 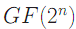 состоит из 2n элементов мы можем сказать, что порядок кривой
состоит из 2n элементов мы можем сказать, что порядок кривой  равен
равен  , где
, где 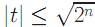 .
.
С числом t связано следующее определение:
эллиптическая кривая над бинарным конечным полем называется суперсингулярной, если t делится на 2 без остатка.
Разумеется все это я к тому, что нельзя использовать в схемах ЭЦП суперсингулярные кривые. Строгая рекомендация не использовать сингулярные и суперсингулярные кривые для цифровой подписи имеет одну очень вескую причину, но об этом позже.
Криптография на эллиптических кривых
Точки эллиптической кривой над конечным полем представляют собой группу. И как мы отмечали выше для этой группы определена операция сложения.
Соответственно мы можем представить умножение числа k на точку G как G+G+..+G с k слагаемыми.
Теперь представим, что у нас имеется сообщение M представленное в виде целого числа. Мы можем зашифровать его используя выражение
C-M*G.
Вопрос в том, насколько сложно восстановить M зная параметры кривой E(a,b), шифротекст С и точку G.
Данная задача называется дискретным логарифмом на эллиптической кривой и не имеет быстрого решения. Более того, считается, что задача дискретного логарифма на эллиптической кривой является более трудной для решения, чем задача дискретного логарифмирования в конечных полях.
Наиболее быстрые методы, разработанные для конечных полей оказываются бесполезны в случае эллиптических кривых.
Так для решения дискретного логарифма существуют достаточно быстрые алгоритмы имеющие сложность  , где c и d — некоторые константы, а p — размер поля. Такие алгоритмы называются субэкспоненциальными и позволяют сравнительно легко вскрывать дискретный логарифм в конечном поле, если размер поля не выбран очень большим, порядка 21024.
, где c и d — некоторые константы, а p — размер поля. Такие алгоритмы называются субэкспоненциальными и позволяют сравнительно легко вскрывать дискретный логарифм в конечном поле, если размер поля не выбран очень большим, порядка 21024.
В тоже время наиболее быстрые методы решения дискретного логарифма на эллиптической кривой имеют сложность 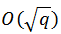 , где q — количество точек эллиптической кривой.
, где q — количество точек эллиптической кривой.
Таким образом, для обеспечения уровня стойкости в 280 операций необходимо чтобы q=2160. Напомню, для того, чтобы получить аналогичный уровень сложности при вычислении дискретного логарифма в конечном поле необходимо поле порядка q=21024.
Следует, однако, заметить, что поскольку мощность вычислительной техники постоянно повышается, значение q будет постоянно увеличиваться. Но так как графики функций 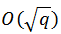 и
и  резко отличаются друг от друга, в группе точек эллиптической кривой q будет расти намного медленнее, чем в произвольном конечном поле.
резко отличаются друг от друга, в группе точек эллиптической кривой q будет расти намного медленнее, чем в произвольном конечном поле.
Варианты атак
- Алгоритма Полига-Хеллмана. Алгоритм решения дискретного логарифма. Предположим, что n — количество точек эллиптической кривой. Пусть число n раскладывается на простые числа p1, p2,.., pn. Суть метода сводится к тому, чтобы найти дискретные логарифмы по модулю числе pi, а затем получить общее решение с помощью китайской теореме об остатках. Атака позволяет свести проблему дискретного логарифма в большом поле n к той же задаче, но с гораздо меньшим полем p. Для того, чтобы противостоять атака необходимо просто выбирать кривые, количество точек которых делится на очень большое простое число q≈n.
- Алгоритм Шенкса, более известный как шаги младенца/шаги гиганта. Типичный пример time memory trade off. Для группы размером n вычисляется таблиц размером n1/2, затем по этой таблице происходит поиск нужного элемента. Сложность алгоритма
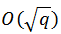 .
. - Уязвимость сингулярных и суперсингулярных кривых. Я уже упоминал, что для решения задачи дискретного логарифма не существует субэкспоненциальных методов решения. На самом деле есть одна оговорка, такие методы есть, но только для определенного рода кривых: сингулярных и суперсингулярных. Особые свойства таких кривых позволяют свести задачу дискретного логарифма на эллиптической кривой, к задаче дискретного логарифма в конечном поле. Соответственно для такого класса кривых стандартные ключи размером в 160-320 бит, будут фатально уязвимы, что позволит злоумышленникам вскрыть секретный ключ, за относительно небольшое время.
- Уязвимость аномальных кривых Напомню, что количество точек эллиптической кривой вычисляется по формуле
 . И что кривая называется суперсингулярной если t делится на 2.
. И что кривая называется суперсингулярной если t делится на 2.
Поэтому, на первый взгляд может показаться хорошей идеей использовать кривые в которых количество точек равно 2n, т.е. n=1.
Однако такие кривые называются аномальными и решение дискретного логарифма на аномальных эллиптических кривых является еще более простой задачей, чем для суперсингулярных и сингулярных кривых.
Подытожим
На основании всего вышесказанного выпишем основные достоинства и недостатки эллиптической криптографии:
Итак, основные плюсы:
- Гораздо меньшая длина ключа по сравнению к «классической» асимметричной криптографией.
- Скорость работы эллиптических алгоритмов гораздо выше, чем у классических. Это объясняется как размерами поля, так и применением более близкой для компьютеров структуры бинарного конечного поля.
- Из-за маленькой длины ключа и высокой скорости работы, алгоритмы асимметричной криптографии на эллиптических кривых могут использоваться в смарт-картах и других устройствах с ограниченными вычислительными ресурсами.
Основные минусы эллиптической криптографии:
- Все плюсы эллиптической криптографии вытекают из одного конкретного факта:
для задачи дискретного логарифмирования на эллиптических кривых не существует субэкспоненциальных алгоритмов решения. Это позволяет уменьшить длину ключа и увеличить производительность. Однако если такие алгоритмы появятся, то это будет означать крах эллиптической криптографии. - Эллиптическая криптография — это очень сложно. Не то чтобы я считал обычную асимметричную криптографию совсем уж простой штукой. Но «эллиптика» — это огромное количество тонкостей, которые необходимо учесть. Начиная с выбора эллиптической кривой и заканчивая генерацией ключей. При массовом переходе на эллиптику скорее всего обязательно будет большое количество ошибок и уязвимостей, которые уже отработаны для более привычных методов.
На основании всего вышесказанного, я сделал для себя вывод, что повсеместный переход на «эллиптику» не является необходимостью. В конце концов, пока мирно сосуществуют обычные RSA, DSA с одной стороны, и ГОСТ 34.10, ECDSA с другой, есть пусть и ложное, но успокаивающее чувство альтернативы, которого мы можем лишиться, погнавшись за самыми современными криптографическими методами.
Используемая литература
- Don Johnson, Alfred Menezes, Scott Vanstone — The Elliptic Curve Digital Signature Algorithm.
- А. Болотов, С. Гашков, А. Фролов, А. Часовских — Элементарное введение в эллиптическую криптографию.
- Lawrence Washington — Elliptic curves, Number theory and Cryptography.
ссылка на оригинал статьи http://habrahabr.ru/post/188958/
Добавить комментарий