Предположим, вы хотите создать игру.

data Point = Point { _x, _y   :: Double } data Mario = Mario { _location :: Point }  player1 = Mario (Point 0 0) 

Отлично, хотели бы вы теперь перемещать персонажа?

moveX (Mario (Point xpos ypos)) val = Mario (Point (xpos + val) ypos) 

Взамен, lenses (линзы) позволяют вам написать что-то такое:

location.x `over` (+10) $ player1 

Или вот так:

over (location . x) (+10) player1 

Линзы позволяют тебе выборочно изменять часть ваших данных.

Намного понятнее! Полный пример здесь

{-# LANGUAGE TemplateHaskell #-}   import Control.Lens   data Point = Point {            _x :: Double,            _y :: Double            } deriving (Show)   data Mario = Mario { _location :: Point } deriving (Show)   makeLenses ''Point makeLenses ''Mario   player1 = Mario (Point 0 0)   main = print (location.x +~ 10 $ player1) 

location — линза, x тоже линза. Здесь я комбинирую эти линзы, чтобы изменять части player1.

Fmap

Вы наверное знаете как работает fmap. Доктор Ватсон ( прочитайте это если нет):

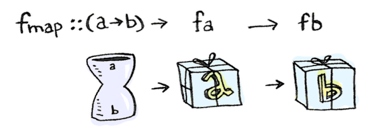
Отлично, дружище, что если взамен у тебя вложенные функторы?

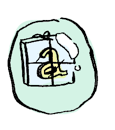
Ты должен использовать два fmap !

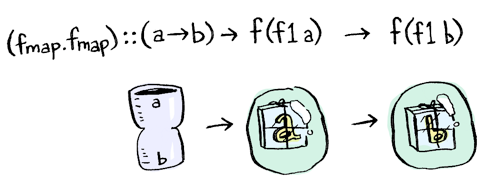
Теперь, ты уже наверное знаешь как работает композиция функций:

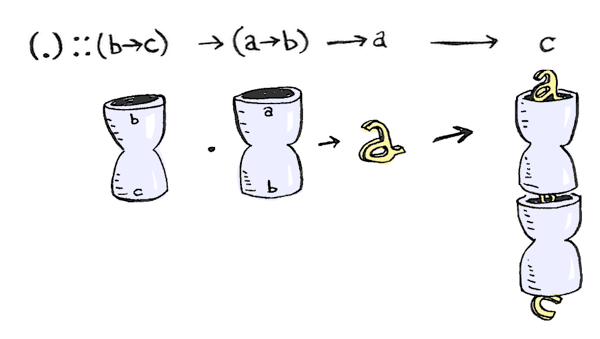
Как насчет композиции композиции функций?

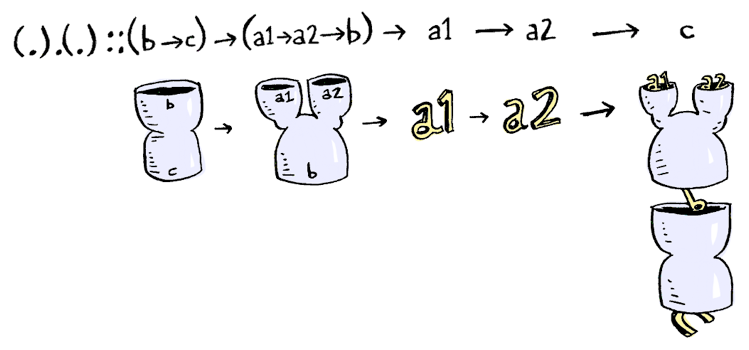
«Если ты хочешь использовать композицию функций, где фунция имеет два аргумента», говорит Шерлок, «тебе нужно (.).(.)!”»
«Это похоже на испуганную сову», восклицает Ватсон
«Действительно. Давай разберемся как это работает»

Сигнатура типа для композиции функций выглядит так:

(.) :: (b -> c) -> (a -> b) -> (a -> c) 

Что чертовски похоже на fmap !

fmap :: (a -> b) -> f a -> f b 

На самом деле если ты заменишь a-> на f это будет точно fmap!
И знаешь что! a-> функтор! Который определяется вот так:

instance Functor ((->) r) where    fmap = (.) 

Таким образом, fmap является композицией функций! (.).(.) тоже самое что и fmap.fmap!

(.).(.) :: (b -> c) -> (a1 -> a2 -> b) -> (a1 -> a2 -> c) fmap . fmap :: (a -> b) -> f (f1 a) -> f (f1 b) 

Здесь есть повторяющийся шаблон: и fmap . fmap и (.).(.) позволяют нам «уйти на уровень глубже». В fmap это означает уйти на 1 уровень функторов вглубь. При композиции функций твой функтор это r->, это значит что ты можешь передать еще один аргумент своей функции.

Сеттеры(Setters)

Предположим у тебя есть функция double типа такой:

double :: Int -> Maybe Int double x = Just (x * 2)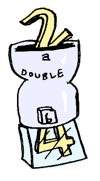 

Ты можешь применить ее к списку с помощью traverse:

Получается ты передаешь обходимое и функцию, которая возвращает значение обернутое в функтор. Ты получаешь обратно обходимое обернутое в функтор. Как обычно, ты можешь пойти на один уровень глубже составляя traverse:

traverse :: (a -> m b) -> f a -> m (f b) traverse.traverse :: (a -> m b) -> f (g a) -> m (f (g b)) 

traverse более мощный, чем fmap хотя бы потому что может быть описан с помощью traverse:

fmapDefault :: Traversable t => (a -> b) -> t a -> t b fmapDefault f = runIdentity . traverse (Identity . f) 

Для чего используют Identity? Cмотри ответ здесь

newtype Identity a = Identity { runIdentity :: a }  instance Functor Identity where       fmap f (Identity x) = Identity (f x)  instance Applicative Identity where       pure = Identity       Identity f <*> Identity x = Identity (f x)  instance Monad Identity where       return = pure       Identity x >>= f = f x 

Используя fmapDefault давай сделаем функцию over . over она как fmapDefault только мы передаем traverse тоже:

over :: ((a -> Identity b) -> s -> Identity t) -> (a -> b) -> s -> t over l f = runIdentity . l (Identity . f)  -- over traverse f == fmapDefault f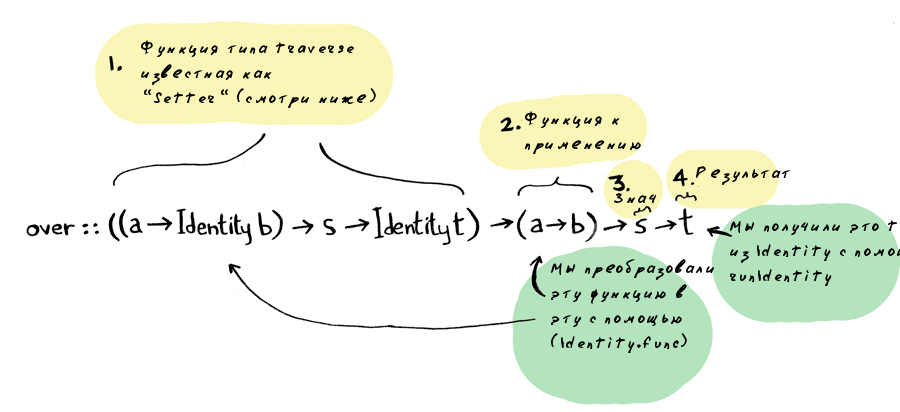 

Мы так близки к линзам! «Ммм я почти общущаю вкус линз Ватсон» расплывается от счастья Шерлок. «Линзы позволяют тебе выполнять композицию функций, fold и обходы (traversals) вместе. Я чувствую как функторы и fold -ы перемешиваются во рту прямо сейчас!»
Я сделаю быстрый псевдоним типа:

type Setter s t a b = (a -> Identity b) -> s -> Identity t 

Теперь можно написать over более чисто:

over :: Setter s t a b -> (a -> b) -> s -> t  -- тоже самое что и: over :: ((a -> Identity b) -> s -> Identity t) -> (a -> b) -> s -> t 

1. over берет Setter
2. и функцию преобразования
3. и значения к которому ее необходимо применить
4. Затем использует сеттер для изменения только части значения с помощью функции

Помните Марио? Теперь это имеет больше смысла:

location.x `over` (+10) $ player1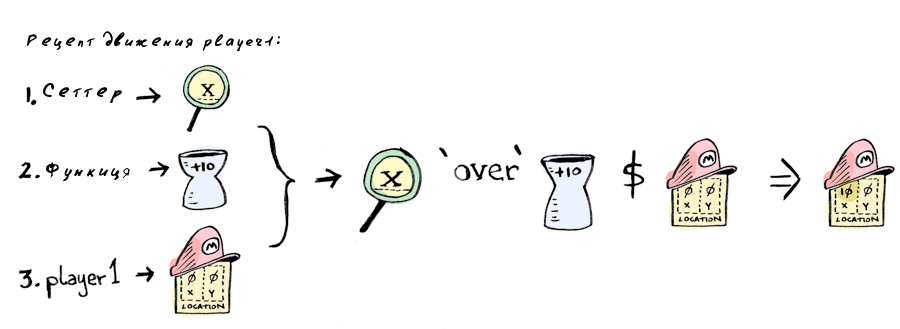 

location.x это сеттер. И знаешь что? location и x сеттеры тоже! Так же как композиция fmap или (.) позволяет тебе «уйти на 1 уровень глубже», ты можешь собрать сеттеры и пойти на один уровень в твоих вложенных данных. Прекрасно!

Fold-ы

Итак мы на один шаг ближе к созданию линз. Мы только что создали сеттеры, которые позволяют нам выполнять композицию функций. Так вышло, мы можем делать тоже самое с fold-ми. Во-первых, определим foldMapDefault:

foldMapDefault :: (Traversable t, Monoid m) => (a -> m) -> t a -> m foldMapDefault f = getConst . traverse (Const . f) 

Что делает Const ?

Это очень похоже на наше определене fmapDefault выше! Мы пришли к тому, что делаем новый псевдоним Fold:

type Fold s t a b = forall m. Monoid m => (a -> Const m b) -> s -> Const m t 

Что очень похоже на Setter:

type Setter s t a b = (a -> Identity b) -> s -> Identity t 

Смотреть полный вывод Fold (на англ.)

Так как сигнатуры Fold и Setter похожи, мы должны иметь возможность собрать их в один псевдоним типа. И мы действительно можем!

type Lens s t a b = forall f. Functor f => (a -> f b) -> s -> f t 

Линзы

Setter -ы для функторов и Fold -ы для fold ов, но линзы более обощенный тип. Они позволяют собирать функторы функции fold ы и traversal ы вместе. Вот например:

Ненавидишь ли ты когда делаешь fmap по паре (tuple) и он задевает только вторую часть?

> fmap (+10) (1, 2) (1,12) 

Что если ты хочешь применить к обеим частями! Напиши линзу!

> both f (a,b) = (,) <$> f a <*> f b 

И используй ее:

> both `over` (+10) $ (1, 2) (11,12) 

И линзы могут быть составлены чтобы пойти глубже! Вот мы применяем функцию к обеим частям обеих частей.

И используйте их:

> (both . both) `over` (+2) $ ((1, 2), (3, 4)) ((3,4),(5,6)) 

И мы можем собрать их с сеттерами или foldми

Заключение

Линзы могут быть очень полезными если у вас много вложенных данных. Их вывод имеет очень интересные части тоже. Полный вывод (на англ).

Шерлок трескает линзы.