Несколько месяцев назад мы получили заказ на автоматизацию процесса оценки качества сыпучего строительного материала (в интересах заказчика законспирируем, какого конкретно, да это и неважно для данной статьи). Задача автоматизации оценки качества не новая, ее уже давно пытаются решать и с успехом решают, но ни один из существующих способов в чистом виде нам не подошел, т.к. каждый из них работает с определенными материалами. В частности существуют способы распознавания и оценки апельсинов (тоже нужная вещь), строения клеток, да и для оценки характеристик различных почв также есть немало способов. Среди всего этого многообразия мы, увы, ничего для своего материала не нашли.
О том, как мы искали свой алгоритм, рассказываем на примере керамзита.
Характеристики частиц почвы определяются с помощью эмпирического метода Krumbein & Sloss, основным инструментом при работе с которым является следующая классическая таблица:

Фото частиц, или непосредственно сами частицы распределяются по ячейкам таблицы и затем считаются средние значение сферичности и окатанности (Sphericity & Roundness).
Перед нашими разработчиками встала задача автоматизации процесса подсчета этих характеристик.
Этапы работы
1. Предобработка
Как все привыкли делать, с самого начала изображение избавляется от шумов с помощью медианного фильтра, затем выравниваются яркостные гистограммы и выправляется контрастность. Это позволяет избежать излишней чувствительности и шумов при бинаризации.
2. Построение бинарной маски
Для оценки формы по таблице Krumbein & Sloss используются четкие контуры объектов.
Задача — их получить.
Проблемы с которыми мы столкнулись: серые частицы на белом фоне или стекле давали тень, слипались друг с другом или просто сливались со своей же тенью.

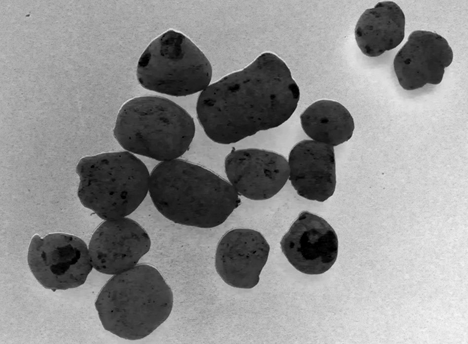
Рис 1. Исходное изображение
Было перепробовано множество способов морфологического анализа контуров, применены различные операторы поиска контуров, границ и пиков энтропии. Ни один из них не дал нужного результата.
Например, воспользовавшись методом Otsu для бинаризации и применив к результату последовательно несколько операций морфологического открытия, закрытия и эрозии, мы могли видеть следующий результат:

Рис 2. Бинарная маска с применением морфологических операций
Светлые промежутки на объектах появились вследствие того, что частицы были в этих частях светлее или вспышка фотоаппарата дала блик.
Бинарная маска получена некачественно, нужно избавиться от мелких белых областей.
Казалось бы, тут нам на помощью пришел бы анализ площади белых областей, мелкие — залить, крупные участки белого фона — оставить. Но не тут-то было. Некоторые частицы лежали близко друг к другу группами по 3. Если избавимся от всех бликов, то исчезнут и ключевые области между частицами (на Рис 2 обведено красным).
Размер областей одинаковый, применить фильтр не вышло. И тут нас осенило: король-то голый частицы-то непрозрачные! А значит можно немного усложнить жизнь пользователю, поставив условие применить цветной фон при съемке, но при этом решить задачу построения маски с гораздо большей точностью. Так и сделали. Вместо градаций серого взяли разницу между красной и зеленой компонентами.
 |
 |
| Рис 4.1. Изображение в градациях серого | Рис 4.2. Бинарная маска, построенная по градациям серого |
 |
 |
| Рис 5.1 Инвертированная разница компонент Red-Green | Рис 5.2 Бинарная маска, построенная по разнице компонент Red-Green |
Как видно, бинарные маски, полученные с помощью метода Отсу, различаются точностью в тех областях, где падает тень от объектов. Если немного изменить порог бинаризации вручную, то результат будет одинаковым. Но плюс и одновременно минус метода Отсу для разделения изображения на два класса состоит в том, что порог бинаризации определяется автоматически. А так как нужно было определять порог разделения без участия пользователя, то был выбран именно этот метод.
3. Как разделить частицы
Как видно на снимке, далеко не все частицы лежат отдельно, здесь нам на помощь приходит метод водораздела (watershed).
Мы использовали Marker-controlled watershed segmentation, базируясь на этом описании http://www.mathworks.com/products/image/examples.html?file=/products/demos/shipping/images/ipexwatershed.html.
Строим евклидово расстояние по бинарной маске.

Рис 6. Euclidean distance
Дополняем маркерами

Рис 6. Евклидово расстояние, совмещенное с маркерами
Применяем к изображению с маркерами метод водораздела.

Рис 7. Области «водораздела»
4. Характеристики
Формулы для характеристики частиц были подсмотрены в этой статье: Particle Shape Determination by Two-Dimensional Image Analysis in Geotechnical Engineering. Rodriguez, J.M. Johansson, J.M.A. Edeskär, T.
Перебрав все формулы, решили остановиться на этом:


6. Ключевым порогом качества в оценке формы частиц считается значение 0.8.
Те частицы, значение параметра R (roundness) или S (sphericity) ниже заданного порога, помечаются на снимке красными лейблами.

Рис 8. Результат вычисления
7. OpenCV
Прототип готов, но чтобы получить реальное приложение, доступное пользователям через веб, надо перейти от алгоритмического прототипа к его воплощению в коде. Для того чтобы реализовать эти алгоритмы на сервере, мы выбрали OpenCV (ссылка на OpenCV). Обычно мы не сталкивались с проблемами реализации алгоритмов обработки изображений с помощью этой библиотеки. Но здесь столкнулись со следующим нюансом: Алгоритм водораздела, реализованный в OpenCV, даёт значительные искажения вдоль границ разделения частиц.

Такие искажения вносят существенную ошибку в определение параметров сферичности и окатанности. Таким образом, такая реализация алгоритма разделения нам не подошла.

Рис 10. OpenCV watershed

Рис 9. Наша альтернатива watershed
В итоге мы отдали предпочтение более простому алгоритму.
Суть использованного нами алгоритма:
1. Находим центр масс маркера. Положение маркера соответствует внутренней области соответствующей частицы. То же справедливо и для центра масс маркера.
2. Движемся вдоль прямой, параллельной оси x и проходящей через центр масс маркера, до точки, имеющей цвет фона: получаем расстояние R от центра масс маркера до границы частицы или их скопления.
3. Последовательно изменяя угол наклона прямой ϕ от 0 до 2π, получим функцию зависимости расстояния от угла R(ϕ). Скачки данной функции – это потенциальные точки разделения.
4. Следующий шаг – найти пороги, определяющие то, какие пиксели считать точками разделения. Первый порог определяет величину скачка функции, второй – максимальное расстояние, на котором скачок функции может считаться точкой разделения. Величины этих порогов зависят от взаимного расположения маркеров разных частиц и для каждого маркера будут свои.

Возможный случай разделения
5. При правильно рассчитанных пороговых значениях скачка функции R(ϕ ) количество точек разделения будет четным. Знак первого обнаруженного скачка определяет порядок соединения точек разделения.
Построенный алгоритм показал нужный результат на наших изображениях. Следующим этапом он был встроен в веб-приложение, с помощью которого специалисты, осуществляющие анализ и оценку характеристик частиц на фото, уже больше не должны были считать эти характеристики вручную.
В ходе поиска решения были проведены поиски на просторах интернета и найдены интересные ссылки по данной теме:
stackoverflow.com/questions/11294859/how-to-define-the-markers-for-watershed-in-opencv
luispedro.org/projects/nuclear-segmentation
ссылка на оригинал статьи http://habrahabr.ru/company/eastbanctech/blog/190198/
Добавить комментарий