SavePearlHarbor

Алгоритм генерации судоку

—

от автора

admin
sudoku250title
Доброго времени суток!

Думаю, головоломка Судоку не нуждается в представлении. Многие из нас проводят за её решением достаточно много времени. Например, когда нужно убить время в дороге или просто поворочать мозги, чтобы не сохли. На хабре есть довольно много постов о решении головоломки. Но когда человек решает с десяток, а может и сотню головоломок, то найдётся пытливый ум, который задаст себе вопрос «А как же получается таблица Судоку, имеющая единственное решение? И как можно описать алгоритм для сетки 9×9?».

Приведённый алгоритм является вполне логичным. Но моей задачей было описание и реализация. Обо всём этом написано под катом.

Основные правила Судоку

  1. Цифра может появиться только один раз в каждой строчке
  2. Цифра может появиться только один раз в каждом столбике
  3. Цифра может появиться только один раз в каждом районе (Район — меньший квадрат со стороной 3х3, на изображении ниже выделен фиолетовым цветом)

Шаг 1. Взять за основу базовую сетку

Сетка должна подчинятся правилам Судоку. Размещаем в первую строку 1 2… 8 9, в строках ниже смещаем на 3 позиции влево, т.е. 4 5… 2 3 и 7 8… 5 6.
Далее переходя в следующий район по вертикали смещаем на 1 позицию влево предыдущий район.

В итоге должна получиться вот такая сетка, её я и назову базовой:

Для реализации создадим класс grid. Заполним его в соответствии с Шагом 1, в котором table — список значений таблицы, метод show — просто наглядный вывод таблицы.

class grid: 	def __init__(self,n = 3): 		"""Generation of the base table""" 		self.n = n 		self.table = [[((i*n + i/n + j) % (n*n) + 1) for j in range(n*n)] for i in range(n*n)] 		print "The base table is ready!"  	def __del__(self): 		pass 	 	def show(self): 		for i in range(self.n*self.n): 			print self.table[i]

Шаг 2. Перетасовать сетку

Есть несколько видов перестановок, выполнив которые таблица Судоку останется в допустимом состоянии.
К ним относятся:

  • Транспонирование всей таблицы — столбцы становятся строками и наоборот (transposing)

  • Обмен двух строк в пределах одного района (swap_rows_small)
  • Обмен двух столбцов в пределах одного района (swap_colums_small)

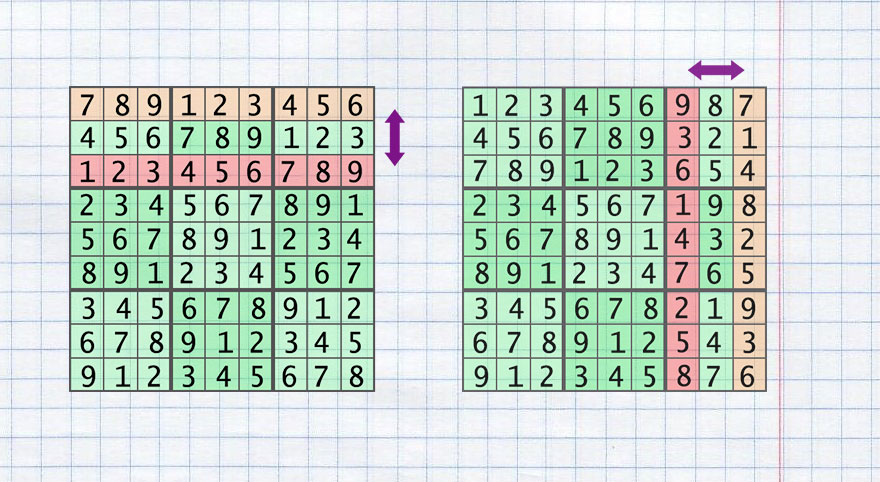
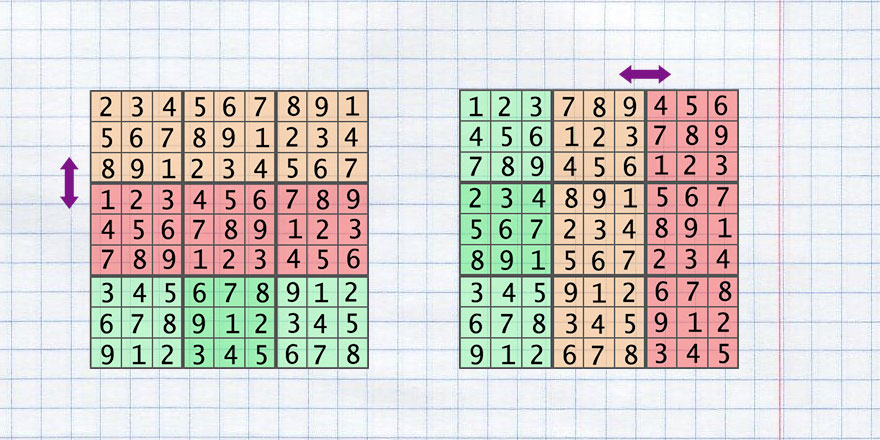
  • Обмен двух районов по горизонтали (swap_rows_area)
  • Обмен двух районов по вертикали (swap_colums_area)

Для каждой из перестановок напишем метод:

transposing

	def transposing(self): 		""" Transposing the whole grid """ 		self.table = map(list, zip(*self.table))

swap_rows_small

	def swap_rows_small(self): 		""" Swap the two rows """ 		area = random.randrange(0,self.n,1) 		line1 = random.randrange(0,self.n,1) 		#получение случайного района и случайной строки 		N1 = area*self.n + line1 		#номер 1 строки для обмена  		line2 = random.randrange(0,self.n,1) 		while (line1 == line2): 			line2 = random.randrange(0,self.n,1)  		N2 = area*self.n + line2 		#номер 2 строки для обмена  		self.table[N1],self.table[N2] = self.table[N2], self.table[N1]

swap_colums_small

Для обмена столбцов можно поменять строки у транспонированной таблицы: 

	def swap_colums_small(self): 		grid.transposing(self) 		grid.swap_rows_small(self) 		grid.transposing(self)

swap_rows_area

	def swap_rows_area(self): 		""" Swap the two area horizon """ 		area1 = random.randrange(0,self.n,1) 		#получение случайного района  		area2 = random.randrange(0,self.n,1) 		while (area1 == area2): 			area2 = random.randrange(0,self.n,1)  		for i in range(0, self.n): 			N1, N2 = area1*self.n + i, area2*self.n + i 			self.table[N1], self.table[N2] = self.table[N2], self.table[N1]

swap_colums_area

	def swap_colums_small(self): 		grid.transposing(self) 		grid.swap_rows_area(self) 		grid.transposing(self)

Может быть есть ещё более сложные преобразования, но, думаю, можно ограничиться этими. Этот каркас инвариантен своей структуре, такие перестановки есть почти тоже самое, что и действия над матрицами относительно определителя или вращение Кубика Рубика.

Теперь, для того чтобы получить случайную комбинацию, достаточно запустить в случайном порядке функции перемешивания. Так и поступим, amt — количество перемешиваний: 

	def mix(self,amt = 10): 		mix_func = ['self.transposing()',  					'self.swap_rows_small()',  					'self.swap_colums_small()',  					'self.swap_rows_area()',  					'self.swap_colums_area()'] 		for i in xrange(1, amt): 			id_func = random.randrange(0,len(mix_func),1) 			eval(mix_func[id_func])

Пример 10 итераций перемешивания

base [1, 2, 3, 4, 5, 6, 7, 8, 9] [4, 5, 6, 7, 8, 9, 1, 2, 3] [7, 8, 9, 1, 2, 3, 4, 5, 6] [2, 3, 4, 5, 6, 7, 8, 9, 1] [5, 6, 7, 8, 9, 1, 2, 3, 4] [8, 9, 1, 2, 3, 4, 5, 6, 7] [3, 4, 5, 6, 7, 8, 9, 1, 2] [6, 7, 8, 9, 1, 2, 3, 4, 5] [9, 1, 2, 3, 4, 5, 6, 7, 8]  swap_colums_area [7, 8, 9, 4, 5, 6, 1, 2, 3] [1, 2, 3, 7, 8, 9, 4, 5, 6] [4, 5, 6, 1, 2, 3, 7, 8, 9] [8, 9, 1, 5, 6, 7, 2, 3, 4] [2, 3, 4, 8, 9, 1, 5, 6, 7] [5, 6, 7, 2, 3, 4, 8, 9, 1] [9, 1, 2, 6, 7, 8, 3, 4, 5] [3, 4, 5, 9, 1, 2, 6, 7, 8] [6, 7, 8, 3, 4, 5, 9, 1, 2]  swap_colums_small [7, 8, 9, 4, 5, 6, 2, 1, 3] [1, 2, 3, 7, 8, 9, 5, 4, 6] [4, 5, 6, 1, 2, 3, 8, 7, 9] [8, 9, 1, 5, 6, 7, 3, 2, 4] [2, 3, 4, 8, 9, 1, 6, 5, 7] [5, 6, 7, 2, 3, 4, 9, 8, 1] [9, 1, 2, 6, 7, 8, 4, 3, 5] [3, 4, 5, 9, 1, 2, 7, 6, 8] [6, 7, 8, 3, 4, 5, 1, 9, 2]  swap_colums_small [7, 8, 9, 4, 5, 6, 1, 2, 3] [1, 2, 3, 7, 8, 9, 4, 5, 6] [4, 5, 6, 1, 2, 3, 7, 8, 9] [8, 9, 1, 5, 6, 7, 2, 3, 4] [2, 3, 4, 8, 9, 1, 5, 6, 7] [5, 6, 7, 2, 3, 4, 8, 9, 1] [9, 1, 2, 6, 7, 8, 3, 4, 5] [3, 4, 5, 9, 1, 2, 6, 7, 8] [6, 7, 8, 3, 4, 5, 9, 1, 2]  transposing [7, 1, 4, 8, 2, 5, 9, 3, 6] [8, 2, 5, 9, 3, 6, 1, 4, 7] [9, 3, 6, 1, 4, 7, 2, 5, 8] [4, 7, 1, 5, 8, 2, 6, 9, 3] [5, 8, 2, 6, 9, 3, 7, 1, 4] [6, 9, 3, 7, 1, 4, 8, 2, 5] [1, 4, 7, 2, 5, 8, 3, 6, 9] [2, 5, 8, 3, 6, 9, 4, 7, 1] [3, 6, 9, 4, 7, 1, 5, 8, 2]  swap_colums_small [7, 1, 4, 8, 2, 5, 6, 3, 9] [8, 2, 5, 9, 3, 6, 7, 4, 1] [9, 3, 6, 1, 4, 7, 8, 5, 2] [4, 7, 1, 5, 8, 2, 3, 9, 6] [5, 8, 2, 6, 9, 3, 4, 1, 7] [6, 9, 3, 7, 1, 4, 5, 2, 8] [1, 4, 7, 2, 5, 8, 9, 6, 3] [2, 5, 8, 3, 6, 9, 1, 7, 4] [3, 6, 9, 4, 7, 1, 2, 8, 5]  swap_rows_small [7, 1, 4, 8, 2, 5, 6, 3, 9] [8, 2, 5, 9, 3, 6, 7, 4, 1] [9, 3, 6, 1, 4, 7, 8, 5, 2] [5, 8, 2, 6, 9, 3, 4, 1, 7] [4, 7, 1, 5, 8, 2, 3, 9, 6] [6, 9, 3, 7, 1, 4, 5, 2, 8] [1, 4, 7, 2, 5, 8, 9, 6, 3] [2, 5, 8, 3, 6, 9, 1, 7, 4] [3, 6, 9, 4, 7, 1, 2, 8, 5]  swap_rows_small [7, 1, 4, 8, 2, 5, 6, 3, 9] [8, 2, 5, 9, 3, 6, 7, 4, 1] [9, 3, 6, 1, 4, 7, 8, 5, 2] [5, 8, 2, 6, 9, 3, 4, 1, 7] [4, 7, 1, 5, 8, 2, 3, 9, 6] [6, 9, 3, 7, 1, 4, 5, 2, 8] [2, 5, 8, 3, 6, 9, 1, 7, 4] [1, 4, 7, 2, 5, 8, 9, 6, 3] [3, 6, 9, 4, 7, 1, 2, 8, 5]  swap_rows_area [7, 1, 4, 8, 2, 5, 6, 3, 9] [8, 2, 5, 9, 3, 6, 7, 4, 1] [9, 3, 6, 1, 4, 7, 8, 5, 2] [2, 5, 8, 3, 6, 9, 1, 7, 4] [1, 4, 7, 2, 5, 8, 9, 6, 3] [3, 6, 9, 4, 7, 1, 2, 8, 5] [5, 8, 2, 6, 9, 3, 4, 1, 7] [4, 7, 1, 5, 8, 2, 3, 9, 6] [6, 9, 3, 7, 1, 4, 5, 2, 8]  swap_colums_small [7, 1, 4, 8, 2, 5, 6, 9, 3] [8, 2, 5, 9, 3, 6, 7, 1, 4] [9, 3, 6, 1, 4, 7, 8, 2, 5] [2, 5, 8, 3, 6, 9, 1, 4, 7] [1, 4, 7, 2, 5, 8, 9, 3, 6] [3, 6, 9, 4, 7, 1, 2, 5, 8] [5, 8, 2, 6, 9, 3, 4, 7, 1] [4, 7, 1, 5, 8, 2, 3, 6, 9] [6, 9, 3, 7, 1, 4, 5, 8, 2]

Шаг 3. Удаление клеток

После полученного решения нам необходимо получить задачу (именно в такой последовательности мы можем гарантировать однозначность решения). И это самая сложная часть. Какое количество можно убрать, чтобы гарантировать однозначность решения? Это один из важных факторов, от которого зависит сложность Судоку. Всего в Судоку 81 клетка, обычно считают лёгким когда на поле есть 30-35 «подсказок», средним — 25-30, и сложным — 20-25. Это данные большого набора реальных примеров, нет никаких законов для сложности. Можно сделать 30-клеточный неразрешимый вариант и 22 клеточный «лёгкий».

  • Случайный подход — можно попробовать выкинуть 50-60 клеток наугад, но где вероятность что Судоку можно будет решить? Например, если заполнены 3 строки ( = 27 клеток)
  • Случайно с простым ограничением — для примера можно взять некое число N в качестве предела, так что N строк и столбцов могут быть пустыми. Принимая N = 0 — для лёгких уровней, N=1 — средний, N=2 — сложный

Итак, приступим к вычёркиванию ячеек (все варианты равнозначны, поэтому у нас 81 ячейка, которую можно вычеркнуть, поэтому проверим все перебором):

  1. Выбрать случайную ячейку N
  2. Отметить N просмотренной
  3. Удалить N
  4. Посчитать решения. Если оно не единственное, то вернуть N обратно

На выходе получится самая сложная из возможных вариантов Судоку для данного перемешивания. Переменная difficult оценивает сложность — количество оставшихся элементов.

 flook = [[0 for j in range(example.n*example.n)] for i in range(example.n*example.n)] iterator = 0 difficult = example.n ** 4 #Первоначально все элементы на месте  while iterator < example.n ** 4: 	i,j = random.randrange(0, example.n*example.n ,1), random.randrange(0, example.n*example.n ,1) # Выбираем случайную ячейку 	if flook[i][j] == 0:	#Если её не смотрели 		iterator += 1 		flook[i][j] = 1 	#Посмотрим  		temp = example.table[i][j]	#Сохраним элемент на случай если без него нет решения или их слишком много 		example.table[i][j] = 0 		difficult -= 1 #Усложняем, если убрали элемент  		table_solution = [] 		for copy_i in range(0, example.n*example.n): 			table_solution.append(example.table[copy_i][:]) #Скопируем в отдельный список  		i_solution = 0 		for solution in solver.solve_sudoku((example.n, example.n), table_solution): 			i_solution += 1 #Считаем количество решений  		if i_solution != 1: #Если решение не одинственное -- вернуть всё обратно 			example.table[i][j] = temp 			difficult += 1  #Облегчаем  example.show() print "difficult = ",difficult
sudoku_generator.py

# coding=utf-8 import random import solver  class grid: 	def __init__(self,n = 3): 		""" Generation of the base table """ 		self.n = n 		self.table = [[ ((i*n + i/n + j) % (n*n) + 1) for j in range(n*n)] for i in range(n*n)] 		print "The base table is ready!"  	def __del__(self): 		pass 	 	def show(self): 		for i in range(self.n*self.n): 			print self.table[i]  	def transposing(self): 		""" Transposing the whole grid """ 		self.table = map(list, zip(*self.table))  	def swap_rows_small(self): 		""" Swap the two rows """ 		area = random.randrange(0,self.n,1) 		line1 = random.randrange(0,self.n,1) 		#получение случайного района и случайной строки 		N1 = area*self.n + line1 		#номер 1 строки для обмена  		line2 = random.randrange(0,self.n,1) 		#случайная строка, но не та же самая 		while (line1 == line2): 			line2 = random.randrange(0,self.n,1)  		N2 = area*self.n + line2 		#номер 2 строки для обмена  		self.table[N1],self.table[N2] = self.table[N2], self.table[N1]   	def swap_colums_small(self): 		grid.transposing(self) 		grid.swap_rows_small(self) 		grid.transposing(self)   	def swap_rows_area(self): 		""" Swap the two area horizon """ 		area1 = random.randrange(0,self.n,1) 		#получение случайного района  		area2 = random.randrange(0,self.n,1) 		#ещё район, но не такой же самый 		while (area1 == area2): 			area2 = random.randrange(0,self.n,1)  		for i in range(0, self.n): 			N1, N2 = area1*self.n + i, area2*self.n + i 			self.table[N1], self.table[N2] = self.table[N2], self.table[N1]   	def swap_colums_area(self): 		grid.transposing(self) 		grid.swap_rows_area(self) 		grid.transposing(self) 	 	def mix(self,amt = 10): 		mix_func = ['self.transposing()',  					'self.swap_rows_small()',  					'self.swap_colums_small()',  					'self.swap_rows_area()',  					'self.swap_colums_area()'] 		for i in xrange(1, amt): 			id_func = random.randrange(0,len(mix_func),1) 			eval(mix_func[id_func])  example = grid() example.mix()  flook = [[0 for j in range(example.n*example.n)] for i in range(example.n*example.n)] iterator = 0 difficult = example.n ** 4 #Первоначально все элементы на месте  example.show()  print "---------------------------"  while iterator < example.n ** 4: 	i,j = random.randrange(0, example.n*example.n ,1), random.randrange(0, example.n*example.n ,1) # Выбираем случайную ячейку 	if flook[i][j] == 0:	#Если её не смотрели 		iterator += 1 		flook[i][j] = 1 	#Посмотрим  		temp = example.table[i][j]	#Сохраним элемент на случай если без него нет решения или их слишком много 		example.table[i][j] = 0 		difficult -= 1 #Усложняем если убрали элемент  		table_solution = [] 		for copy_i in range(0, example.n*example.n): 			table_solution.append(example.table[copy_i][:]) #Скопируем в отдельный список  		i_solution = 0 		for solution in solver.solve_sudoku((example.n, example.n), table_solution): 			i_solution += 1 #Считаем количество решений  		if i_solution != 1: #Если решение не одинственное вернуть всё обратно 			example.table[i][j] = temp 			difficult += 1 # Облегчаем  example.show() print "difficult = ",difficult

solver.py

#!/usr/bin/env python3  # Author: Ali Assaf <ali.assaf.mail@gmail.com> # Copyright: (C) 2010 Ali Assaf # License: GNU General Public License <http://www.gnu.org/licenses/>  from itertools import product  def solve_sudoku(size, grid):     """ An efficient Sudoku solver using Algorithm X.      >>> grid = [     ...     [5, 3, 0, 0, 7, 0, 0, 0, 0],     ...     [6, 0, 0, 1, 9, 5, 0, 0, 0],     ...     [0, 9, 8, 0, 0, 0, 0, 6, 0],     ...     [8, 0, 0, 0, 6, 0, 0, 0, 3],     ...     [4, 0, 0, 8, 0, 3, 0, 0, 1],     ...     [7, 0, 0, 0, 2, 0, 0, 0, 6],     ...     [0, 6, 0, 0, 0, 0, 2, 8, 0],     ...     [0, 0, 0, 4, 1, 9, 0, 0, 5],     ...     [0, 0, 0, 0, 8, 0, 0, 7, 9]]     >>> for solution in solve_sudoku((3, 3), grid):     ...     print(*solution, sep='\\n')     [5, 3, 4, 6, 7, 8, 9, 1, 2]     [6, 7, 2, 1, 9, 5, 3, 4, 8]     [1, 9, 8, 3, 4, 2, 5, 6, 7]     [8, 5, 9, 7, 6, 1, 4, 2, 3]     [4, 2, 6, 8, 5, 3, 7, 9, 1]     [7, 1, 3, 9, 2, 4, 8, 5, 6]     [9, 6, 1, 5, 3, 7, 2, 8, 4]     [2, 8, 7, 4, 1, 9, 6, 3, 5]     [3, 4, 5, 2, 8, 6, 1, 7, 9]     """     R, C = size     N = R * C     X = ([("rc", rc) for rc in product(range(N), range(N))] +          [("rn", rn) for rn in product(range(N), range(1, N + 1))] +          [("cn", cn) for cn in product(range(N), range(1, N + 1))] +          [("bn", bn) for bn in product(range(N), range(1, N + 1))])     Y = dict()     for r, c, n in product(range(N), range(N), range(1, N + 1)):         b = (r // R) * R + (c // C) # Box number         Y[(r, c, n)] = [             ("rc", (r, c)),             ("rn", (r, n)),             ("cn", (c, n)),             ("bn", (b, n))]     X, Y = exact_cover(X, Y)     for i, row in enumerate(grid):         for j, n in enumerate(row):             if n:                 select(X, Y, (i, j, n))     for solution in solve(X, Y, []):         for (r, c, n) in solution:             grid[r][c] = n         yield grid  def exact_cover(X, Y):     X = {j: set() for j in X}     for i, row in Y.items():         for j in row:             X[j].add(i)     return X, Y  def solve(X, Y, solution):     if not X:         yield list(solution)     else:         c = min(X, key=lambda c: len(X[c]))         for r in list(X[c]):             solution.append(r)             cols = select(X, Y, r)             for s in solve(X, Y, solution):                 yield s             deselect(X, Y, r, cols)             solution.pop()  def select(X, Y, r):     cols = []     for j in Y[r]:         for i in X[j]:             for k in Y[i]:                 if k != j:                     X[k].remove(i)         cols.append(X.pop(j))     return cols  def deselect(X, Y, r, cols):     for j in reversed(Y[r]):         X[j] = cols.pop()         for i in X[j]:             for k in Y[i]:                 if k != j:                     X[k].add(i)  if __name__ == "__main__":     import doctest     doctest.testmod()

Результат работы

The base table is ready! [5, 4, 6, 8, 7, 9, 2, 1, 3] [8, 7, 9, 2, 1, 3, 5, 4, 6] [2, 1, 3, 5, 4, 6, 8, 7, 9] [6, 5, 7, 9, 8, 1, 3, 2, 4] [9, 8, 1, 3, 2, 4, 6, 5, 7] [3, 2, 4, 6, 5, 7, 9, 8, 1] [7, 6, 8, 1, 9, 2, 4, 3, 5] [1, 9, 2, 4, 3, 5, 7, 6, 8] [4, 3, 5, 7, 6, 8, 1, 9, 2] --------------------------- [0, 0, 6, 0, 0, 0, 0, 0, 0] [8, 7, 0, 0, 1, 0, 0, 0, 6] [0, 0, 0, 5, 4, 0, 0, 0, 9] [6, 0, 0, 0, 8, 1, 3, 0, 4] [0, 0, 0, 3, 0, 0, 0, 5, 0] [0, 0, 0, 0, 0, 7, 0, 0, 0] [0, 0, 0, 0, 0, 0, 0, 0, 0] [0, 9, 0, 4, 0, 0, 0, 0, 8] [0, 0, 5, 0, 6, 0, 1, 0, 0] difficult =  22

Скачать в zip

Я уверен, что есть и более сложные подходы в построении таблицы Судоку. Моя цель была достигнута, получился рабочий алгоритм. Теперь мне не нужно искать новые выпуски, я могу их генерировать 🙂
В принципе, здесь был приведён частный случай Судоку 9х9. Но нет ограничений для использования его на 16х16 и 25х25.

Если у кого есть лучшие предложения — не стесняйтесь оставить комментарий.
Спасибо за внимание.

ссылка на оригинал статьи http://habrahabr.ru/post/192102/

Комментарии

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *