В статье уже был кратко рассмотрен оператор LBP. Хотелось бы остановиться на данном вопросе несколько подробнее, а также рассмотреть применение LBP к решению задачи распознавания лиц.
1. Введение
Как правило, система распознавания лиц представляет собой программно-аппаратный комплекс для автоматической верификации или идентификации личности по цифровому изображению (фотографии или кадру видеопоследовательности). Задача распознавания лиц решается при разработке систем контроля и управления доступом, систем пограничного контроля, проведении оперативно-розыскных мероприятий и т.д.
В процессе распознавания лиц возникает ряд сложностей, связанных с изменением условий освещения, вращением головы, возрастными изменениями и проч. Можно выделить следующие основные этапы процесса верификации и идентификации:
- регистрация и нормализация изображения;
- выбор признаков;
- вычисление меры близости;
- построение решающего правила.
Основными целями данной работы являлись разработка и анализ алгоритма распознавания лиц на основе локальных бинарных шаблонов (ЛБШ). Укажем основные этапы решения поставленной задачи:
- предобработка (нормализация) изображения;
- построение вектора признаков;
- выбор меры близости;
- построение решающего правила;
- тестирование и сравнение различных подходов.
2. Локальные бинарные шаблоны
Локальный бинарный шаблон – это определенный вид признака, используемый для классификации в компьютерном зрении, и представляющий собой простой оператор. Локальные бинарные шаблоны впервые были предложены в 1996 году для анализа текстуры полутоновых изображений. При этом дальнейшие исследования показали, что ЛБШ инвариантны к небольшим изменениям в условиях освещения и небольшим поворотам изображения [1].
ЛБШ представляет собой описание окрестности пикселя изображения в двоичном представлении. Базовый оператор ЛБШ, применяемый к пикселю изображения, использует восемь пикселей окрестности, принимая значение интенсивности центрального пикселя в качестве порога (рисунок 2.1). Пиксели со значением интенсивности большим или равным значению интенсивности центрального пикселя принимают значения равные «1», остальные принимают значения равные «0». Таким образом, результатом применения базового оператора ЛБШ к пикселю изображения является восьмиразрядный бинарный код, который описывает окрестность этого пикселя [1].
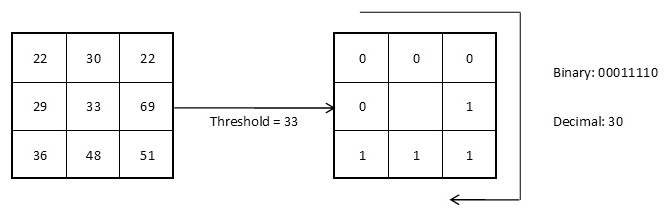 |
| Рисунок 2.1 — Базовый оператор ЛБШ |
Использование круговой окрестности и билинейной интерполяции значений интенсивностей пикселей позволяет построить локальный бинарный шаблон с произвольным количеством точек P и радиусом R (рисунок 2.2) [1-4].
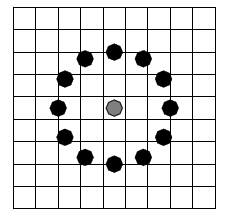 |
| Рисунок 2.2 – Расширенный оператор ЛБШ |
Некоторые бинарные коды несут в себе больше информации, чем остальные. Так, локальный бинарный шаблон называется равномерным, если он содержит не более трех серий «0» и «1» (например, 00000000, 001110000 и 11100001). Во-первых, равномерные ЛБШ определяют только важные локальные особенности изображения, такие как концы линий, грани, углы и пятна (рисунок 2.3). Во-вторых, они обеспечивают существенную экономию памяти (P(P-1)+2 различных шаблонов вместо 2P).
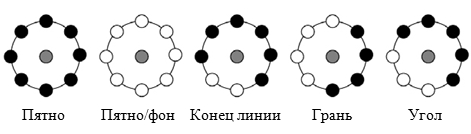 |
| Рисунок 2.3 – Примеры локальных особенностей, детектируемых РЛБШ |
3. Гистограмма ЛБШ
Применяя оператор ЛБШ к каждому пикселю изображения, мы можем построить гистограмму, в которой каждому равномерному коду ЛБШ соответствует отдельный столбец. Также имеется еще один дополнительный столбец, который содержит информацию обо всех неравномерных шаблонах.
Изображения лиц могут рассматриваться как набор всевозможных локальных особенностей, которые хорошо описываются с помощью локальных бинарных шаблонов. Однако гистограмма, построенная для всего изображения в целом, кодирует лишь наличие тех или иных локальных особенностей, но при этом не содержит никакой информации об их расположении на изображении. Для учета такого рода информации изображение разбивается на подобласти, в каждой из которых вычисляется своя гистограмма ЛБШ (рисунок 3.1). Путем конкатенации этих гистограмм может быть получена общая гистограмма, учитывающая как локальные, так и глобальные особенности изображения [2,3].
 |
| Рисунок 3.1 – Разбиение изображения лица на подобласти |
При таком подходе для лучшего извлечения признаков можно варьировать параметры оператора ЛБШ и число разбиений изображения на подобласти.
4. Построение решающего правила
В ходе работы исследовались три подхода к вычислению меры различия гистограмм двух сопоставляемых изображений и построению соответствующего решающего правила.
4.1. Взвешенное расстояние Кульбака-Лейблера
Некоторые подобласти изображения могут содержать более важную информацию, чем остальные, и в соответствии с этим каждой из них можно назначить свой весовой коэффициент. Так, например, веса могут быть получены с помощью критерия Стьюдента, заключающегося в проверке гипотезы о различиях между двумя выборками, по обучающим данным, представляющих два класса («свои» и «чужие» в случае решения задачи верификации или идентификации).
В качестве меры различия двух гистограмм использовалось взвешенное расстояние Кульбака-Лейблера в симметричной форме:
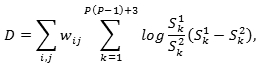 |
(4.1) |
где (i,j) – индексы подобласти изображения, wij – весовой коэффициент подобласти, S1,S2 – гистограммы ЛБШ первого и второго изображений соответственно, k – номер столбца гистограммы ЛБШ, P – число точек окрестности в шаблоне ЛБШ.
При этом задача идентификации решалась с использованием классификатора по методу ближайшего соседа, а задача верификации – путем пороговой классификации.
4.2. Расстояние Махаланобиса
Данный подход заключается в использовании расстояния Махаланобиса:
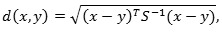 |
(4.2) |
где x,y – случайные векторы с одинаковым распределением и корреляционной матрицей S.
Корреляционная матрица S может быть получена с использованием обучающей выборки изображений. Определяя расстояние Кульбака-Лейблера (4.1) для каждой из подобластей изображений, мы можем получить вектор различий двух изображений. Вычисляя такие вектора для каждой пары изображений обучающей выборки, мы получим два набора векторов различий изображений, соответствующих двум классам – классу «своих» и классу «чужих». После этого мы можем вычислить средние значения векторов, представляющих каждый из классов, а также две корреляционные матрицы.
На практике, для любых двух изображений мы можем вычислить их вектор различий, а затем определить расстояния Махаланобиса d1 и d2 между этим вектором и средними векторами классов «свой» и «чужой» соответственно. Идентификация и верификация могут быть произведены путем сравнения двух полученных расстояний либо с использованием дискриминирующей функции f(d1,d2 ) = d2⁄(d1+d2) и некоторого порогового значения.
4.3. Применение линейного дискриминанта Фишера
Следующий подход опирается на использование линейного дискриминанта Фишера (ЛДФ):
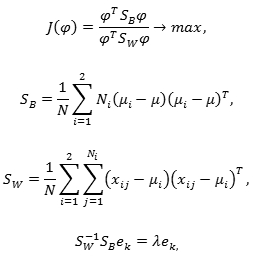 |
(4.3) |
где μi — среднее для i-го класса, μ — общее среднее, Ni — число представителей в i-м классе, N — общее число представителей в обучающей выборке, xij — j-й представитель i-го класса.
Пусть имеется два набора векторов, соответствующих двум классам. Собственный вектор, соответствующий наибольшему собственному значению матрицы Sw-1Sb задает преобразование в пространство размерности 1.
Задача идентификации и верификации может быть решена способом, аналогичным предыдущему (путем построения векторов различий изображений с использованием расстояния Кульбака-Лейблера). При этом вместо расстояния Махаланобиса используется отображение вектора в одномерное пространство.
5. Предобработка изображений
С целью снижения уровня шума использовались медианный и гауссовский фильтры. Кроме того, изображения проходили процедуру нормализации, т.е. кадрировались, масштабировались и доворачивались до горизонтального положения линии, соединяющей центры глаз (рисунок 5.1).
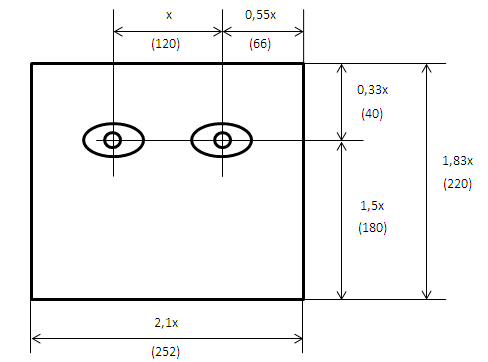 |
| Рисунок 5.1 – Параметры нормализации изображения |
6. Описание и результаты эксперимента
Для обучения и тестирования использовалась база данных ColorFERET.
- обучающая выборка: 100 человек, 5 фотографий на каждого;
- тестовая выборка: 329 человек, 2 фотографии на каждого.
Все алгоритмы были обучены так, чтобы обеспечить значение вероятности ложного допуска (FAR) равным 0,1%. Наилучшие результаты были получены при использовании следующих параметров:
- параметры оператора ЛБШ: P = 8, R = 2;
- число разбиений изображения: 6 × 6 (вдоль осей x и y соответственно).
В таблице 6.1 приведены результаты тестирования разработанных алгоритмов.
| Мера различия | Идентификация на закрытом множестве | Верификация |
| Взвешенное расстояние Кульбака-Лейблера | 89,5 % | 84,2 % |
| Расстояние Махаланобиса | 89,8 % | 80,8 % |
| Преобразование в 1-мерное пространство с помощью ЛДФ | 92,0 % | 86,0 % |
7. Заключение
В данной статье кратко рассмотрен алгоритм построения вектора признаков на основе локальных бинарных шаблонов.
Показано, что использование разных решающих правил для одних и тех же векторов признаков может повысить качество работы системы распознавания лиц. Как видно из таблицы 6.1 наилучшие вероятностные характеристики получены с использованием линейного дискриминанта Фишера.
Кроме того, следует отметить, что качество работы системы существенным образом зависит от предобработки входных изображений. В ходе выполнения работы было отмечено, что отсутствие этапа фильтрации приводит к снижению вероятностей правильной идентификации и верификации.
8. Список использованных источников
- T. Maenpaa. The Local Binary Pattern Approach to Texture Analysis — Extensions and Applications. Oulu University Press, 2003.
- D. Maturana, D. Mery, A. Soto. Face Recognition with Local Binary Patterns, Spatial Pyramid Histograms and Naive Bayes Nearest Neighbor classification. In Proc. of the XXVIII International Conference of the Chilean Computer Science Society, IEEE CS Society, 2009.
- C. Shan, S. Gong, P.W. McOwan. Facial expression based on Local Binary Patterns: A comprehensive study. Image and Vision Computing, (27), 2009.
- T. Ahonen, A. Hadid, M. Pietikainen. Face Recognition with Local Binary Patterns. Lecture Notes in Computer Science, 2004.
P.S. Хотелось бы отдельно отметить, что в дальнейших работах вероятностные характеристики алгоритма верификации и идентификации были несколько улучшены. Это было достигнуто путем построения векторов признаков не только для изображения лица в целом, но и для областей пары глаз, носа и рта, а также существенным увеличением объема обучающей выборки. К сожалению, я не могу более подробно изложить материалы этих исследований, поскольку полученные результаты представляют собой коммерческую тайну.
P.P.S. Данная статья написана на основе другой моей публикации и включает в себя некоторые поправки. Большая просьба при использовании материалов данной статьи (особенно в научных работах) ссылаться на исходную версию:
Петрук В.И., Самородов А.В., Спиридонов И.Н. Применение локальных бинарных шаблонов к решению задачи распознавания лиц. Вестник Московского государственного технического университета им. Н.Э. Баумана. Серия: Приборостроение. 2011. № S. С. 58-63.
ссылка на оригинал статьи http://habrahabr.ru/post/193658/
Добавить комментарий