MatLab предоставляет широкие возможности по отображению графической информации в виде графиков, диаграмм, и т.п. Однако не всегда получаемые по умолчанию иллюстрации удовлетворяют требованиям оформления статей. Для этого в системе MatLab существует множество настроек. И чтобы ускорить подготовку иллюстраций предлагаю воспользоваться несколькими строчками кода, которые помогут помочь настроить отображение графиков.

Прежде всего, необходимо настроить шрифты, которые будут использоваться для вывода значений осей и надписей на графиках, что также помогает в случаях неправильного отображения надписей на русском языке:

set(0,'DefaultAxesFontSize',14,'DefaultAxesFontName','Times New Roman'); set(0,'DefaultTextFontSize',14,'DefaultTextFontName','Times New Roman'); 

Затем необходимо настроить размер графика и его положение на экране, например, с отображением на весь экран:

figure('Units', 'normalized', 'OuterPosition', [0 0 1 1]);

При необходимости вставляем название графика:

title('Название');

Далее можно включить построение нескольких графиков в одном окне, c использованием тех же осей и свойств графика:

hold on;%или hold all;

Строим графики с определенным цветом, стилем и толщиной линии:

plot(X2,Y2,':k','LineWidth',3); plot(X2,Y3,':b','LineWidth',3); plot(X2,Y4,'-.','Color',[.1 .7 .7],'LineWidth',3); plot(X2,Y5,'--','Color',[.1 .4 .1],'LineWidth',3); plot(X2,Y6,'r','LineWidth',3);

Вставляем легенду в график с определенным положением на рисунке, например справа внизу:

legend('исходные данные','полином 3-й степени','полином 4-й степени','полином 5-й степени','полином 7-й степени','полином 9-й степени', 4);

И вот тут начинается самое интересное…

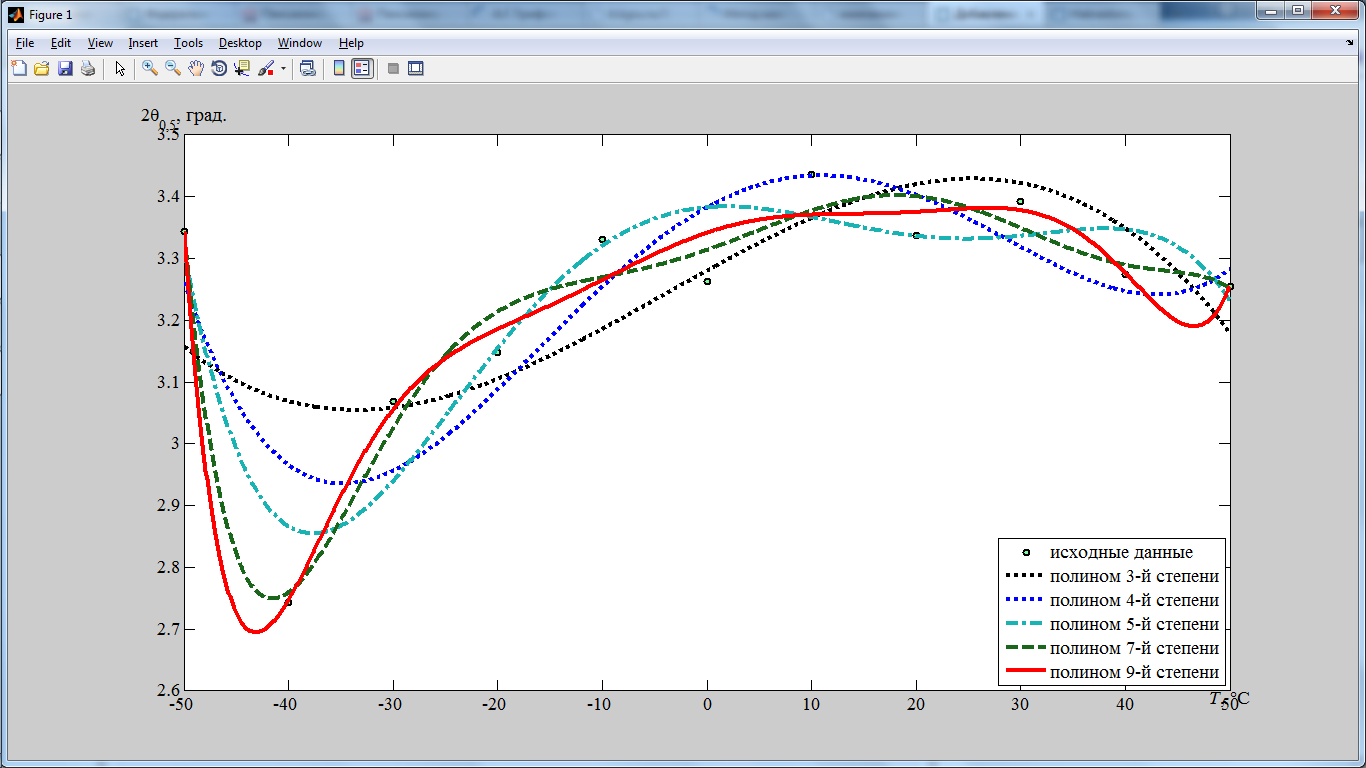
При построении графика в MatLab дробные значения подписей на осях координат отображаются с разделителем в виде точки, тогда как, разделитель дробной и целой части у нас принято отображать запятой.

Чтобы не изменять вручную все значения подписей данных осей через меню графика,

BX=get(gca,'XTick'); BY=get(gca,'YTick');  xlabel(XL,'Position',[BX(size(BX,2)) BY(1)]) ylabel(YL,'Rotation',0,'Position',[BX(1) BY(size(BY,2))])  XA=get(gca,'XTickLabel');%  for i=1:size(XA,1)      z=rem(i,2);     if z==0;         if XA(i,1)~='0' && XA(i,2)~=0             XA(i,:)=char(0);         end     end      end  XA(size(XA,1),:)=char(0);  set(gca,'XTickLabel',XA);  YA=get(gca,'YTickLabel');%  for i=1:size(YA,1)      z=strfind(YA(i,:),'.');     YA(i,z)=',';     clear z;     z=rem(i,2);     if z~=0;          YA(i,:)=char(0);     end      end  YA(size(YA,1),:)=char(0);  set(gca,'YTickLabel',YA);

Код «прореживает» подписи осей x и y, а также исправляет точки на запятые в подписях на оси y. Для других осей необходимо повторить аналогичные процедуры.

И в заключении отобразим линии координатной сетки:

grid on;

Для удобства использования, чтобы не повторять каждый раз эти действия, заключаем написанный код в функцию, в параметрах которой указываются настройки отображения графиков и их данные.

function result=subgraphic(X1,X2,Y1,Y2,Y3,Y4,Y5,Y6,Tit,TL,XL,YL,PL)  figure('Units', 'normalized', 'OuterPosition', [0 0 1 1]);  plot(X1,Y1,'o','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor',[.49 1 .63],'MarkerSize',5);  if Tit      title(TL); end  hold on;  plot(X2,Y2,':k','LineWidth',3);  plot(X2,Y3,':b','LineWidth',3);  plot(X2,Y4,'-.','Color',[.1 .7 .7],'LineWidth',3);  plot(X2,Y5,'--','Color',[.1 .4 .1],'LineWidth',3);  plot(X2,Y6,'r','LineWidth',3);  legend('исходные данные','полином 3-й степени','полином 4-й степени','полином 5-й степени','полином 7-й степени','полином 9-й степени', PL);  BX=get(gca,'XTick'); BY=get(gca,'YTick');  xlabel(XL,'Position',[BX(size(BX,2)) BY(1)]) ylabel(YL,'Rotation',0,'Position',[BX(1) BY(size(BY,2))])  XA=get(gca,'XTickLabel');%  for i=1:size(XA,1)      z=rem(i,2);     if z==0;         if XA(i,1)~='0' && XA(i,2)~=0             XA(i,:)=char(0);         end     end      end  XA(size(XA,1),:)=char(0);  set(gca,'XTickLabel',XA);  YA=get(gca,'YTickLabel');%  for i=1:size(YA,1)      z=strfind(YA(i,:),'.');     YA(i,z)=',';     clear z;     z=rem(i,2);     if z~=0;          YA(i,:)=char(0);     end      end  YA(size(YA,1),:)=char(0);  set(gca,'YTickLabel',YA);  grid on;  result=1;

Выполним

subgraphic(B,T,A,Y3,Y4,Y5,Y7,Dva_theta_0_5,Tit,'Название','{\itT}, \circC','{2{\phi}_{0,5}, град.',3); 

с заранее подготовленными данными.

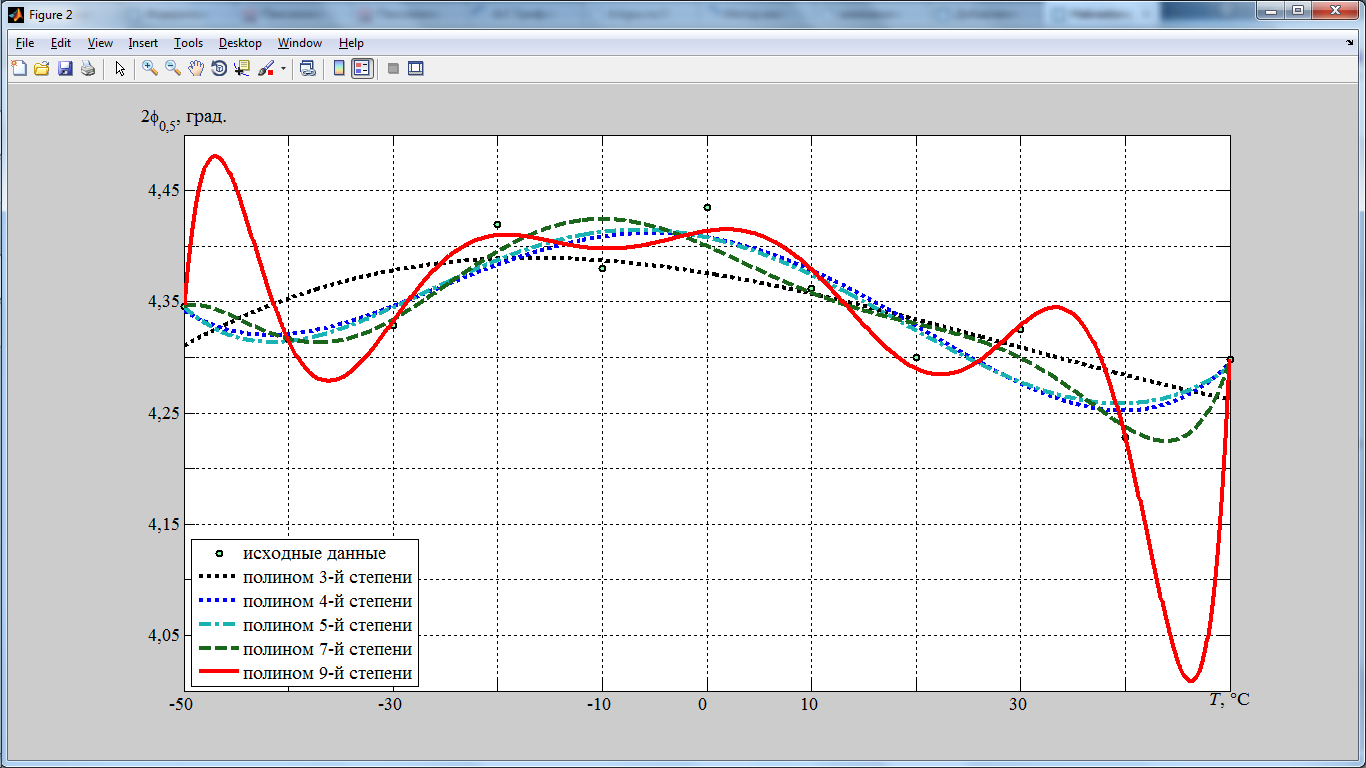
По умолчанию MatLab отображает греческую букву «фи» как в кириллице «ф». Одним из способов отобразить привычную греческую букву «фи» с петлеобразным начертанием, является выбор специального шрифта c греческими буквами. Скачиваем, например, шрифт Greek Normal отсюда и устанавливаем. Просмотрев шрифт Greek в таблице символов, замечаем, что в этом шрифте буква «фи» существует в двух вариантах, причем для кода латинской «f» получим тот же результат что и в MatLab в виде «ф», а для кода латинской «j» должен быть получен требуемый результат.

Выполним

subgraphic(B,T,A,Y3,Y4,Y5,Y7,Dva_theta_0_5,Tit,'Название','{\itT}, \circC','{2\fontname{Greek}j}_{0,5}, град.',3);

И получим вот такой график:

В результате использования приведенного кода для построения графиков с помощью системы MatLab удалось:

• Решить проблему с некорректным отображением кириллических шрифтов;
• Автоматически заменить разделитель целой и дробной части числа с точки на запятую в графике;
• Отобразить греческую букву фи в петлеобразном начертании.

PS Если кто-то знает простой способ отобразить символ греческой буквы «фи» с кодом unicode-03С6 в графиках MatLab, напишите пожалуйста в комментариях.

И несколько полезных ссылок:
Код на Github.com
Некоторые полезные средства настройки графиков (plot) в MATLAB
Заметки про Matlab. Экспорт графиков.
Простейшее приложение с GUI средствами MatLab 6.5