Количество ложно-положительных срабатываний фильтра Блума [перевод]

Количество ложно-положительных срабатываний фильтра Блума.

Описание

Фильтр Блума — это рандомизированная структура данных для запросов, разработанная Бёртоном Блумом в 1970 году. Фильтр Блума даёт ошибочный ответ на запрос, т.н. ложно-положитеное срабатывание. Т.е. если мы добавляем некоторый элемент, то существует отличная от нуля вероятность, что фильтр Блума вернет ответ что элемент находится в векторе, хотя его там нет.

Грубо говоря, фильтр Блума возвращает 2 возможных ответа:

1. элемента нет в векторе
2. элемент возможно есть в векторе

Блум проанализировал вероятность таких ошибочных ответов, но его анализ является некорректным.

В статье я не буду описывать построение фильтра Блума, об этом можно прочитать в соответствующей статье Фильтр Блума или на вики WIKI: Фильтр Блума

Введение

Фильтр Блума представляет собой структуру данных, которая отображает множество S из n элементов в битовый вектор 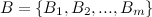. Для записи элемента используются k-случайных хэш-функций, таких что 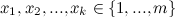. Изначально вектор инициализируется нулями. Запись элемента производится путем установки в единицу всех k-бит в векторе B, т.е. . Для проверки существования элемента 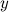в фильтре достаточно узнать значения каждого k-бита вектора. Если есть хотя бы один ноль, то это значит что такого элемента ещё в векторе нет, а если все биты установлены в единицу, это говорит о том, что элемент вероятно уже существует. Эта ситуация называется ложно-положительным срабатыванием.

Блум посчитал ложно-положительные срабатывания следующим образом:
Вероятность, что любой бит вектора B равен нулю — это 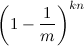после установки всех единиц k-хэш-функций при добавлении n-элементов.
По этому, вероятность что конкретный бит будет установлен в единицу это

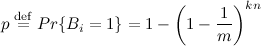
Теперь, что бы привести 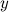к ложно-положительным срабатываниям, каждый из k-битов вектора 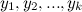должен быть установлен в единицу. Вероятность этого:

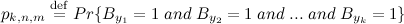
которая, как утверждается равна

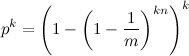
Это доказательство, которое появилось много лет назад некорректное. Ошибка кроется в том, что делается неявное предположение, что событие 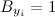и событие 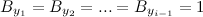считаются независимыми. На первый взгляд это похоже на правда, так как 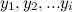независимы. Однако, простой контрпример к доказательству может быть получен учитывая случай 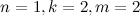. В этом случае при простом перечисление 16 возможных ситуаций обнаруживается вероятность ложно-положительного срабатывания как 5/8, в то время как формула Блума даёт результат 9/16 = 4.5/8

Точная формула

Смоделируем проблему определения количества ложно-положительных срабатываний как проблему шаров и корзин. У нас есть m-корзин. Мы бросаем kn белых шаров в случайные корзины. Мы можем считать корзину белой, если она содержит хотя бы один белый шар. Дальше мы помещаем k-черных шаров в корзины. Пусть событие A состоит в том, что каждый черный шар расположен в белой корзине. Посчитаем вероятность этого события .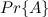
Заметим что множество белый корзиночек может быть представлено как подмножество 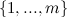. Для любого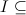 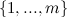обозначим 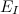как событие состоящее в том, что I — это множество белых корзин. Мощность I равна 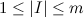. Воспользуемся формулой условной вероятности:

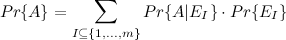
Если I фиксированно, то

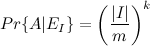
, где 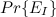содержит в себе

• количество отображений из множества размера kn во множество значений i и
• количество функций из множества размера kn во множество размера m

Количество отображений из множества размера kn во множество размера i описывается формулой 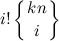, где

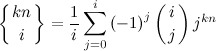
Количество функций из множества размера kn во множество размера m это .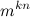

Объединяем эти формулы:

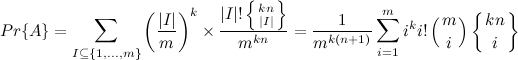
Итоговый результат

Итоговый результат получается, что вероятность ложно-положительных срабатываний фильтра Блума из m бит при добавлении n элементов, используя k-хэш-функций равна:

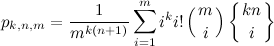
Эта формула уже не является такой простой как было изначально рассчитано Блумом. Не вдаваясь в дальнейшие подробности, скажу что авторы статьи описывают так же верхнюю и нижнюю границы этой формулы и приходят к выводу что начальную формулу, которую вывел Блум можно использовать только как нижнюю границу.

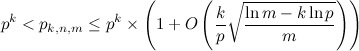
Текст оригинальной статьи:
ON THE FALSE-POSITIVE RATE OF BLOOM FILTERS