Но иногда приятнее найти совсем нестандартное решение.
Пример. Задача 9. Найти пифагорейский триплет целых чисел a, b, c, такой что a + b + c = 1000. Напомню, пифагорейский триплет — это три целых положительны числа a < b < c, являющиеся сторонами прямоугольного треугольника, т.е. a^2 + b^2 = c^2. Самый известный школьный пример: 3, 4, 5.
Переборное решение очевидно. Она сильно сокращается по времени, если знать свойства таких триплетов, можно много итераций сэкономить. Но мы пойдем другим путем.
Будем использовать для решения оптимизационный инструмент Solver в комплекте MS Excel любой версии.
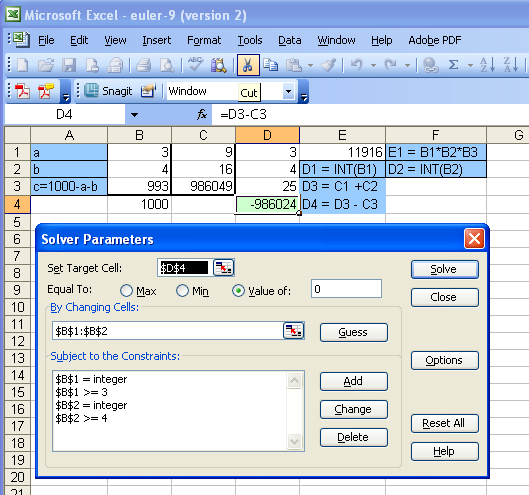
Solver может быть очень мощным инструментом поиска решения, хотя говорят, что в очень многомерных случаях он пасует. До сих пор вспоминаю картину, когда я увидел человека, искавшего Solver-ом решение или хотя бы локальное приближение для огромной системы уравнений на несколько десятков переменных. Писал для магистерского диплома, что-то по экономике. Он точно мог бы написать код на любом из нескольких языков, но было в лом. Поставил настройки в Solver на огромное максималное число итераций, огромное максимальое время поиска и запустил на своем компе на работе. Что-то там насчитал в результате.
Кстати, Solver мне не удалось приткнуть для решения задачи о максимальной сумме пути — там совсем негладкая получается функция, случайная.
Несколько задачек, как я говорил, удалось решить без кода, аналитически. Один раз пришлось посчитать биномиальный коэффициент, для этого использовал инженерный калькулятор Windows. Одна задача в конце первой сотне решилась с помощью SQL — надо было только скопировать данные в табличу — регулярка в Notepad++, создающая DDL скрипт, после чего заполнение таблицы и запрос в одну строку.
Очень улекательно также посмотреть на статистику projectEuler. Максимально эффективные используемые языки и среды — не C++\Java, а французский матпакет PARI/GP, Mathematics, Python и Haskel. Используется множество экзотических (статистика на момент написания поста):
| Language | Number of Users | Average Percent Solved | Score Index | |
|---|---|---|---|---|
| 1 | PARI/GP | 79 | 23% | 99 |
| 2 | Mathematica | 1272 | 13% | 92 |
| 3 | Python | 26887 | 8% | 81 |
| 4 | Haskell | 4680 | 8% | 67 |
| 5 | Sage | 180 | 12% | 62 |
| 6 | Perl | 2237 | 8% | 61 |
| 7 | C/C++ | 28454 | 6% | 61 |
| 8 | APL/J/K | 254 | 11% | 60 |
| 9 | Java | 18158 | 6% | 58 |
| 10 | C# | 9122 | 6% | 54 |
| 11 | ML | 436 | 9% | 54 |
| 12 | Maple | 265 | 9% | 49 |
| 13 | Ruby | 4229 | 6% | 49 |
| 14 | Scala | 1270 | 7% | 49 |
| 15 | MUMPS | 22 | 16% | 49 |
| 16 | LISP | 1096 | 7% | 48 |
| 17 | Delphi | 451 | 8% | 48 |
| 18 | F# | 936 | 7% | 47 |
| 19 | Scheme | 744 | 7% | 46 |
| 20 | Matlab | 2122 | 6% | 45 |
| 21 | Magma | 21 | 15% | 45 |
| 22 | Racket | 140 | 9% | 44 |
| 23 | Component Pascal | 7 | 22% | 42 |
| 24 | BASIC | 1162 | 6% | 42 |
| 25 | Go | 414 | 7% | 41 |
| 26 | Frink | 10 | 18% | 41 |
| 27 | Clojure | 991 | 6% | 41 |
| 28 | D | 163 | 8% | 40 |
| 29 | Pencil/Paper | 805 | 6% | 39 |
| 30 | Pascal | 601 | 6% | 38 |
| 31 | Tcl | 65 | 9% | 37 |
| 32 | R | 496 | 6% | 37 |
| 33 | RPL | 14 | 14% | 36 |
| 34 | Spreadsheet | 412 | 6% | 35 |
| 35 | GAP | 26 | 11% | 35 |
| 36 | Assembly | 152 | 7% | 34 |
| 37 | Lua | 332 | 6% | 34 |
| 38 | Fortran | 308 | 6% | 34 |
| 39 | Forth | 39 | 9% | 32 |
| 40 | Smalltalk | 90 | 7% | 31 |
| 41 | SAS | 17 | 10% | 28 |
| 42 | Ada | 97 | 6% | 27 |
| 43 | ECMAScript | 834 | 4% | 26 |
| 44 | Q | 74 | 6% | 25 |
| 45 | Erlang | 580 | 4% | 25 |
| 46 | Julia | 36 | 7% | 24 |
| 47 | AutoHotkey | 12 | 10% | 24 |
| 48 | Prolog | 114 | 5% | 23 |
| 49 | PHP | 2445 | 3% | 23 |
| … | … | … | … | … |
| 53 | Octave | 63 | 5% | 20 |
| 54 | Boo | 17 | 7% | 19 |
| 55 | Cobra | 3 | 18% | 19 |
| 56 | Logo | 26 | 6% | 19 |
| 57 | Groovy | 38 | 5% | 18 |
| 58 | SQL | 37 | 5% | 17 |
| 59 | COBOL | 19 | 6% | 17 |
| 60 | PowerShell | 68 | 4% | 16 |
| … | … | … | … | … |
| 68 | Bourne Shell | 32 | 3% | 10 |
| … | … | … | … | … |
Больше всего народу, конечно, из Штатов — около 28 тысяч, из Китая и России примерно одинаковое число — около 3000. Но если ткнуть в страну и посмотреть топ 100 по задачам, видно, что китайцы эффективнее — там больше число людей, решивших, более 400, 350, 300, итд. задач. А в Индии наоборот — участников примерно в 2.5 раза больше, но супер-решателей поменьше, чем в РФ. По-моему если нормализовать это все на число населения, то начиная с какого-то статистически значимого числа участников на страну можно получить оценку эффективности высшего образования в ней.
ссылка на оригинал статьи http://habrahabr.ru/post/196966/
Добавить комментарий