Доброго времени суток. В процессе разработки одного из методов кластеризации, возникла у меня потребность визуализировать гауссиан (нарисовать эллипс по сути) на плоскости по заданной ковариационной матрице. Но я как-то сразу и не задумался, что за простой отрисовкой обычного эллипса по 4 числам скрываются какие то трудности. Оказалось, что при расчете точек эллипса используются собственные числа и собственные векторы ковариационной матрицы, расстояние Махаланобиса, а так же квантили распределение хи-квадрат, которое я, честно говоря, не использовал со времен университета ни разу.
Данные и их взаимное расположение
Давайте начнем с начальных условий. Итак, мы имеем некоторый массив двумерных данных
для которого мы можем легко узнать ковариационную матрицу и средние значения (центр будущего эллипса):
plot(data[, 1], data[, 2], pch=19, asp=1, col=rgb(0, 0.5, 1, 0.2), xlab="x", ylab="y") sigma <- cov(data) m.x <- mean(data[, 1]) m.y <- mean(data[, 2]) Прежде чем приступить к отрисовке эллипса, нужно определиться с тем, какого размера будет фигура. Вот несколько примеров:
Для определения размера эллипса вспомним расстояние Махаланобиса между двумя случайными векторами из одного вероятностного распределения с ковариационной матрицей Σ:
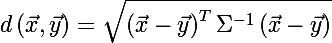
Так же можно определить расстояние от случайного вектора x до множества со средним значением μ и ковариационной матрицей Σ:
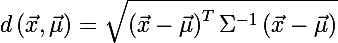
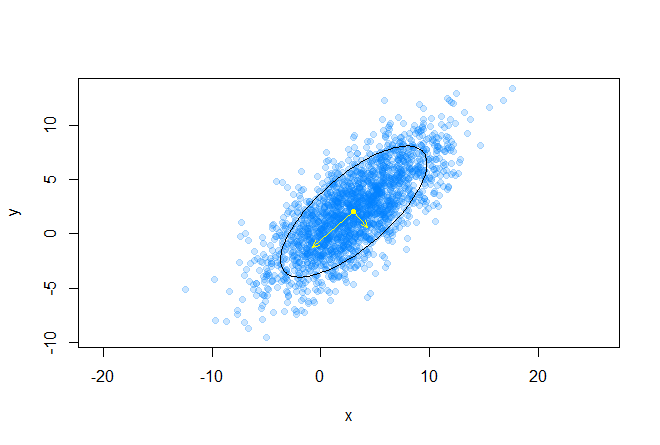
Стоит заметить, что в случае, когда Σ равна единичной матрице, расстояние Махаланобиса вырождается в Евклидово расстояние. Смысл расстояния Махаланобиса в том, что оно учитывает корреляцию между переменными; или другими словами, учитывается разброс данных относительно центра масс (предполагается, что разброс имеет форму эллипсоида). В случае же использования Евклидова расстояния, используется предположение, что данные распределены сферически (равномерно по всем измерениям) вокруг центра масс. Проиллюстрируем это следующим графиком:
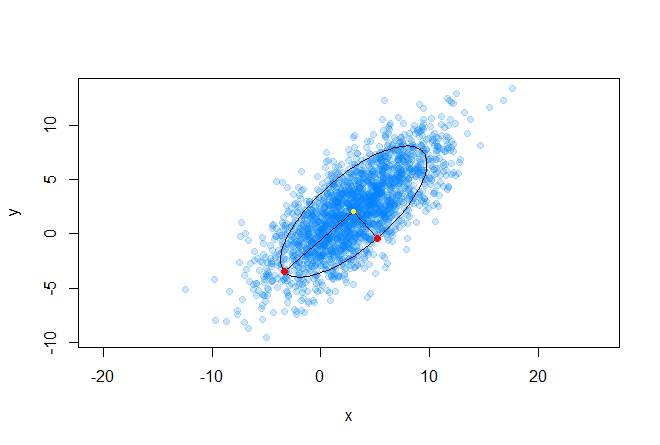
Желтым цветом отмечен центр масс, а две красные точки из набора данных, расположенные на главных осях эллипса, находятся на одинаковом, в смысле Махаланобиса, расстоянии от центра масс.
Эллипс и распределение хи-квадрат
Эллипс является центральной невырожденной кривой второго порядка, его уравнение можно записать в общем виде (ограничения выписывать не будем):
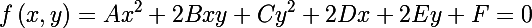
С другой стороны, можно записать уравнение эллипса в матричной форме (в однородных двумерных координатах):
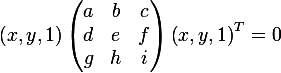
и получить следующее выражение, для того, чтобы показать, что в матричной форме действительно задан эллипс:
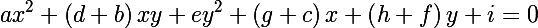
Теперь вспомним расстояние Махаланобиса, и рассмотрим его квадрат:
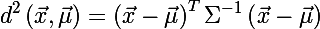
Легко заметить, что это представление идентично записи уравнения эллипса в матричной форме. Таким образом, мы убедились, что расстояние Махаланобиса описывает эллипс в Евклидовом пространстве. Расстояние Махаланобиса — это просто расстояние между заданной точкой и центром масс, делённое на ширину эллипсоида в направлении заданной точки.
Наступает тонкий момент для понимания, у меня это заняло некоторое время, что бы осознать: квадрат расстояния Махаланобиса это сумма квадратов k-ого количества нормально распределенных случайных величин, где n — это размерность пространства.
Вспомним, что такое распределение хи-квадрат — это распределение суммы квадратов k независимых стандартных нормальных случайных величин (это распределение параметризируется количеством степеней свободы k). А это как раз и есть расстояние Махаланобиса. Таким образом вероятность того, что x находится внутри эллипса выражается следующей формулой:
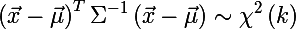
И вот мы пришли к ответу на вопрос о размере эллипса — его размер мы будем детерминировать квантилямираспределения хи-квадрат, это легко делается в R (где q из (0, 1) и k — количество степеней свободы):
v <- qchisq(q, k) Получение контура эллипса
Идея генерации контура нужного нам эллипса очень проста, мы просто возьмем ряд точек на единичной окружности, сместим эту окружность в центр масс массива данных, затем масштабируем и растянем эту окружность в нужных направлениях. Рассмотрим геометрическую интерпретацию многомерного гауссового распределения: как мы знаем, это эллипсоид, у которого направление главных осей задано собственными значениями ковариационной матрицы, а относительная длина главных осей задана корнем из соответствующих собственных значений.
На следующем графике изображены собственные векторы ковариационной матрицы масштабированные на корни из соответствующих собственных значений, направления соответствуют главным осям эллипса:
Рассмотрим разложение ковариационной матрицы в следующем виде:
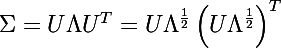
где U — матрица образованная единичными собственными векторами матрицы Σ, а Λ — диагональная матрица, составленная из соответствующих собственных значений.
e <- eigen(sigma) А также рассмотрим следующее выражение для случайного вектора из многомерного нормального распределения:
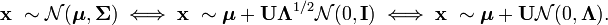
Таким образом, распределение N(μ, Σ) — это, по сути, стандартное многомерное нормальное распределение N(0, I) масштабированное на Λ^(1/2), повернутое на U и смещенное на μ.
Давайте теперь напишем функцию, которая рисует эллипс, со следующими входными данными:
- m.x, m.y — координаты центра масс
- sigma — ковариационная матрица
- q — квантиль распределения хи-квадрат
- n — плотность дискретизации эллипса (количество точек по которым будет строится эллипс)
GetEllipsePoints <- function(m.x, m.y, sigma, q = 0.75, n = 100) { k <- qchisq(q, 2) # вычисляем значение квантиля sigma <- k * sigma # масштабирование ковариационной матрицы на значение квантиля e <- eigen(sigma) # вычисление собственных значений масштабированной ковариационной матрицы angles <- seq(0, 2*pi, length.out=n) # разбиваем круг на n-ое количество углов cir1.points <- rbind(cos(angles), sin(angles)) # генерируем точки на единичной окружности ellipse.centered <- (e$vectors %*% diag(sqrt(abs(e$values)))) %*% cir1.points # масштабируем и поворачиваем полученный датасет ellipse.biased <- ellipse.centered + c(m.x, m.y) # смещаем его до центра масс return(ellipse.biased) # готово } Результат
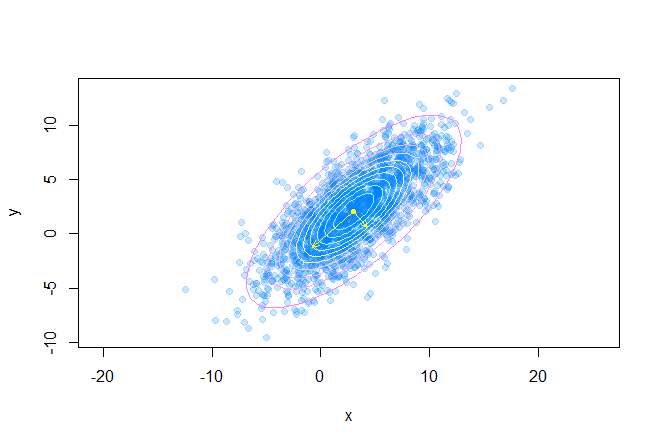
Следующий код рисует множество доверительных эллипсов вокруг центра масс датасета:
points(m.x, m.y, pch=20, col="yellow") q <- seq(0.1, 0.95, length.out=10) palette <- cm.colors(length(q)) for(i in 1:length(q)) { p <- GetEllipsePoints(m.x, m.y, sigma, q = q[i]) points(p[1, ], p[2, ], type="l", col=palette[i]) } e <- eigen(sigma) v <- (e$vectors %*% diag(sqrt(abs(e$values)))) arrows(c(m.x, m.x), c(m.y, m.y), c(v[1, 1] + m.x, v[1, 2] + m.x), c(v[2, 1] + m.y, v[2, 2] + m.y), В итоге получаем такую картину:
Почитать
Код можно найти у меня на гитхабе.
ссылка на оригинал статьи http://habrahabr.ru/post/199060/
Добавить комментарий