Введение в параллельные вычисления в R

Для дальнейшей работы потребуются два пакета — «foreach» (позволяет использовать конструкцию foreach) и «doSNOW» (обеспечивает поддержку параллельных вычислений). Из CRAN их можно установить так:

install.packages(c("foreach","doSNOW"))

Следующие команды — подготовка «кластера» из трех ядер процессора к работе:

library(foreach) library(doSNOW) cluster <- makeCluster(3, type = "SOCK", outfile="") registerDoSNOW(cluster) 

Рассмотрим пример, где подсчитывается сумма квадратов чисел от 1 до 10000:

system.time ({   sum.par <- foreach(i=1:10000, .combine='+') %dopar% {     i^2 }}) 

В принципе, все очень похоже на обычный цикл, за исключением того, что надо указывать, как группировать результаты — в данном случае это операция сложения (а часто это функции c, rbind, cbind — или же собственноручно написанная функция). Если не важно, в каком порядке группировать, то использование аргумента .inorder=F позволяет несколько ускорить вычисления. Если вместо %dopar% использовать директиву %do%, то вычисления будут выполняться последовательно (т.е. как в обычном цикле). К слову сказать, для такой простой задачи время выполнения в последовательном варианте будет заметно меньше, т.к. накладные раcходы на манипуляции с данными в параллельном варианте занимают далеко не самое последнее место в балансе.

Перейдем к более сложной задаче. Допустим, у нас есть вектор случайных величин х.

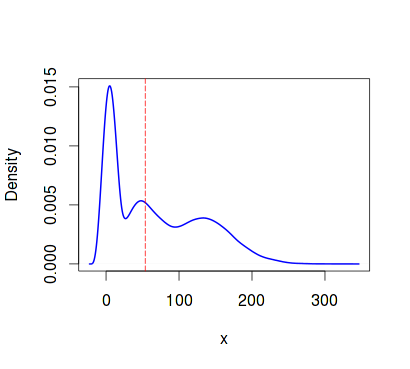
trials <- 10000 n <- 24000 alfa <- 1.6 beta <- 3 set.seed(1) x <- c(rgamma(n/3, shape=alfa, scale=beta),         rgamma(n/3, shape=3*alfa, scale=4*beta),        rgamma(n/3, shape=10*alfa, scale=3*beta)) plot(density(x, kernel="cosine"),lwd=2, col="blue", xlab="x",ylab="Density", main="Density plot") abline(v = median(x), col = "red", lty=5) 

Оценим медиану — с указанием доверительных интервалов. Для этого применим бутстрэп и измерим время выполнения для последовательного кода и параллельного соответственно:

set.seed(1) seq.time <- system.time({   seq.medians <- foreach(icount(trials), .combine=cbind) %do% {     median(sample(x, replace = T))   } }) 

> quantile(seq.medians, c(.025, .975))     2.5%    97.5%  52.56311 54.99636   > seq.time    user  system elapsed   19.884   0.252  20.138 

set.seed(1) par.time <- system.time({   par.medians <- foreach(icount(trials), .combine=cbind) %dopar% {     median(sample(x, replace = T))   } }) 

> quantile(par.medians, c(.025, .975))     2.5%    97.5%  52.56257 54.94890      > par.time    user  system elapsed    4.252   0.420  10.893  

Разница вполне ощутима. Оценим время работы последовательного «векторизированного» варианта для этой же задачи (с применением функции apply):

set.seed(1) seq.time.ap <- system.time({  seq.medians.ap <- apply(matrix(sample(x, trials*n, replace = T), trials, n), 1, median) }) 

> quantile(seq.medians.ap, c(.025, .975))     2.5%    97.5%  52.56284 54.98266     > seq.time.ap    user  system elapsed   23.732   1.728  25.472   

Подобный же подход можно использовать для определения параметров алгоритмов машинного обучения. Например, в пакете «RSNNS» есть функции для обучения сети Элмана (насколько я знаю, в R, в общем-то, нет других пакетов для работы с рекуррентными сетями). Выбор количества нейронов и скорости обучения — довольно ресурсоемкая задача, посему есть смысл в распараллеливании.
Перейдем от сферических примеров к более насущной проблеме. Для этого установим два пакета:

install.packages(c("ElemStatLearn","RSNNS")) 

Из пакета «ElemStatLearn» нам понадобятся два набора данных — zip.train и zip.test, которые содержат сжатые (gzipped) образы рукописных цифр. Датасеты довольно объемные, поэтому возьмем лишь их часть: соответственно для обучения сети, валидации и тестирования.

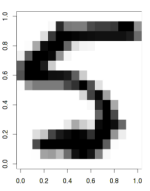
library("ElemStatLearn") library(RSNNS) data(zip.train) data(zip.test)  image(zip2image(zip.train, 1000), col=gray(255:0/255))  train  <- zip.train[1:1000,-1] trainC <- decodeClassLabels(zip.train[1:1000,1])  valid  <- zip.train[1001:1200,-1] validC <- zip.train[1001:1200,1]  test  <- zip.test[1:1000,-1] testC <- zip.test[1:1000,1] 

Прежде чем обучать несколько сетей параллельно, нам надо продумать, что именно мы хотим получить. Допустим, нас интересуют два параметра нейронной сети — количество нейронов в скрытом слое и скорость обучения, и мы хотим подобрать более-менее оптимальные их значения. Значит, результатом работы будет кадр данных, содержащий три числа — количество нейронов, скорость обучения и ошибку, на основе которой мы и будем определять оптимальность параметров. Ранее я упоминал о функции, которая осуществляет группировку результатов работы параллельного цикла. В случае данных, которые имеют более сложную структуру, чем у вектора, такую функцию придется писать самому.

comb <- function(df1, df2) if (df1$err < df2$err) df1 else df2

Как видно из кода, функция сравнивает поле err двух кадров данных и выбирает тот, где ошибка меньше. Ниже непосредственно представлен фрагмент скрипта, который и осуществляет обучение сетей в параллельном режиме. Запускаем его и некоторое время любуемся 100% загрузкой трех ядер.

errCl <- function (predicted, true){   return(round(sum(predicted != true)/length(true), 4)) }    size <- c(13,29,53,71) lr <- c(.001,.01,.1,.5)    nn.time <- system.time({   elm_par <- foreach(s=size, .combine='comb') %:%      foreach(r=lr, .packages='RSNNS', .combine='comb', .inorder=F) %dopar% {       elm <- elman(x=train, y=trainC, size=s, learnFunc="JE_BP", learnFuncParams=r,       linOut=F, maxit=193)       pred <- max.col(predict(elm, valid)) - 1       e <- errCl(pred, validC)       data.frame(opt_size=s, lrate=r, err=e)     }   }) 

Функция errCl используется для определения ошибки классификации. В векторах size и lr содержатся соответственно количества нейронов в скрытом слое сети и скорости обучения сети. Обратите внимание, как организовывается вложенный цикл с помощью инструкции %:%. Собственно, если не вдаваться в подробности, в теле цикла происходит то, что обычно делают при выборе параметров: обучается модель на тренировочном наборе данных, потом используется валидирующий набор данных, определяется ошибка классификации и выбираются те параметры, при которых ошибка меньше. У меня же получился такой результат:

> elm_par     opt_size lrate  err 1   29       0.5    0.05 > nn.time user   system  elapsed  0.312  0.168   179.542  

Хотя, конечно, не стоит обольщаться ошибкой в 5%. Проверим нашу сеть с 29 нейронами и скоростью обучения 0.5 на тестовом наборе:

elm <- elman(x=train, y=trainC, size=29, learnFunc="JE_BP", learnFuncParams=0.5, linOut=F, maxit=193) pred <- max.col(predict(elm, test)) - 1 e <- errCl(pred, testC) 

> e [1] 0.119 

Что же, 11.9% тоже весьма неплохо. Теперь дело осталось за малым — «погасить» кластер

stopCluster(cluster)

Вместо заключения

R — весьма удобный и коварный язык. Привыкнув к нему — и особенно к разнообразию пакетов в CRAN — трудно перейти на что-то другое. Но, безусловно, у каждого языка своя ниша. Для R — это статистика и анализ данных. И хотя R может быть весьма неторопливым, для многих задач его производительности вполне хватает.

Литература

High-Performance and Parallel Computing with R
Nesting Foreach Loops
RSNNS Package