
Из нестандартных правил выделяется довольно интересный режим «узелки», в котором составлять слово можно, используя одну букву до 2-х раз (например, на скриншоте сверху можно составить слово ШАЛАШ, буквы Ш и А использованы 2 раза). Как потом выяснилось, в одной и той же позиции алгоритм ищет все слова в режиме узелки почти ровно в 1.5 раз дольше, чем в классическом режиме без узелков (это и не удивительно, т.к. вариантов составления слов больше и найденные слова длиннее). В конце статьи описанный алгоритм будет протестирован в тестовой позиции в режиме узелки.
Словарь
Для того чтобы ещё больше затруднить жизнь алгоритму будет использоваться один из самых больших словарей в подобных программах. Он насчитывает примерно 110000 слов.
Важную роль в алгоритме играет способ хранения словаря в памяти программы. При загрузке каждое слово записывается в структуру в виде дерева. Каждый узел этого дерева означает конкретную букву слова и ссылается на не более чем 32 поддерева (по количеству букв в алфавите). Узел дерева в программе выглядит так:
typedef TREE *NEXT; //указатель на следующую букву struct TREE { NEXT *next; //массив указателей на все возможные следующие буквы char *str; //строка со всеми возможными следующими буквами char *wrd; //если не NULL, то это слово из словаря }; В поле str содержится строка со всеми буквами, которые выходят из данного узла, размер массива next[] равен длине этой строки.
Поле str используется для нахождения конкретного узла среди массива узлов next[] для данной буквы. Для этого введена функция ind(), основанная на strchr():
int k=ind('и',str); //возвращает индекс (позицию) буквы ‘и’ в строке str Если k<0, то данной буквы нет в str, иначе next[k] указывает на узел, соответствующий этой букве. Например, если str содержит строку "аоикт", то из этого узла идут ровно 5 поддеревьев, причем next[2] ссылается на букву 'и', т.к. str[2]== 'и', то же самое и с другими буквами.
Для иллюстрации всего вышеописанного приведу пример дерева на специально подготовленном словаре, состоящем из слов:
балда, банка, бар, манка, барсук

Если поле str==NULL, то данный узел является листом и в нём содержится словарное слово wrd. Узел, соответствующий букве 'р', содержит слово "бар", и при этом он не является листом, потому что в данном словаре есть ещё одно слово, начинающееся на бар-. Поле wrd содержит строку, которая получается, если идти от корня к соответствующему узлу, но если эта строка не является словарным словом, то wrd содержит NULL.
Назовём это дерево словарным, в нём содержатся все слова из словаря. Помимо словарного дерева необходимо подготовить ещё одно, в котором содержатся все возможные инвертированные префиксы слов для каждого слова (назовём это дерево инвертированным). К примеру, для слова "балда" в инвертированное дерево попадут следующие строки: "адлаб", "длаб", "лаб", "аб", "б". Даже для тестового словаря с пятью словами такое дерево будет громоздким, поэтому приведу упрощенный вариант:
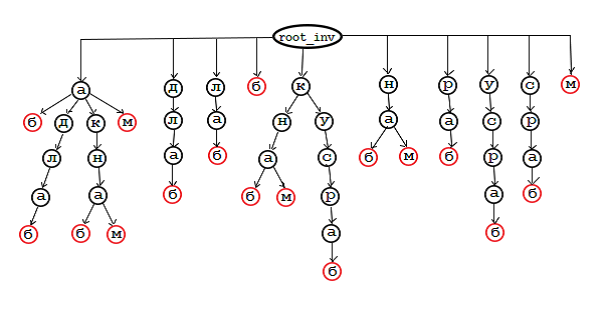
Слова Префиксы словарных слов в этом дереве расположены задом-наперед. Узел в красном кружочке соответствует последней букве инвертированного префикса словарного слова, т.е. соответствует первой букве этого слова. Чтобы прочитать начало словарного слова нужно двигаться от красного узла к корню. Единственное отличие инвертированного дерева от словарного – это то, что wrd выполняет роль флага (NULL/не NULL). Т.е. в нем хранится не строка с инвертированным префиксом слова, а:
- 1) Адрес глобальной строки (содержимое строки не имеет значения), если данный узел соответствует первой букве словарного слова
- 2)
NULL, для всех остальных узлов.
Это сделано для экономии места. Для всех красных узлов wrd!=NULL, для остальных wrd==NULL. К примеру:
root_inv->str == ”адлбкнрусм”; root_inv->next[0]->str == ”бдкм”; root_inv->next[5]->next[0]->wrd == NULL; //АН не является префиксом словарного слова root_inv->next[5]->next[0]->next[1]->wrd != NULL; //МАН является префиксом словарного слова
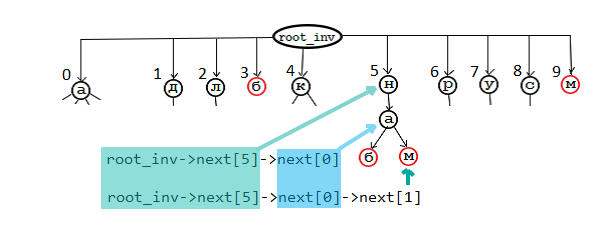
Оба дерева занимают в памяти 33М, и непосредственно из словаря они строятся примерно за 5 секунд на i5, поэтому было принято решение сохранить образ деревьев в файл и в дальнейшем грузить именно его. Так скорость загрузки составила всего 300 миллисекунд.
Алгоритм поиска
По правилам балды для хода нужно выбрать пустую клетку, и поставить туда любую букву.
Затем нужно составить слово, используя поставленную букву. Данная буква может быть как первой буквой в слове, так и не первой буквой (хоть и капитанство, но это важно). Если бы в правилах было сказано, что поставленная буква должна быть точно первой, то просто используем словарное дерево, двигаясь по полю от поставленной буквы одновременно спускаясь вниз по дереву. Но т.к. поставленная буква может и не быть первой, словарное дерево использовать нельзя, потому что не известно с какого именно узла начинать поиск. Но у нас ещё есть инвертированное дерево.
Идея такая: из клетки с поставленной буквой движемся по полю, спускаясь по инвертированному дереву. Если находим узел, у которого wrd!=NULL (красный узел), значит это валидный инвертированный префикс слова. Имея префикс слова, можно в словарном дереве найти узел, соответствующий поставленной букве, и далее просто «донайти» оставшийся кусок слова уже в словарном дереве, начиная с этого узла.
Для того чтобы алгоритм не заходил в клетки, которые ранее для данного слова уже прошёл, в каждой клетке имеется счетчик использования count. Перед началом поиска этот счетчик инициализируется числом 2 (для режима узелки) или 1 (для классического режима) – это единственное отличие режимов с точки зрения алгоритма.
Более подробный алгоритм:
- 1) Перебираем все пустые смежные клетки
- 2) Для каждой клетки перебираем все буквы алфавита (32 буквы)
- 3) Заносим в текущую клетку (пусть её координаты будут
[x, y]) текущую буквуs. Так получаем 32*n разных позиций, где n – число смежных клеток в исходной позиции - 4) Занесенную букву считаем первой буквой для инвертированных префиксов.
Поэтому средиroot_inv->next[]находим узелt_inv, соответствующий текущий букве, т.е.t_inv– поддерево, начинающееся с текущей буквы:
int k = ind(s, root_inv->str); //s – текущая буква if(k<0) continue; //вдруг инвертированный префикс не может начинаться с этой буквы TREE * t_inv = root_inv->next[k]; - 5) Уменьшаем
count[x, y]и вызываем функцию поиска в поддеревеfind(о которой ниже) дляt_invи клетки[x, y] - 6) Конец цикла по буквам
- 7) Конец цикла по смежным клеткам
Естественно после цикла по буквам очищаем текущую смежную клетку.
Функция поиска в поддереве find принимает игровое поле, узел дерева (tree) и координаты клетки (i, j), с которой необходимо начать двигаться по полу, спускаясь по дереву tree:
- 1) Если
tree->wrd!=NULL, то найдена валидная подстрока
- a. Если этот узел принадлежал словарному дереву, то эта подстрока вообще словарное слово, добавляем
tree->wrdв массив найденных слов. - b. Если узел принадлежал инвертированному дереву, то эта подстрока является инвертированным префиксом слова. В словарном дереве находим узел
t, соответствующий этому префиксу, и вызываем функциюfindдляtи клетки[x, y](внимание! Не та клетка, которую передали в эту функцию, а клетка, в которую алгоритм сходил на шаге 3):
TREE *t=root; //корень словарного дерева loopi(strlen(prefix)) //prefix содержит найденный инвертированный префикс { int k=ind(prefix[i],t->str); t=t->next[k]; } find(t,x,y);
- a. Если этот узел принадлежал словарному дереву, то эта подстрока вообще словарное слово, добавляем
- 2) Независимо от значения
tree->wrdпродолжаем - 3) Перебираем клетки, смежные с
[i, j](от 2-х в углу до 4-х в центре поля) - 4) Анализируем содержимое текущей смежной клетки
[i1, j1]
- a. Если она пустая, то переходим на шаг (3)
- b. Если буква, находящаяся в этой клетке, не имеется в
tree->str, то переходим на шаг (3) - c. Если
count[i1, j1]==0, то переходим на шаг (3) - d. Иначе переходим на шаг (5)
- 5) Среди
tree->next[]находим узелtnext, соответствующий букве в[i1, j1] - 6) Уменьшаем счетчик использования
count[i1, j1]и вызываемfindдляtnextи клетки[i1, j1] - 7) Конец цикла по смежным буквам
Рассмотрим работу алгоритма для центральной клетки на примере следующей позиции:

Заносим в эту клетку каждую букву из строки ”адлбкнрусм” (остальные буквы алфавита просто не существуют в root_inv->str и алгоритм для них быстро завершится, даже не начавшись). Для каждой буквы вызываем find. Для буквы А функция быстро завершится, потому что в инвертированном дереве нет веток, начинающихся на АА-, АС- и АКУ-, то же самое и для Д, К, У, С.

Для остальных букв в инвертированном дереве будут найдены валидные префиксы:
Л – лаб, Б – б, Н – наб, Р – раб, М – м. Для каждого префикса находим узел в словарном дереве (как описано в п.1.b) и вызываем для него функцию find.
Префиксу “бал” соответствует узел root->next[0]->next[0]->next[0]:

Следующей смежной буквой может быть С или К, но в поле str этого узла содержится “д”, поэтому сразу завершаем функцию find, т.е. в дереве нет веток, начинающихся на БАЛС- и БАЛК-. Для префикса “б” в словарном дереве нет веток, начинающихся на БК-, БС-, БАБ-, БАЪ-, то же самое и для префиксов “бан” и “м”.

Префиксу “бар” соответствует узел root->next[0]->next[0]->next[2].
Т.к. поле wrd!=NULL, заносим строку wrd (БАР) в массив найденных слов и продолжаем поиск дальше. Для строк БАРК и БАРСЪ нет веток, завершаем для них функцию find, а вот строка БАРСУК содержится в дереве, помещаем её в массив найденных слов.
Результаты
Алгоритм тестировался на следующем поле (естественно уже не на тестовом словаре, а на словаре из 110000 слов):

Это реально игравшаяся партия.
Здесь поле 9х9, и оно наполовину заполнено (пожалуй, это одна из наихудших позиций для любого алгоритма, потому что присутствует достаточно много клеток, куда можно сходить, и достаточно удачное взаимное расположение букв, из-за чего много длинных слов можно составить). В режиме узелки алгоритм находит все слова за следующее время:
- 1) Mac mini i7 – 7 миллисекунд (не нативное приложение, а в эмуляторе iPhone)
- 2) Комп. с i5 – 12 миллисекунд
- 3) iPad 4 – 30 миллисекунд
- 4) Samsung Galaxy Ace (железо трёхлетней давности) – 50 миллисекунд (с использованием NDK)
Для других позиций время поиска еще меньше.
Приложение
Данный алгоритм применен в приложениях для iOS (доступно в app store) и Android. Помимо поиска всех слов реализованы ещё два вида поиска:
- 1) Локальный поиск – если пользователю позарез нужно занять какую-либо определённую пустую клетку (например, призовая клетка, или прикрыть своим ходом клетку, в которой слишком много длинных слов), тогда он делает двойной тап по этой клетке и программа ищет только те слова, которые можно сходить в неё
- 2) Проверка подстав – двойной тап по букве заставит программу найти все слова, проходящие через эту букву. Применение: сразу после хода соперника проверить его букву (вдруг он жестко подставился), перед своим ходом следует проверить предполагаемый ход на предмет подстав
Ещё одна особенность: одинаковые по длине слова сортируются по редкости добавляемой буквы (например, сходить буквой Ч выгоднее, чем буквой А).
ссылка на оригинал статьи http://habrahabr.ru/post/207734/
Добавить комментарий