Splay-деревья

Сбалансированное дерево поиска является фундаментом для многих современных алгоритмов. На страницах книг по Computer Science вы найдете описания красно-черных, AVL-, B- и многих других сбалансированных деревьев. Но является ли перманентная сбалансированность тем Святым Граалем, за которым следует гоняться?

Представим, что мы уже построили дерево на 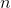ключах и теперь нам нужно отвечать на запросы, лежит ли заданный ключ в дереве. Может так оказаться, что пользователя интересует в основном один ключ, и остальные он запрашивает только время от времени. Если ключ лежит далеко от корня, то 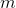запросов могут отнять 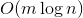времени. Здравый смысл подсказывает, что оценку можно оптимизировать до 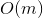, надстроив над деревом кэш. Но этот подход имеет некоторый недостаток гибкости и элегантности.

Сегодня я расскажу о splay-деревьях. Эти деревья не являются перманентно сбалансированными и на отдельных запросах могут работать даже линейное время. Однако, после каждого запроса они меняют свою структуру, что позволяет очень эффективно обрабатывать часто повторяющиеся запросы. Более того, амортизационная стоимость обработки одного запроса у них , что делает splay-деревья хорошей альтернативой для перманентно сбалансированных собратьев.

Splay-деревья

В середине восьмидесятых Роберт Тарьян и Даниель Слейтор предложили несколько красивых и эффективных структур данных. Все они имеют несложную базовую структуру и одну-две эвристики, которые их постоянно локально подправляют. Splay-дерево — одна из таких структур.

Splay-дерево — это самобалансирующееся бинарное дерево поиска. Дереву не нужно хранить никакой дополнительной информации, что делает его эффективным по памяти. После каждого обращения, даже поиска, splay-дерево меняет свою структуру.

Ниже я опишу алгоритм, как работает дерево на наборе попарно различных ключей, а потом приведу его анализ.

Алгоритм

Для описания структуры дерева нам пригодится простенький класс, описывающий отдельную вершину,

class Node:   def __init__(self, key, left = None, right = None, parent = None):     self.left   = left     self.right  = right     self.parent = parent     self.key    = key 

и две вспомогательные процедуры для работы с указателями на родителей.

def set_parent(child, parent):   if child != None:     child.parent = parent  def keep_parent(v):   set_parent(v.left, v)   set_parent(v.right, v) 

Основная эвристика splay-дерева — move-to-root. После обращения к любой вершине, она поднимается в корень. Подъем реализуется через повороты вершин. За один поворот, можно поменять местами родителя с ребенком, как показано на рисунке ниже.

def rotate(parent, child):   gparent = parent.parent   if gparent != None:     if gparent.left == parent:       gparent.left = child     else:       gparent.right = child    if parent.left == child:     parent.left, child.right = child.right, parent   else:     parent.right, child.left = child.left, parent    keep_parent(child)   keep_parent(parent)   child.parent = gparent 

Но просто поворачивать вершину, пока она не станет корнем, недостаточно. Хитрость splay-дерева в том, что при продвижении вершины вверх, расстояние до корня сокращается не только для поднимаемой вершины, но и для всех ее потомков в текущих поддеревьях. Для этого используется техника zig-zig и zig-zag поворотов.

Основная идея zig-zig и zig-zag поворотов, рассмотреть путь от дедушки к ребенку. Если путь идет только по левым детям или только по правым, то такая ситуация называется zig-zig. Как ее обрабатывать показано на рисунке ниже. Сначала повернуть родителя, потом ребенка.

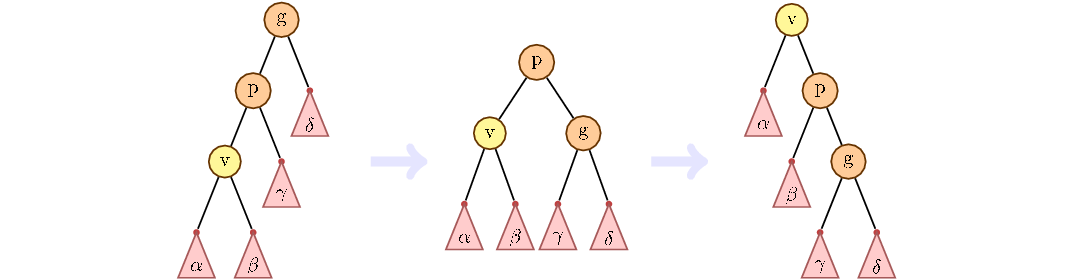
В противном случае, мы сначала меняем ребенка с текущим родителем, потом с новым.

Если у вершины дедушки нет, делаем обычный поворот:

Описанная выше процедура поднятия вершины с помощью zig-zig и zig-zag поворотов является ключевой для splay-дерева.

Примечание. В русском языке термин «splay» перевели как «расширять». Мне кажется, это не очень удачный перевод. Вы берете вершину и тянете ее наверх. В это время все другие вершины уходят вниз, поворачиваясь вокруг нее. Нечто похожее происходит, когда вы выворачиваете футболку. Так что слово «выворачивать» кажется здесь более подходящим.

def splay(v):   if v.parent == None:     return v   parent = v.parent   gparent = parent.parent   if gparent == None:     rotate(parent, v)      return v       else:     zigzig = (gparent.left == parent) == (parent.left == v)     if zigzig:       rotate(gparent, parent)       rotate(parent, v)     else:       rotate(parent, v)       rotate(gparent, v)     return splay(v) 

Процедура поиска в splay-дереве отличается от обычной только на последней стадии: после того, как вершина найдена, мы тянем ее вверх и делаем корнем через процедуру splay.

def find(v, key):   if v == None:     return None   if key == v.key:     return splay(v)   if key < v.key and v.left != None:     return find(v.left, key)   if key > v.key and v.right != None:     return find(v.right, key)   return splay(v) 

Чтобы реализовать вставку и удаление ключа, нам потребуются две процедуры: split и merge (разрезать и слить).

Процедура split получает на вход ключ key и делит дерево на два. В одном дереве все значения меньше ключа key, а в другом — больше. Реализуется она просто. Нужно через find найти ближайшую к ключу вершину, вытянуть ее вверх и потом отрезать либо левое, либо правое поддерево (либо оба).

def split(root, key):   if root == None:     return None, None   root = find(root, key)   if root.key == key:     set_parent(root.left, None)     set_parent(root.right, None)     return root.left, root.right   if root.key < key:     right, root.right = root.right, None     set_parent(right, None)     return root, right   else:     left, root.left = root.left, None     set_parent(left, None)     return left, root  

Чтобы вставить очередной ключ, достаточно вызвать split по нему, а затем сделать новую вершину-корень, у которой поддеревьями будет результат split-а.

def insert(root, key):   left, right = split(root, key)   root = Node(key, left, right)   keep_parent(root)   return root 

Процедура merge получает на вход два дерева: левое left и правое right. Для корректной работы, ключи дерева left должны быть меньше ключей дерева right. Здесь мы берем вершину с наименьшим ключом правого дерева right и тянем ее вверх. После этого в качестве левого поддерева присоединяем дерево left.

def merge(left, right):   if right == None:     return left   if left == None:     return right   right = find(right, left.key)   right.left, left.parent = left, right   return right 

Для того, чтобы удалить вершину, нужно поднять ее вверх, а потом слить ее левые и правые поддеревья.

def remove(root, key):   root = find(root, key)   set_parent(root.left, None)   set_parent(root.right, None)   return merge(root.left, root.right) 

Чтобы splay-дерево поддерживало повторяющиеся ключи, можно поступить двумя способами. Нужно либо каждому ключу сопоставить список, хранящий нужную доп. информацию, либо реализовать процедуру find так, чтобы она возвращала первую в порядке обхода LUR вершину с ключом, большим либо равным заданного.

Анализ

Заметим, что процедуры удаления, вставки, слияния и разделения деревьев работают за 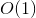+ время работы процедуры find.

Процедура find работает пропорционально глубине искомой вершины в дереве. По завершении поиска запускается процедура splay, которая тоже работает пропорционально глубине вершины. Таким образом, достаточно оценить время работы процедуры splay.

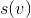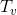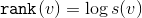Для анализа воспользуемся методом физика, про который я рассказывал в статье про амортизационный анализ. Пусть — размер поддерева с корнем в вершине . Рангом вершины назовем величину . Наш потенциал будет .

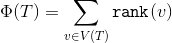Будем считать, что фактическое время процедуры splay(v) равно глубине 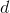вершины 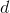. Отметим, что это также равно числу элементарных поворотов, которые будут выполнены в ходе процедуры.

Утверждение. Амортизационная стоимость операции splay от вершины в дереве 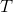с корнем составляет .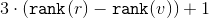

Доказательство.
Если — корень, то утверждение очевидно. В противном случае разделим процедуру splay(v) на этапы. В ходе каждого этапа выполняется один из трех поворотов: zig, zig-zig или zig-zag. На простой поворот уходит единица времени, на zig-zig и zig-zag — две единицы.

После каждого этапа ранг вершины будет меняться. Пусть изначально ранг составляет 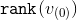, а после 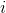-ого этапа — 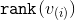. Для каждого этапа, кроме, быть может, последнего, мы покажем, что амортизационное время на его выполнение можно ограничить сверху величиной 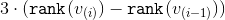. Для последнего этапа верхняя оценка составит 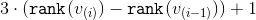. Просуммировав верхние оценки и сократив промежуточные значения рангов мы получим требуемое

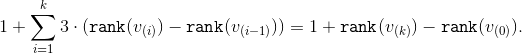
Нужно только заметить, что 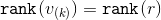, а .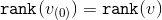

Теперь разберем каждый тип поворота отдельно.

Zig. Может выполняться только один раз, на последнем этапе. Фактическое время 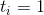. Посмотрим на рисунок и поймем, что ранги меняются только у вершин и .

Значит, амортизационная стоимость составит 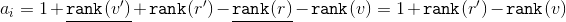. Ранги и сокращаются. Исходя из размеров соответствующих поддеревьев применим к формуле 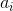неравенство:

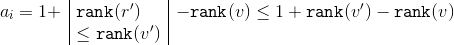
Значит, .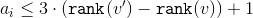

Zig-zig. Фактическое время 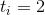. Заметим, что ранги меняются только у вершин , 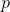и .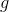

Тогда амортизационная стоимость 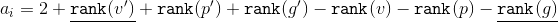. Ранги и 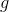можно сократить. Получим, что 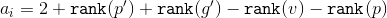. Исходя из размеров поддеревьев применим к формуле 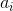два неравенства:

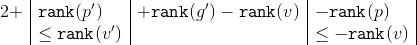
и получим, что .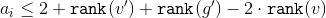

Наша цель — показать, что 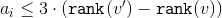. Для этого достаточно показать, что :

Для удобства перенесем ранги в левую часть и будем доказывать . По определению ранга . Последнее равенство разобъем на сумму . Посмотрим на рисунок и поймем, что .

Факт. 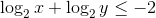для любых положительных 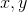таких, что .

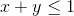Значит, . Получили требуемое.

Zig-zag.

Аналогично предыдущему случаю запишем амортизационную оценку: .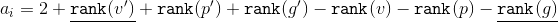

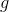Ранги и сокращаются. К формуле 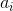применим следующие неравенства:

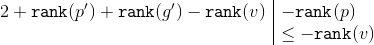
Значит, 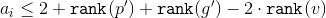. Это неравенство доказывается аналогично предыдущему случаю.

Таким образом мы разобрали все три случая и получили верхнюю оценку на амортизированное время через ранги.

Осталось заметить, что ранг любой вершины ограничен логарифмом размера дерева. Из чего следует следующая теорема.

Теорема. Операция splay амортизационно выполняется за .

Другие метрики и свойства

На десерт я хотел бы сослаться на википедию и представить здесь несколько интересных фактов про splay-деревья.

Теорема о статической оптимальности. Пусть 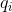— число раз, которое был запрошен элемент 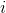. Тогда выполнение 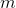запросов поиска на splay-дереве выполняется за .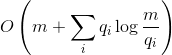

По сути этот факт сообщает следующее. Пусть мы заранее знаем, в каком количестве будут заданы запросы для различных элементов. Мы строим какое-то конкретное бинарное дерево, чтобы отвечать на эти запросы как можно быстрее. Утверждение сообщает, что с точностью до константы splay-дерево будет амортизационно работать не хуже, чем самое оптимальное фиксированное дерево, которое мы можем придумать.

Теорема о текущем множестве. Пусть 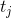— это число запросов, которое мы уже совершили с момента последнего запроса к элементу 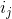; если еще не обращались, то просто число запросов с самого начала. Тогда время обработки 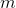запросов составит .

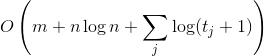Этот факт формализует мое рассуждение о кэше в начале статьи. По сути он говорит, что в среднем недавно запрошенный элемент не уплывает далеко от корня.

Сканирующая теорема Последовательный доступ (LUR) к элементам splay-дерева выполняется за .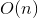

Этот факт имеет большое практическое следствие. Вместе с операциями split и merge, он делает splay-деревья отличной основой для структуры данных rope. Подробнее про нее можно прочитать постах Хабра Ropes — быстрые строки и Моноиды и их приложения….

Спасибо за внимание!

Литература

• Tarjan «Data Structures and Networks Algorithms»
• Sleator, Daniel D.; Tarjan, Robert E. (1985), «Self-Adjusting Binary Search Trees»