Предыстория

В свободное от работы время решил поразмыслить, а нельзя ли создать алгоритм соритировки который имел бы сложность O(n) не занимал бы много дополнительной памяти и мог бы быть легко распараллелен. И добился некоторого результата.

Представим, что у нас есть следующий набор чисел:

• 123
• 12345
• 22345
• 12345678
• 1

Как мы, будучи людьми будем сортировать этот массив данных? Правильно, будем выбирать самое, визуально длинное, число.
А если длина одинаковая, то будем сравнивать цифры в одном разряде. Я подумал, что можно точно также заставить работать компьютер.

Алгоритм

Итак, имеем на входе массив чисел размером N:

int[] array = new int[n]

Далее, каждый элемент массива представляем в двоичном виде и сохраняем в новом списке:

bool[][] bitMatrix = new bool[n][]; //битовая матрица нашего массива for (int i = 0; i < array.Length; i++) { 	BitArray bitArray = new BitArray (new int[1]{ array [i] }); 	bool[] bits = new bool[bitArray.Length]; 	bitArray.CopyTo (bits, 0); 	Array.Reverse (bits); 	bitMatrix [i] = bits; } 

Мы получили следующую матрицу:

Затем следует самая интересная часть: рекурсивная сортировка.
Для начала, давайте посмотрим на то, как бы мы сортировали эту битовую матрицу:

1. Смотрим на первую колонку
2. Выбираем все элементы где первый бит равен 1 в один список
3. Выбираем все элементы где первый бит равен 0 во второй список
4. Повторяем действия 2 и 3 для первого и второго списков, но уже для колонки номер два

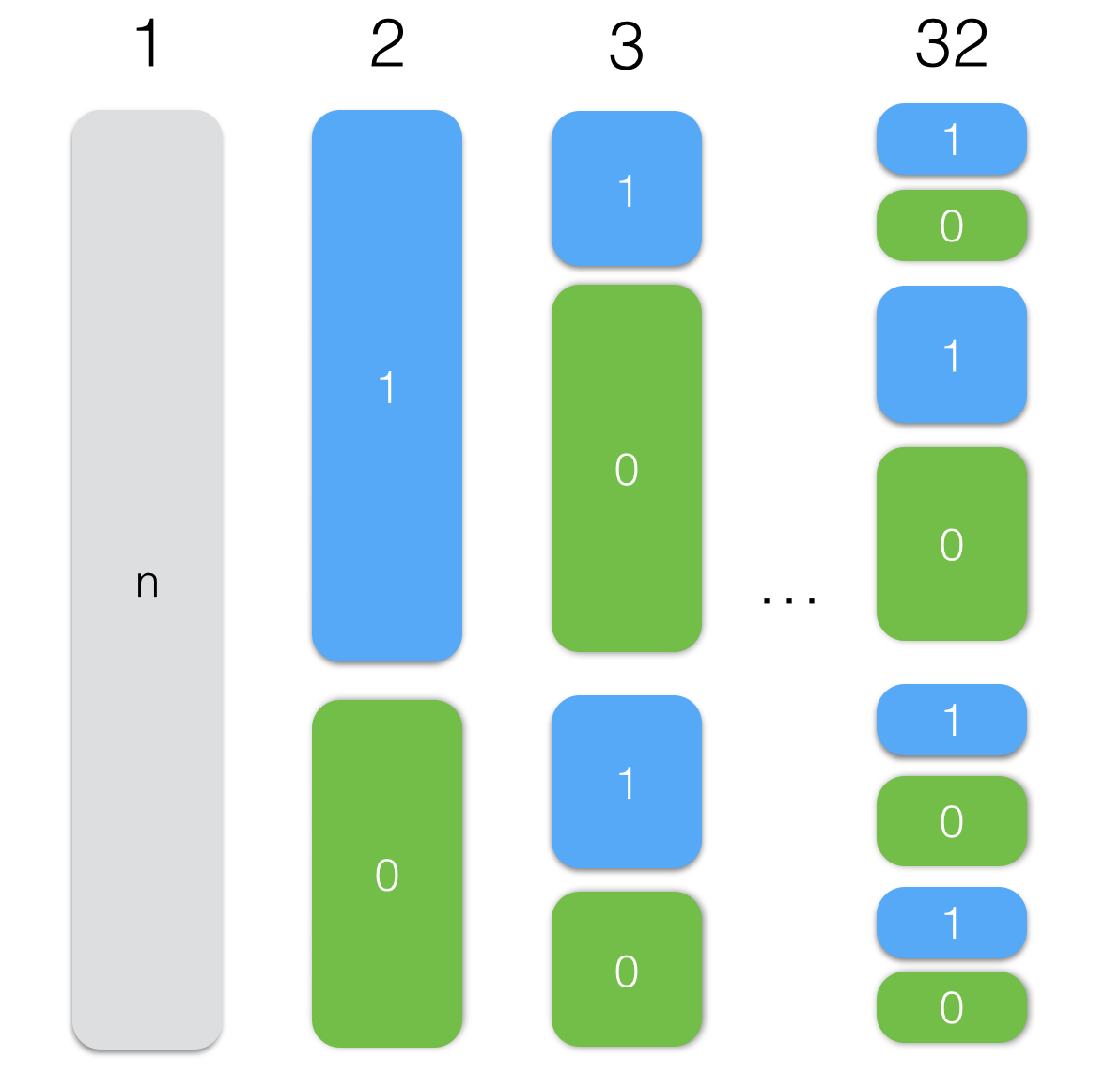
Код будет выглядеть следующим образом:

private void SortAlgorithm(bool[][] bitMatrix, int columnNumber) { 	List<bool[]> ones = new List<bool[]> (); 	List<bool[]> zeros = new List<bool[]> ();  	for (int i = 0; i < bitMatrix.Length; i++) 	{ 		if (bitMatrix[i][columnNumber]) 			ones.Add(bitMatrix[i]); 		else 			zeros.Add(bitMatrix[i]); 	}  	columnNumber++;  	if (columnNumber == MAX_COLUMN_COUNT)//MAX_COLUMN_COUNT = sizeof(int)*8 	{ 		sortedBitMatrix.AddRange(ones); 		sortedBitMatrix.AddRange(zeros); 		return; 	}  	if (ones.Count != 0) 		SortAlgorithm (ones.ToArray(), columnNumber); 	if (zeros.Count != 0) 		SortAlgorithm (zeros.ToArray(), columnNumber); } 

sortedBitMatrix используется для хранения отсортированной битовой матрицы.
Для преобразования битовой матрицы обратно в массив воспользуемся следующим методом:

private int[] ConvertBitMatrixToArray(List<bool[]> bitMatrix) { 	int[] resultArray = new int[bitMatrix.Count]; 	int count = 0; 	for (int i = 0; i < bitMatrix.Count; i++) 	{ 		bool[] bits = bitMatrix [i]; 		Array.Reverse(bits); 		BitArray bitArray = new BitArray(bits); 		int[] tmpArray = new int[1]; 		bitArray.CopyTo(tmpArray, 0); 		resultArray [count] = tmpArray [0]; 		count++; 	} 	return resultArray; }

Результатом метода будет отсортированный массив.

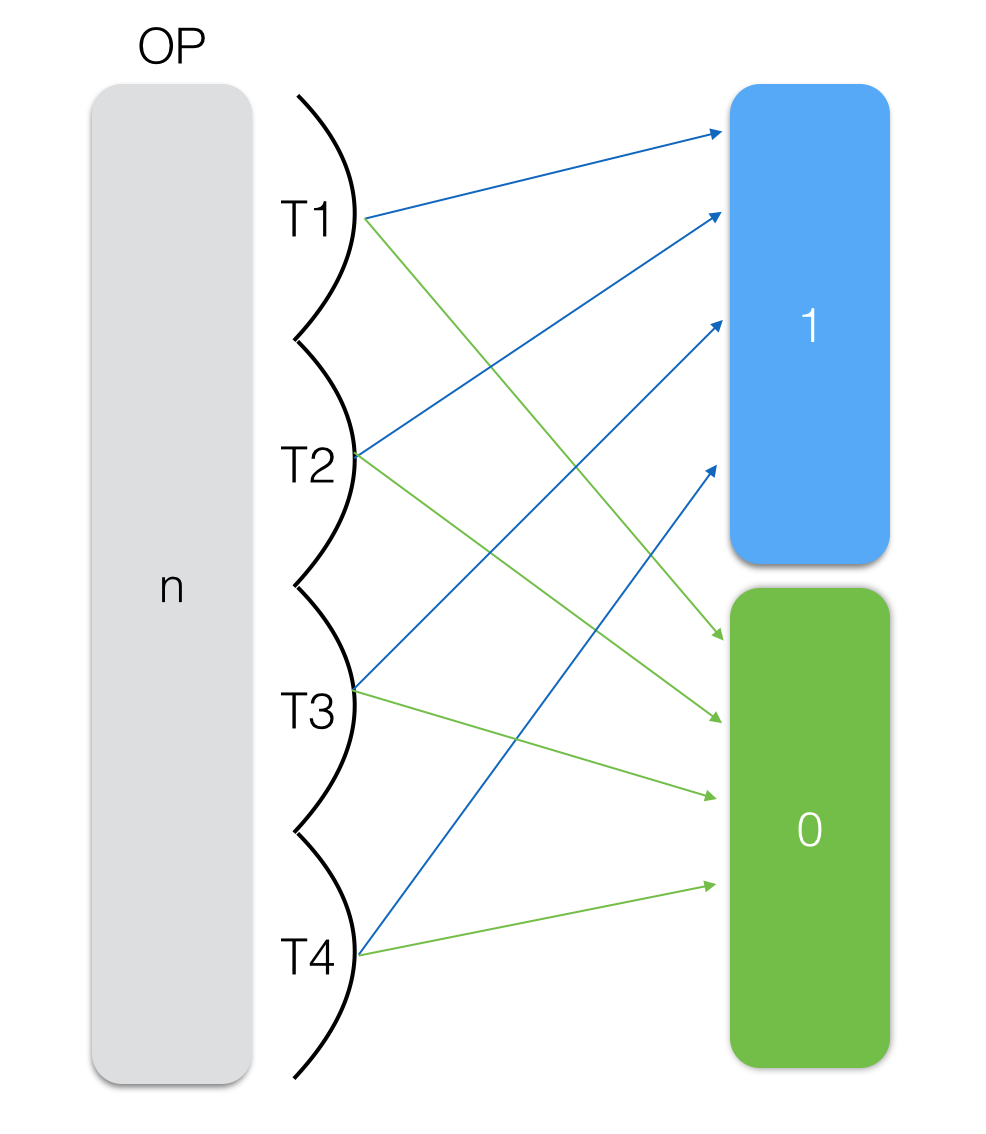
А как же распараллеливание?

Так как основная часть времени тратится на прохождение по каждой колонке битовой матрицы в поиске единиц и нулей, то этот процесс можно запустить в нескольких потоках.
Каждый поток будет искать единицы и нули в части матрицы:

Сложность

Для сортировки заданного массива нам нужны следующие итерации:

1. Создание битовой матрицы: n
2. Поиск нулей и единиц: 32n
3. Преобразование отсортированной битовой матрицы: n

Итого: 34n, что является O(n)

Интересно Ваше мнение.
Спасибо за внимание.

P.S. github.com/koljaka/BitSorting