Динамические деревья (link/cut trees) мало освещены в русскоязычном интернете. Я нашел только краткое описание на алголисте. Тем не менее эта структура данных очень интересна. Она находится на стыке двух областей: потоки и динамические графы. 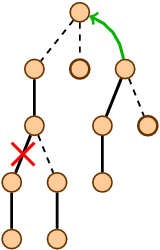
В первом случае динамические деревья позволяют построить эффективные алгоритмы для задачи о поиске максимального потока. Улучшенные алгоритмы Диница и проталкивания предпотока работают за 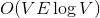 и
и 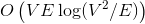 соответственно. Если вы не знаете, что такое поток, и на лекциях у вас такого не было, спешите пополнить свои знания в Кормене.
соответственно. Если вы не знаете, что такое поток, и на лекциях у вас такого не было, спешите пополнить свои знания в Кормене.
Второй случай требует небольшого введения. Динамические графы — это активно развивающаяся современная область алгоритмов. Представьте, что у вас есть граф. В нем периодически происходят изменения: появляются и исчезают ребра, меняются их веса. Изменения нужно быстро обрабатывать, а еще уметь эффективно считать разные метрики, проверять связность, искать диаметр. Динамические деревья являются инструментом, который позволяет ловко манипулировать с частным случаем графов, деревьями.
Перед тем, как нырнуть под кат, попробуйте решить следующую задачу. Дан взвешенный граф в виде последовательности ребер. По последовательности можно пройти только один раз. Требуется посчитать минимальное покрывающее дерево, используя 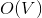 памяти и
памяти и 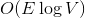 времени. По прочтении статьи вы поймете, как легко и просто можно решить эту задачу, используя динамические деревья.
времени. По прочтении статьи вы поймете, как легко и просто можно решить эту задачу, используя динамические деревья.
Постановка задачи
Динамические деревья имеют много разных модификаций, заточенных под конкретные задачи. Мы сейчас изучим базовую версию, а потом будем допиливать ее по требованию.
Представим, что у нас есть набор деревьев вкупе из 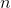 вершин. Каждое дерево подвешано за корень. Нам приходит следущий набор запросов.
вершин. Каждое дерево подвешано за корень. Нам приходит следущий набор запросов.
-
make_tree(v)— создать новое дерево с вершинойv -
link(u, v)— подвесить дерево с корнем в вершинеuк вершинеv. -
cut(u, v)— разрезать ребро (u,v). -
find_root(v)— найти корень дерева, в котором лежит вершинаv. -
depth(v)— найти глубину вершиныv.
Хочется обрабатывать все запросы за близкое к  время.
время.
Заметим, что, не будь запросов cut и depth, система непересекающихся множеств (5, 6, 7) могла бы решить эту задачу.
Динамические деревья использует внутри себя деревья поиска. Интересная особенность, что с произвольными сбалансированными деревьями они обрабатывают все вышеописанные запросы амортизационно за  . На splay-деревьях эти же запросы обрабатываются амортизационно за
. На splay-деревьях эти же запросы обрабатываются амортизационно за  . Памяти используется
. Памяти используется 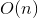 .
.
Внутреннее представление
Высокая скорость достигается за счет хитрого внутреннего представления. Разобьем каждое дерево на набор путей. Каждая вершина будет лежать ровно на одном пути, и никакие два пути не будут пересекаться. Каждый путь должен соединять потомка с предком.

Для работы с путями воспользуемся деревьями поиска по неявному ключу. Чтобы не было путаницы в терминологии, давайте называть деревья, которые мы разбиваем на пути, представляемыми, а деревья, в которые мы эти пути складываем, опорными.
Порядок элементов в опорном дереве направим так, что если выписать все его узлы в порядке обхода левое поддерево-ключ-правое поддерево, то заданная последовательность будет соответствовать прохождению хранимого пути в представляемом дереве от верхней вершины к нижней.
Отметим, что ребра, которые не участвуют в разбиении, всегда соединяют верхнюю вершину пути с ее родителем. В каждой вершине будем хранить ссылку. Если вершина лежит на верху пути, ссылка указывает на ее родителя. В корне дерева ссылка указывает на None.
Деревья поиска по неявному ключу
Здесь я только кратко изложу идею, а все подробностями смотрите в посте про декартовы деревья.
Деревья поиска по неявному ключу похожи на обычные деревья, только ключ в них не используется. Искать в них можно 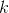 -ый по порядку элемент. Для этого в каждом узле записывается размер его поддерева. В зависимости от размеров левого и правого поддеревьев мы выбираем куда идти. Выглядит это как-то так:
-ый по порядку элемент. Для этого в каждом узле записывается размер его поддерева. В зависимости от размеров левого и правого поддеревьев мы выбираем куда идти. Выглядит это как-то так:
def find(v, k): if v == None: return None threshold = size(v.left) if k == threshold: return v if k < threshold and v.left != None: return find(v.left, k) if k > threshold and v.right != None: return find(v.right, k - threshold - 1) return None При балансировке порядок элементов в деревьях поиска не меняется. Поэтому деревья можно рассматривать как умные массивы. Вы можете найти 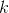 -ый элемент, удалить его или вставить на нужную позицию. Все операции выполнимы за
-ый элемент, удалить его или вставить на нужную позицию. Все операции выполнимы за  .
.
Если говорить о декартовых или splay-деревьях, то у нас появляется две дополнительных возможности: разрезать и сливать деревья. Благодаря этому мы можем сливать и разрезать последовательности элементов за  .
.
Применительно к нашей задаче деревья поиска по неявному ключу позволяют нам разрезать один путь на два, сливать два в один и обращаться к 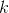 -ому по счету элементу за
-ому по счету элементу за  .
.
Expose и его друзья
Ключевая процедура в динамических деревьях — expose(v). Процедура перестраивает пути в представляемом дереве. Мы будем поддерживать инвариант, что после того, как была запрошена вершина v, она будет лежать в одном пути с корнем. При этом v окажется конечной вершиной пути.

Если вы написали expose, то все остальное выглядит более менее очевидно.
def link(u, v): u.link = v expose(u) Ставим ссылку на родителя и запускаем expose, чтобы поддержать инвариант.
def cut(u, v): expose(v) u.link = None expose(u) Первым вызовом expose мы помещаем вершины u и v в разные пути. Смело обнуляем ссылку, и запускаем второй expose для поддержания инварианта.
def find_root(v): expose(v) return leftest(supportRoot(v)) После вызова expose вершина v и корень будут лежать в одном опорном дереве. Если дерево сбалансировано, достаточно подняться до корня, а потом спуститься до крайне левого узла. Это будет корень. Я условно обозначил подъем до корня через supportRoot, а спуск до крайне левого элемента через leftest. В случае splay-дерева, supportRoot заменяется на splay.
def depth(v): expose(v) return size(supportRoot(v)) - 1 Снова делаем expose, снова вершина v и корень на одном пути. Размер опорного дерева равен числу узлов в этом пути. Поднимаемся до корня, находим размер опорного дерева. Вычитаем единицу, чтобы получить число ребер.
Давайте еще найдем наиближайшего общего предка (lowest common ancestor).
def lca(u, v): expose(u) expose(v) return leftest(supportRoot(u)).link Нарисуйте на бумажке, что произойдет, и поймите, что это действительно lca. Кстати, вы заметили, что если вершины лежат в разных деревьях, то процедура вернет None? Не правда ли, очень мило с ее стороны?
Сама процедура expose сводится к следующему: находим корень опорного дерева, в котором лежит текущий узел; прыгаем до левейшего элемента, чтобы попасть на верх пути. Эти операции выполнимы за  . Пройдем по ссылке на следующее опорное дерево и сольем его с предыдущим. Так будем делать, пока не достигнем корня представляемого дерева.
. Пройдем по ссылке на следующее опорное дерево и сольем его с предыдущим. Так будем делать, пока не достигнем корня представляемого дерева.
Мы будем использовать вспомогательную процедуру cutout, которая отрезает путь на вершине v и проставляет нужные ссылки детям.
def expose(v): cutout(v) v = leftest(supportRoot(v)) while v.link != None: cutout(v.link) merge(supportRoot(v.link), (v - v.link), supportRoot(v)) v.link = None v = leftest(supportRoot(v)) return v
Некорневые деревья
Динамические деревья можно расширить до некорневых. Достаточно уметь переподвешивать деревья. Посмотрим на следующую процедуру:
def revert(v): expose(v) reverse(supportRoot(v)) Процедура revert(v) соединяет вершину v с текущим корнем. Заметим, что если бы корнем была вершина v, то поменялся бы только порядок элементов на пути между v и корнем. Поскольку пути хранятся в деревьях по неявному ключу, мы можем реализовать разворот через отложенные операции на отрезках (еще раз 4).
Добавление и удаление ребер реализуется тривиально.
def link_edge(u, v): revert(u) link(u, v)
def cut_edge(u, v): revert(v) cut(u, v) В первом случае revert обеспечивает, что u будет корнем поддерева. Во-втором — вершина v будет родителем u.
Можно также найти расстояние между вершинами из одного дерева.
def dist(u, v): revert(v) return depth(u) Операции на отрезках дают большие возможности. Например, алгоритмы поиска максимального потока используют их, чтобы быстро найти пропускную способность в остаточной сети, а также проталкивать поток вдоль всего пути сразу. Подробнее можно посмотреть в книжке Тарьяна «Data Structures and Network Algorithms».
Касательно задачи во вступлении. Основная проблема, что делать, если при добавлении очередного ребра появляется цикл. Нужно быстро искать самое тяжелое ребро на пути между заданными вершинами u и v. revert от u, expose от v, и мы получили опорное дерево, содержащее этот путь. Деревья по неявному ключу позволяют быстро искать максимум. Поэтому обнаружить ребро не составит труда.
Техническая особенность: если в опорном дереве в каждой вершине хранится вес ребра идущего к родителю, то при изменении корня родители меняются. Проблему можно решить, если хранить веса ребер к следующей и предыдущей вершинам вдоль пути. Альтернативное решение — завести для каждого ребра отдельную вершину и только там хранить веса.
Анализ
Пусть  . Время работы всех вышеописанных процедур состоит из одного-двух запусков процедуры
. Время работы всех вышеописанных процедур состоит из одного-двух запусков процедуры expose и константного
числа операций над опорными деревьями. Операции над опорными деревьями выполняются за  .
.
Оценим процедуру expose. Пусть она состоит из 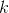 слияний и разрезов опорных деревьев. Это число выражается количеством ребер, которые мы добавим в строящийся путь. Посчитаем их суммарное число, чтобы получить амортизационную оценку.
слияний и разрезов опорных деревьев. Это число выражается количеством ребер, которые мы добавим в строящийся путь. Посчитаем их суммарное число, чтобы получить амортизационную оценку.
Каждой вершине назначим вес, равный размеру поддерева, корнем которого она является. Ребро идущее от родителя к ребенку назовем тяжелым, если вес ребенка строго больше половины веса родителя. Остальные ребра назовем легкими.
Утверждение. Число легких ребер на пути от корня до любого листа не превосходит 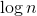 .
.
Каждый раз, спускаясь от родителя к ребенку по легкому ребру, размер текущего поддерева уменьшается хотя бы в два раза. Поскольку размер дерева не превышает 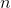 , то число легких ребер на пути от корня до любого листа не превосходит
, то число легких ребер на пути от корня до любого листа не превосходит 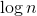 .
. 
Исходя из предыдущего утверждения, за все вызовы expose мы добавим в путь 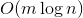 легких ребер. Посчитаем число тяжелых ребер, которые мы добавим. При добавлении каждого тяжелого ребра будем класть на него монетку. Когда ребро перестает лежать на пути, эту монетку заберем. Оценим, сколько монеток мы потратим.
легких ребер. Посчитаем число тяжелых ребер, которые мы добавим. При добавлении каждого тяжелого ребра будем класть на него монетку. Когда ребро перестает лежать на пути, эту монетку заберем. Оценим, сколько монеток мы потратим.
Мы можем забрать монетку только в двух случаях: а) от родителя был вызван expose и нас отрезали, б) теперь на пути лежит соседнее ребро. Первый случай может произойти не более 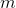 раз. Во втором случае соседнее выбранное ребро будет легким. Такое может произойти не более
раз. Во втором случае соседнее выбранное ребро будет легким. Такое может произойти не более  раз. По окончании работы в дереве может остаться не более
раз. По окончании работы в дереве может остаться не более  тяжелого ребра. Значит, всего тяжелых ребер не больше
тяжелого ребра. Значит, всего тяжелых ребер не больше  . Таким образом, суммарное время обработки всех операций
. Таким образом, суммарное время обработки всех операций  .
.
Практические испытания
На практике для деревьев с маленьким диаметром лучше использовать обычный DFS. Динамические деревья становятся заметно эффективными, когда мы работаем с большими деревьями и большим количеством запросов link и cut. Наиболее высокую производительность показывает реализация на splay-деревьях. Подробнее можно узнать в обзоре Тарьяна, Вернека «Dynamic Trees in Practice».
Реализацию на питоне можно найти здесь.
О жизни…
Если вы дочитали до этого места, то я вас поздравляю. Я хотел бы передать послание двум категориям своих читателей.
Первые — это студенты-программисты третьих-четвертых курсов бакалавриата. Возможно, ничего подобного вам не рассказывали на лекциях, и вам хотелось бы восполнить пробелы по алгоритмам и многим другим темам. У вас есть возможность поступить в магистратуру Академического Университета на разработку программного обеспечения. Это отличный шанс пополнить свои знания, поставить руку под надзором опытных программистов, а для иногородних — переехать в Питер. Учиться здесь не просто, но оно того стоит.
Вторые — это люди, кочующие между Project Euler и Braingames, между Braingames и Topcoder. Вы ищите математических задач? Теоретическая информатика велика, и для вас обязательно найдется место и задача. Посмотрите книги про приближенные (8, 9), экспоненциальные (10), параметризованные (11) алгоритмы, коммуникационную сложность (12), структурную сложность (13). Если вам это интересно, приходите учиться на теоретическую информатику.
Не упустите свою возможность!
Литература
ссылка на оригинал статьи http://habrahabr.ru/company/spbau/blog/216733/
Добавить комментарий