Для тех, кому это тоже интересно — эта статья. Те, кто хорошо знаком с OpenFOAM или с методами в нём реализованными — пишите о найденных ошибках, если таковые имеются — лучше в личку.
В данной статье я на простом примере-задаче опишу операции, которые происходят в ходе расчёта в OpenFOAM.
Итак, дана геометрия — куб со стороной 1 метр:
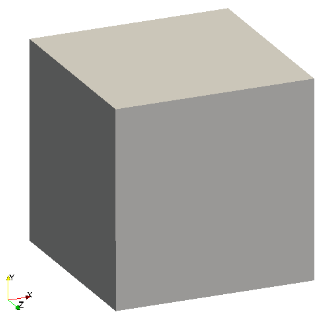
Граничные условия следующие: вход, выход, остальные грани — гладкие стенки.

Построение сетки — делим куб на 5 равных частей вдоль оси Z.

Поведение потока задаётся уравнением переноса (1).
(1)
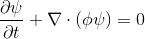 ,
,
где 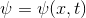 выражает концентрацию некоторого вещества, а
выражает концентрацию некоторого вещества, а  выражает перенос вещества, поток.
выражает перенос вещества, поток.
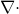 .
.Напомню, что существует оператор набла (оператор Гамильтона), который записывается следующим образом:
 ,
,
где i, j, k — единичные векторы.
Если скалярно умножить оператор набла на векторную величину, то мы получим дивергенцию данного вектора:
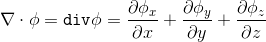
«С точки зрения физики, дивергенция векторного поля является показателем того, в какой степени данная точка пространства является источником или стоком этого поля»
Если умножить оператор набла на скаляр, получается градиент этого скаляра:
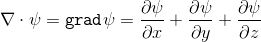
Градиент показывает увеличение или уменьшение по какому-либо направлению величины скаляра  .
.
Разбиение по пространству
Метод конечных объёмов предусматривает, что (1) в интегральной форме (2) будет выполняться для каждого конечного объёма 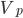 .
.
(2)
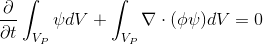 ,
,
где 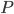 — центр конечного объёма.
— центр конечного объёма.

Упростим, преобразуем первое слагаемое выражения (2) следующим образом:
(2.1) (HJ-3.12)*

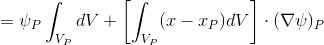
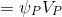
Как видно — мы приняли, что значение величины  в некоторой точке
в некоторой точке  внутри конечного объёма можно вычислить как:
внутри конечного объёма можно вычислить как:
 ,
,
где 
Для упрощения второго слагаемого выражения (2) вспомним обобщённую теорему Гаусса-Остроградского: интеграл от дивергенции векторного поля  по объёму
по объёму 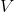 , равен потоку вектора через поверхность
, равен потоку вектора через поверхность 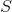 , ограничивающую данный объём:
, ограничивающую данный объём:
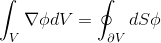 ,
,
где  замкнутая поверхность, ограничивающая объём
замкнутая поверхность, ограничивающая объём 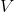 ,
,
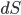 — вектор, по величине равный площади бесконечномалого участка на грани, направлен вектор по нормали от объёма
— вектор, по величине равный площади бесконечномалого участка на грани, направлен вектор по нормали от объёма  .
.

Учитывая то, что конечный объём ограничен набором плоских граней, можно выражение (2.3) преобразовать к сумме интегралов по поверхности:
(2.4) (HJ-3.13)
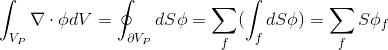 ,
,
где  выражает значение переменной в центре грани,
выражает значение переменной в центре грани,
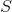 — вектор площади, выходит из центра грани, направлен от центра ячейки.
— вектор площади, выходит из центра грани, направлен от центра ячейки.
Вектор площади 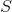 указывает от центра
указывает от центра 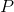 , если мы его рассматриваем относительно нашей ячейки (в OpenFOAM такое отношение между ячейкой и вектором
, если мы его рассматриваем относительно нашей ячейки (в OpenFOAM такое отношение между ячейкой и вектором 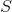 , а точнее между ячейкой и гранью, обозначается owner). Для соседних ячеек этот вектор
, а точнее между ячейкой и гранью, обозначается owner). Для соседних ячеек этот вектор 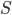 указывает внутрь (отношение neighbour). Направление влияет на знак величины и это важно при суммировании.
указывает внутрь (отношение neighbour). Направление влияет на знак величины и это важно при суммировании.

(HJ-3.16)
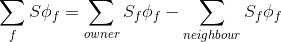
Численно  это площадь одной грани. А вот значение
это площадь одной грани. А вот значение  выражается через значения
выражается через значения  в других ячейках — способ такого выражения носит название разностной схемы. В нашей задаче в файле fvSchemes тип разностной схемы задан следующим образом:
в других ячейках — способ такого выражения носит название разностной схемы. В нашей задаче в файле fvSchemes тип разностной схемы задан следующим образом:
divSchemes { default none; div(phi,psi) Gauss linear; } Gauss — означает, что выбрана центральная разностная схема;
linear — означает, что интерполяция с центров ячеек на центры поверхностей будет происходить линейно.

Значение в центре грани будет вычисляться по следующей схеме:
(HJ-3.19)
 ,
,

Учитывая (2.1) и (2.4) выражение (2) принимает вид:
(3)
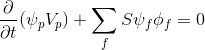
Дискретизация по времени
Согласно методу конечных объёмов проводится дискретизация по времени и выражение (3) записывается как:
(4)
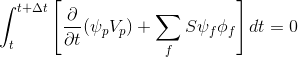
Проинтегрируем (4):
(4.1)
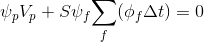
Разделим левую и правую часть на  :
:
(5)
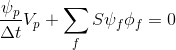
Формирование матрицы дискретизации
Теперь мы можем получить систему линейных уравнений для каждого конечного объёма 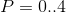 .
.
Для P = 0 выражение (5) примет вид:


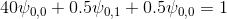
Для P=1:


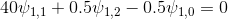
Для P=4:


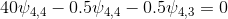
Так как на выходе задано граничное условие
outlet { type zeroGradient; } то получаем

Система линейных алгебраических уравнений (СЛАУ) может быть представлена в матричном виде как
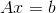 ,
,
где
=== A(i,j) === 40.5 0.5 0 0 0 -0.5 40 0.5 0 0 0 -0.5 40 0.5 0 0 0 -0.5 40 0.5 0 0 0 -0.5 40.5 === b(i,j) === 1 0 0 0 0 Далее полученная СЛАУ решается решателем, указанным в fvSchemes.
И в итоге получается вектор значений 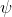
psi = dimensions [0 0 0 0 0 0 0]; internalField nonuniform List<scalar> 5(0.0246875 0.000308546 3.85622e-06 4.81954e-08 5.95005e-10); на основе которого получаются значения для вектора 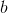
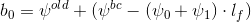
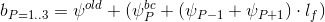

Затем вектор 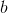 подставляется в СЛАУ
подставляется в СЛАУ 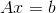 и происходит новая итерация расчёта вектора
и происходит новая итерация расчёта вектора 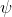 .
.
И так до тех пор, пока невязка не достигнет требуемых пределов.
Ссылки
* Некоторые уравнения в этой статье взяты из диссертации Ясака Хрвое (HJ — номер уравнения) и если кому-то захочется прочитать про них подробнее (http://powerlab.fsb.hr/ped/kturbo/OpenFOAM/docs/HrvojeJasakPhD.pdf)
Скачать файлы задачи можно здесь:
github.com/j-avdeev/case
Файлы решателя:
github.com/j-avdeev/matrHyper1Foam
В качестве бонуса — видео, как распространяется концентрация 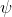 .
.
ссылка на оригинал статьи http://habrahabr.ru/post/218483/
Добавить комментарий