
В чём задача
Прежде всего я напомню, о чём мы вообще говорим. Один из основных инструментов машинного обучения — это теорема Байеса:
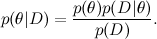
Здесь D — это данные, θ — параметры модели, которые мы хотим обучить, а 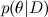 — это распределение θ при условии имеющихся данных D; про теорему Байеса мы уже подробно говорили одной из предыдущих статей. В машинном обучении мы, как правило, хотим найти апостериорное распределение
— это распределение θ при условии имеющихся данных D; про теорему Байеса мы уже подробно говорили одной из предыдущих статей. В машинном обучении мы, как правило, хотим найти апостериорное распределение 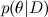 , а затем предсказать новые значения переменных
, а затем предсказать новые значения переменных 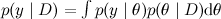 . В сложных графических моделях всё это, как мы обсуждали в предыдущих сериях, обычно сводится к тому, что у нас есть большое и запутанное распределение разнообразных случайных величин
. В сложных графических моделях всё это, как мы обсуждали в предыдущих сериях, обычно сводится к тому, что у нас есть большое и запутанное распределение разнообразных случайных величин 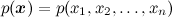 , которое раскладывается в произведение распределений попроще, и наша задача — провести маргинализацию, т.е. суммировать по части переменных или найти ожидание функции от части переменных. Заметим, что все наши задачи так или иначе сводятся к тому, чтобы подсчитать математическое ожидание разных функций при условии сложного распределения, обычно условного распределения модели, в которую подставлены значения некоторых переменных. Также можно считать, что мы умеем считать значение совместного распределения в любой его точке — это обычно несложно следует из общего вида модели, а сложность как раз в том, чтобы по куче этих переменных просуммировать-проинтегрировать.
, которое раскладывается в произведение распределений попроще, и наша задача — провести маргинализацию, т.е. суммировать по части переменных или найти ожидание функции от части переменных. Заметим, что все наши задачи так или иначе сводятся к тому, чтобы подсчитать математическое ожидание разных функций при условии сложного распределения, обычно условного распределения модели, в которую подставлены значения некоторых переменных. Также можно считать, что мы умеем считать значение совместного распределения в любой его точке — это обычно несложно следует из общего вида модели, а сложность как раз в том, чтобы по куче этих переменных просуммировать-проинтегрировать.
Мы уже знаем, что точный вывод вести сложно, и эффективные алгоритмы получаются только для случая фактор-графа без циклов или с маленькими циклами. Однако реальные модели часто содержат кучу переменных, которые связаны друг с другом достаточно плотно и образуют массу циклов. Мы немного говорили о вариационных приближениях — одном возможном способе преодолеть возникающие трудности. А сегодня я расскажу о другом, ещё более популярном методе — о сэмплировании.
Приближение Монте-Карло
Идея проста до чрезвычайности. Мы уже выяснили, что в принципе всё, что нам нужно, выражается в виде ожиданий разнообразных функций по нашему сложному и запутанному распределению p(x). Как подсчитать ожидание функции по распределению? Если мы умеем сэмплировать из этого распределения, т.е. брать случайные точки 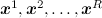 по распределению p(x), то ожидание любой функции можно приблизить как среднее арифметическое в сэмплированных точках:
по распределению p(x), то ожидание любой функции можно приблизить как среднее арифметическое в сэмплированных точках:
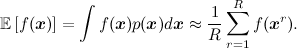
Например, чтобы посчитать среднее (матожидание), нужно усреднить по сэмплам x.
Таким образом, вся наша задача фактически сводится к тому, чтобы научиться сэмплировать точки по распределению при условии, что мы можем в любой точке считать значение этого распределения.
В чём тут сложность
Человеку, воспитанному на функциях от одной переменной (т.е. фактически любому человеку, прослушавшему базовый курс матанализа в вузе), может показаться, что большой проблемы тут нет, и все эти разговоры ни о чём — известно же, как приближённо посчитать интеграл, надо просто разбить отрезок на части, посчитать функцию в середине каждого маленького отрезочка, прямоугольники там, трапеции, ну вы понимаете… И действительно, в сэмплировании из распределений от одной переменной нет ничего сложного. Сложности, как всегда, начинаются с ростом размерности — если в размерности 1 нужно посчитать 10 значений функции, чтобы разбить интервал на отрезки со стороной 0.1, то в размерности 100 таких значений нужно будет уже 10100, что гораздо печальнее. Этот и другие эффекты, которые делают работу в высокой размерности совершенно непохожей на привычную нам размерность 2-3, получили название «проклятие размерности» (curse of dimensionality); там есть и другие интересные контринтуитивные эффекты, возможно, стоит когда-нибудь поговорить об этом подробнее.
Есть и ещё одна сложность — выше я писал, что мы можем считать значение распределения в любой точке. На самом же деле обычно мы можем считать не значение распределения p(x), а значение некоторой функции p*(x), которая пропорциональна p(x). Вспомните теорему Байеса — из неё мы получаем не само апостериорное распределение, а пропорциональную ему функцию:
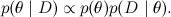
Обычно на этом месте мы говорили, что этого достаточно, а точное значение вероятности можно просто подсчитать, нормализовав полученное распределение так, чтобы оно суммировалось в единицу (т.е. вычислив знаменатель в теореме Байеса). Однако это как раз и есть та сложная задача, которую мы сейчас пытаемся научиться решать: просуммировать все значения сложного распределения. Поэтому в реальной жизни мы не можем рассчитывать на значение истинных вероятностей, только на некоторую пропорциональную им функцию p*.
Что же делать: сэмплируем под графиком
Несмотря на все вышеперечисленные сложности, сэмплирование делать всё-таки возможно, и это действительно один из главных приёмов приближённого вывода. Более того, как мы скоро увидим, делать сэмплирование совсем не так сложно, как кажется. В этом разделе я расскажу об основной идее, на которой так или иначе основаны все алгоритмы сэмплирования. Идея такая: если равномерно выбрать точку под графиком функции плотности распределения p, то её X-координата будет взята как раз по распределению p. Это очень легко понять интуитивно: представьте себе график плотности и разбейте его на маленькие столбики, примерно так (графики сделаны в matplotlib):
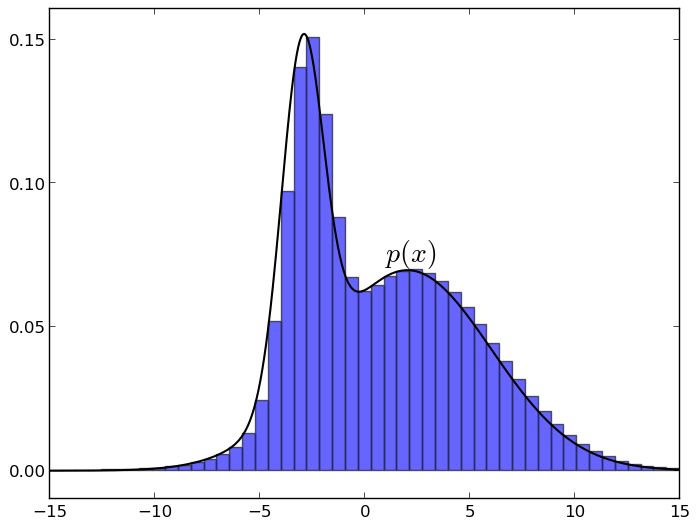
Теперь видно, что когда вы берёте случайную точку под графиком, каждая X-координата будет встречаться с вероятностью, пропорциональной высоте своего столбика, т.е. как раз со значением функции плотности на этом столбике.
Таким образом, нам нужно только научиться брать случайную точку под графиком плотности нужного распределения. Как же это сделать?
Первая идея, которая реально работает и часто применяется на практике — так называемая выборка с отклонением (rejection sampling). Давайте предположим, что у нас есть некое другое распределение q (точнее, пропорциональная ему функция q*), которое мы уже умеем сэмплировать. Обычно это какое-нибудь классическое распределение — равномерное или нормальное. Здесь стоит отметить, что сэмплировать из нормального распределения — это тоже не вполне тривиальная задача, но мы сейчас её пропустим, для нас сейчас достаточно знать, что «люди так делать умеют». Далее, предположим, что мы знаем про него такую константу c, что для всех x 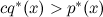 . Тогда мы сумеем сэмплировать p таким образом:
. Тогда мы сумеем сэмплировать p таким образом:
- берём сэмпл x по распределению q*(x);
- берём случайное число u равномерно из интервала
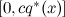 ;
; - вычисляем p*(x); если оно больше u, то x добавляется в сэмплы, а если меньше (т.е. если u не попало под график плотности p*), то x отклоняется (отсюда и выборка с отклонением).
Вот картинка, иллюстрирующая выборку с отклонением (нормальное распределение, подобранное так, чтобы мажорировать смесь двух других гауссианов):
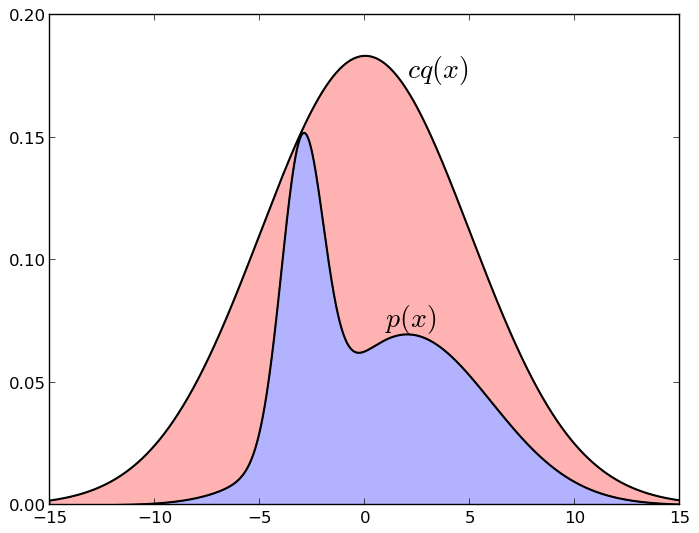
Если точка под графиком cq* попадает под график p*, т.е. в синюю зону, мы её берём; а если над ним, т.е. в красную зону, — не берём. Опять же, легко интуитивно понять, почему это работает: мы берём случайную точку равномерно под графиком cq*, а потом оставляем только те точки, которые при этом попали под график p* — понятно, что при этом у нас останется как раз равномерное распределение под графиком p*. Столь же понятно, что если нам удастся выбрать q достаточно похожим на p (например, мы знаем примерно, где сосредоточено p, и накрываем эту область гауссианом), то этот метод будет гораздо эффективнее, чем просто разбивать всё пространство на одинаковые кусочки. Но для того, чтобы метод работал, нужно, чтобы cq действительно достаточно хорошо приближало p — если площадь синей зоны составляет 10-10 от площади красной, никаких сэмплов не получится…
Есть разные варианты этой идеи, на которых я не буду останавливаться подробно. Если вкратце, то эта идея и её вариации хорошо работают со сложными плотностями в размерности, исчисляемой единицами, но в действительно высокой размерности всё-таки начинаются сложности. Из-за эффектов проклятия размерности классические пробные распределения q получают разные неприятные свойства (например, в высокой размерности кожура апельсина занимает почти весь его объём, и, в частности, нормальное распределение тоже почти целиком сосредоточено в очень тонкой <<кожуре>>, а вовсе не около нуля), сэмплы в нужных местах не удаётся получить, и всё дело часто проваливается. Нужны другие методы.
Алгоритм Метрополиса-Гастингса
Суть этого алгоритма основана на той же идее: мы хотим взять точку равномерно под графиком функции. Однако подход теперь другой: вместо того чтобы пытаться накрыть всё распределение «колпаком» функции q, мы будем действовать изнутри: будем строить случайное блуждание под графиком функции, переходя от одной точки к другой, и время от времени брать текущую точку блуждания в качестве сэмпла. Поскольку в данном случае это случайное блуждание является марковской цепью (т.е. его следующая точка зависит только от предыдущей, а памяти никакой нету), этот класс алгоритмов называется ещё MCMC-сэмплированием (Markov chain Monte Carlo). Чтобы доказать, что алгоритм Метрополиса-Гастингса действительно работает, нужно знать свойства марковских цепей; но мы сейчас ничего формально доказывать не собираемся, так что я просто целомудренно оставлю ссылку на вики.
Фактически же алгоритм похож на всё ту же выборку с отклонением, но с важным отличием: раньше распределение q было едино для всего пространства, а теперь оно будет локальным и будет меняться со временем, зависеть от текущей точки блуждания. Как и прежде, мы рассматриваем семейство пробных распределений 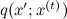 , где
, где 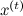 — текущее состояние. Но теперь q не должно быть приближением p, а должно просто быть каким-нибудь сэмплируемым распределением, которое сосредоточено в окрестности текущей точки — например, хорошо подходит сферический гауссиан с небольшой дисперсией. Кандидат в новое состояние x‘ теперь будет сэмплироваться из
— текущее состояние. Но теперь q не должно быть приближением p, а должно просто быть каким-нибудь сэмплируемым распределением, которое сосредоточено в окрестности текущей точки — например, хорошо подходит сферический гауссиан с небольшой дисперсией. Кандидат в новое состояние x‘ теперь будет сэмплироваться из 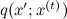 . Очередная итерация алгоритма начинается с состояния
. Очередная итерация алгоритма начинается с состояния 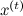 и заключается в следующем:
и заключается в следующем:
- выбрать x‘ по распределению
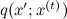 ;
; - вычислить

(не надо пугаться, для симметричных распределений, например гауссиана, равно 1, это просто поправка на асимметрию);
для симметричных распределений, например гауссиана, равно 1, это просто поправка на асимметрию); - С вероятностью a (1, если a>1)
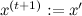 , иначе
, иначе 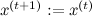 .
.
Суть в том, что мы переходим в новый центр распределения, если примем очередной шаг, и получается случайное блуждание, зависящее от распределения p: мы всегда принимаем шаг, если в эту сторону функция плотности увеличивается, и иногда отвергаем, если уменьшается (отвергаем не всегда, потому что нам надо уметь выходить из локальных максимумов и блуждать под всем графиком p). Замечу, кстати, что когда шаг отвергается, мы не просто отбрасываем новую точку, а повторяем второй раз то же самое x(t) — таким образом высока вероятность повторять сэмплы вокруг локальных максимумов распределения p, что соответствует большей плотности.
И снова картинка — вот типичное блуждание на плоскости под графиком смеси двух двумерных гауссианов:
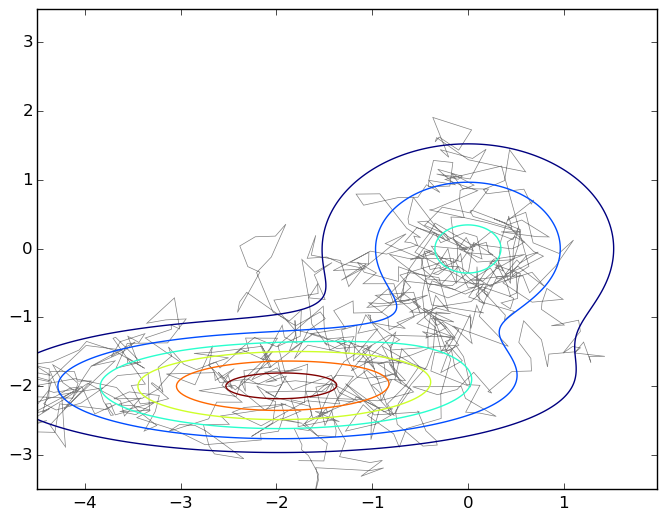
Чтобы подчеркнуть, насколько это на самом деле простой алгоритм, я приведу код, которым был порождён этот график.
import numpy as np import matplotlib.pyplot as plt import matplotlib.patches as patches import matplotlib.path as path import matplotlib.mlab as mlab import scipy.stats as stats delta = 0.025 X, Y = np.meshgrid(np.arange(-4.5, 2.0, delta), np.arange(-3.5, 3.5, delta)) z1 = stats.multivariate_normal([0,0],[[1.0,0],[0,1.0]]) z2 = stats.multivariate_normal([-2,-2],[[1.5,0],[0,0.5]]) def z(x): return 0.4*z1.pdf(x) + 0.6*z2.pdf(x) Z1 = mlab.bivariate_normal(X, Y, 1.0, 1.0, 0.0, 0.0) Z2 = mlab.bivariate_normal(X, Y, 1.5, 0.5, -2, -2) Z = 0.4*Z1 + 0.6*Z2 Q = stats.multivariate_normal([0,0],[[0.05,0],[0,0.05]]) r = [0,0] samples = [r] for i in range(0,1000): rq = Q.rvs() + r a = z(rq)/z(r) if np.random.binomial(1,min(a,1),1)[0] == 1: r = rq samples.append(r) codes = np.ones(len(samples), int) * path.Path.LINETO codes[0] = path.Path.MOVETO p = path.Path(samples,codes) fig, ax = plt.subplots() ax.contour(X, Y, Z) ax.add_patch(patches.PathPatch(p, facecolor='none', lw=0.5, edgecolor='gray')) plt.show() Итак, мы получили случайное блуждание под графиком плотности p(x); на самом деле это ещё надо доказать, но в математику мы углубляться не будем, так что поверьте на слово. Что теперь делать с этим случайным блужданием, нам же нужны независимые сэмплы, а тут получается, что следующая точка блуждания заведомо лежит рядом с предыдущей, и никакой независимости нет и в помине?
Ответ простой: нужно брать не каждую точку, а только некоторые, отделённые друг от друга многими шагами. Поскольку это случайное блуждание, то если большая часть q сосредоточена в радиусе ε, а общий радиус, в котором сосредоточено p, равен D, то для получения независимого сэмпла нужно будет порядка 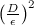 шагов. В это вы, опять же, можете поверить на слово, а можете вспомнить классическую задачку из курса теории вероятностей о том, как далеко за n шагов уйдёт точка, которая с равной вероятностью двигается налево и направо; уйдёт она в среднем на
шагов. В это вы, опять же, можете поверить на слово, а можете вспомнить классическую задачку из курса теории вероятностей о том, как далеко за n шагов уйдёт точка, которая с равной вероятностью двигается налево и направо; уйдёт она в среднем на 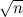 , так что логично, что шагов будет квадратичное число.
, так что логично, что шагов будет квадратичное число.
А теперь главная фишка: это квадратичное число зависит от радиусов двух распределений, но при этом совершенно не зависит от размерности. Сэмплирование по методу марковских цепей Монте-Карло в гораздо меньшей степени подвержено проклятию размерности, чем другие методы, которые мы обсуждали; именно поэтому оно и стало, можно сказать, золотым стандартом. На практике, правда, D оценить трудно, так что в конкретных реализациях обычно делают так: сначала некоторое достаточно число первых шагов, скажем 1000, отбрасывают (это называется burn-in, и это действительно важно, потому что начальная точка может попасть в неудачную область p, так что перед началом процесса надо точно убедиться, что мы уже ходили достаточно долго), а потом берут каждый n-й сэмпл, где n подбирают экспериментально, исходя из реально получающейся автокорреляции в последовательности сэмплов.
Сэмплирование по Гиббсу
И последний на сегодня алгоритм сэмплирования — сэмплирование по Гиббсу. Это на самом деле частный случай алгоритма Метрополиса-Гастингса, очень популярный и простой частный случай.
Идея сэмплирования по Гиббсу ну совсем простая: предположим, что мы находимся в очень большой размерности, вектор x очень длинный, и нам сложно выбирать весь сэмпл сразу, не получается. Давайте попробуем выбирать сэмпл не весь сразу, а покомпонентно. Тогда наверняка эти одномерные распределения окажутся проще, и сэмпл мы выберем.
Формально говоря, мы пробегаем по компонентам вектора 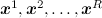 , на каждом шаге фиксируем все переменные, кроме одной, и выбираем последовательно
, на каждом шаге фиксируем все переменные, кроме одной, и выбираем последовательно 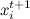 по распределению
по распределению
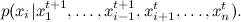
От общего случая блуждания по Метрополису-Гастингсу это отличается тем, что теперь мы двигаемся на каждом шаге вдоль одной из координатных осей; вот соответствующая картинка:
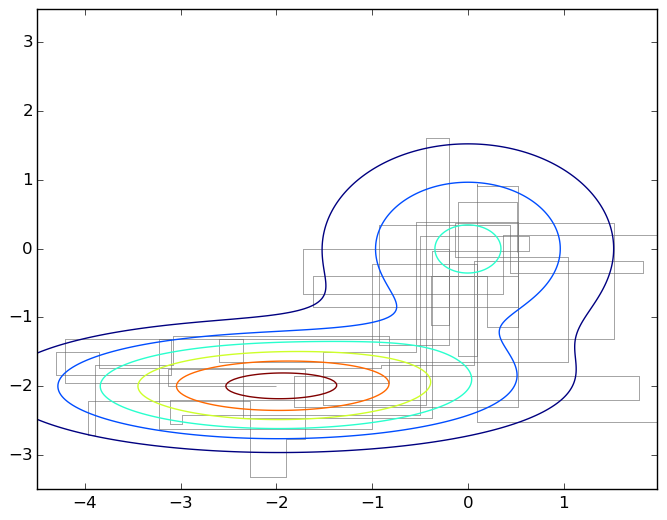
Сэмплирование по Гиббсу — это частный случай алгоритма Метрополиса для распределений 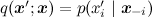 , и вероятность принятия каждого сэмпла получается всегда равна 1 (можете это доказать в качестве упражнения). Поэтому сэмплирование по Гиббсу сходится, и, так как это такое же случайное блуждание по сути, верна та же квадратичная оценка.
, и вероятность принятия каждого сэмпла получается всегда равна 1 (можете это доказать в качестве упражнения). Поэтому сэмплирование по Гиббсу сходится, и, так как это такое же случайное блуждание по сути, верна та же квадратичная оценка.
Для сэмплирования по Гиббсу не нужно никаких особенных предположений или знаний. Можно быстро сделать работающую модель, и поэтому это очень популярный алгоритм. Заметим ещё, что в больших размерностях может оказаться эффективнее сэмплить по несколько переменных сразу, а не по одной — например, часто бывает, что у нас двудольный граф из переменных, в которых все переменные из одной доли связаны со всеми переменными из другой доли (ну или со многими), а между собой не связаны. В такой ситуации сам Бог велел зафиксировать все переменные одной доли и просэмплировать все переменные в другой доле одновременно (это можно понимать буквально — поскольку при такой структуре все переменные одной доли условно независимы при условии другой, их можно сэмплировать независимо и параллельно), потом зафиксировать все переменные второй доли и так далее.
Заключение
Сегодня мы успели довольно много: мы поговорили о разных методах сэмплирования, которое является одним из основных инструментов приближённого вывода в сложных вероятностных моделях. Дальше я планирую развивать этот новый мини-цикл в сторону тематического моделирования, точнее, модели LDA (latent Dirichlet allocation, латентное размещение Дирихле). В следующей серии я расскажу о самой модели (кратко я её уже описывал, теперь можно поговорить более детально) и объясню, как для LDA работает сэмплирование по Гиббсу. А потом мы будем постепенно переходить к тому, как можно применять LDA и её многочисленные расширения для рекомендательных систем.
ссылка на оригинал статьи http://habrahabr.ru/company/surfingbird/blog/226677/
Добавить комментарий