В процессе разработки одного приложения столкнулся с необходимостью рисования эллипсов под произвольным углом в canvas на JavaScript. Пользоваться какими-либо фреймворками в столь простом проекте не хотелось, так что я отправился на поиски статьи-мануала на эту тему. Поиски не увенчались успехом, так что пришлось разбираться с задачей самостоятельно, и я решил поделиться с вами полученным опытом.Формализуем задачу. Нам требуется функция drawEllipse(coords, sizes, vector), где:
- coords — координаты центра эллипса — массив [x, y]
- sizes — длины большой и малой полуосей эллипса — массив [a, b]
В качестве основного средства для решения задачи были выбраны кривые Безье. Для построения такой кривой требуются четыре точки: начальная, конечная и две контрольные.
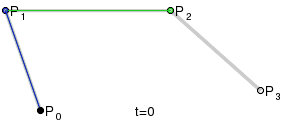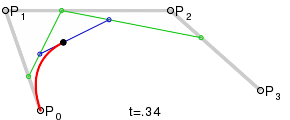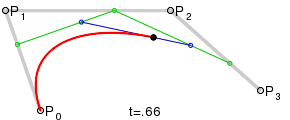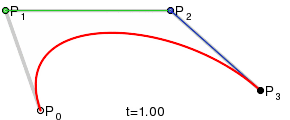
Наш искомый эллипс будет состоять из двух таких кривых, причем нетрудно догадаться, что вышеупомянутые точки у каждой из них будут вершинами прямоугольника. Попробуем построить наш эллипс.
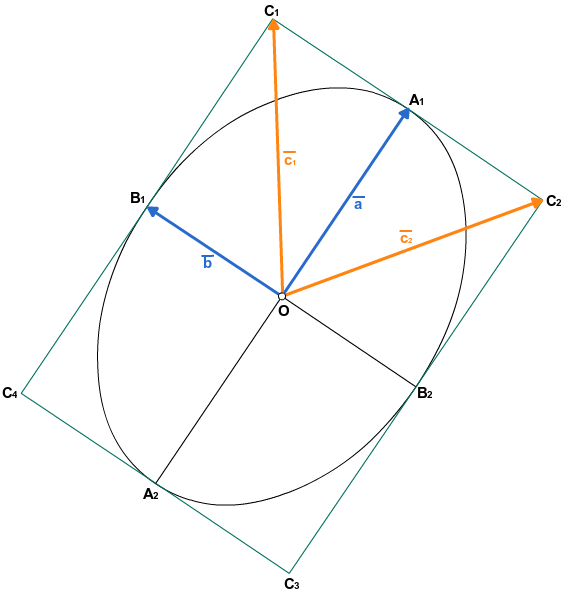
- Имеем некоторый вектор

Найдем единичный вектор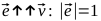
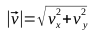
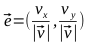
Найдем единичный вектор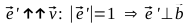
Для этого вспомним свойство скалярного произведения векторов обращаться в ноль в случае, если они перпендикулярны: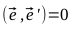
Таким образом: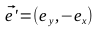
- Найдем векторы
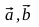 , точки A1, A2, B1, B2
, точки A1, A2, B1, B2
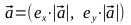
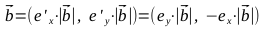

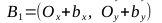
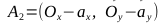
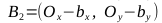
- Найдем векторы
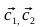 , точки C1, C2, C3, C4
, точки C1, C2, C3, C4
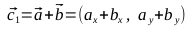
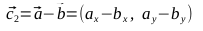
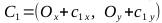
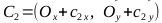
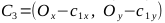
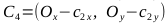
- Вспомним, что для рисования эллипса нам нужны две кривые Безье:
- 1-я имеет начальную точку B1, конечную B2, проходит через точку A1
- 2-я имеет начальную точку B2, конечную B1, проходит через точку A2
Вспомним также, что для построения кривых Безье нам требуются контрольные точки. Недолго думая, я сначала подставил в качестве таковых вершины прямоугольника, в который вписан эллипс. Это решение оказалось ошибкой, ведь если мы рассмотрим построение кривой Безье, то обнаружим, что она не касается отрезка, соединяющего две контрольные точки.
Изобразим момент построения кривой Безье в точке, в которой она (кривая) будет наиболее близка к отрезку между контрольными точками. В нашем случае это будет выглядеть так: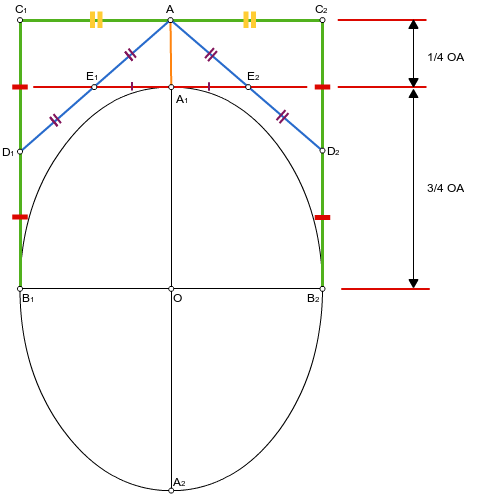
Из рисунка очевидно, что расстояние от этой точки (A1) до отрезка между контрольными точками (C1, C2) будет составлять четверть от расстояния между центром искомого эллипса (O) и тем же отрезком (C1, C2), то есть:

- Решим уравнение
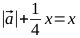
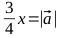
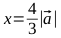
Таким образом, для получения эллипса с нужными параметрами нам необходимо умножить вектор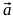 на параметр
на параметр 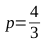 , после чего вернуться к вычислениям, описанным в пунктах 1-4. В результате получаем наборы точек (B1, C1, C2, B2 и B2, C3, C4, B1) для построения двух кривых Безье, вместе представляющих искомую фигуру.
, после чего вернуться к вычислениям, описанным в пунктах 1-4. В результате получаем наборы точек (B1, C1, C2, B2 и B2, C3, C4, B1) для построения двух кривых Безье, вместе представляющих искомую фигуру.
Собственно демо и код:
function drawEllipse(ctx, coords, sizes, vector) { var vLen = Math.sqrt(vector[0]*vector[0]+vector[1]*vector[1]); // вычисляем длину вектора var e = [vector[0]/vLen, vector[1]/vLen]; // единичный верктор e || vector var p = 4/3; // параметр var a = [e[0]*sizes[0]*p, e[1]*sizes[0]*p]; // находим вектор a, используя параметр var b = [e[1]*sizes[1], -e[0]*sizes[1]]; // находм вектор b // находим точки A1, B1, A2, B2 var dotA1 = [coords[0]+a[0], coords[1]+a[1]]; var dotB1 = [coords[0]+b[0], coords[1]+b[1]]; var dotA2 = [coords[0]-a[0], coords[1]-a[1]]; var dotB2 = [coords[0]-b[0], coords[1]-b[1]]; // находим вектора c1, c2 var c1 = [a[0]+b[0], a[1]+b[1]]; var c2 = [a[0]-b[0], a[1]-b[1]]; // находим точки C1, C2, C3, C4 var dotC1 = [coords[0]+c1[0], coords[1]+c1[1]]; var dotC2 = [coords[0]+c2[0], coords[1]+c2[1]]; var dotC3 = [coords[0]-c1[0], coords[1]-c1[1]]; var dotC4 = [coords[0]-c2[0], coords[1]-c2[1]]; // рисуем наш эллипс ctx.strokeStyle = 'black'; ctx.beginPath(); ctx.moveTo(dotB1[0], dotB1[1]); // начальная точка ctx.bezierCurveTo(dotC1[0], dotC1[1], dotC2[0], dotC2[1], dotB2[0], dotB2[1]); // рисуем кривую Безье ctx.bezierCurveTo(dotC3[0], dotC3[1], dotC4[0], dotC4[1], dotB1[0], dotB1[1]); // и вторую из точки, где закончили рисовать первую ctx.stroke(); ctx.closePath(); // возвращаем вектору a изначальную длину var a = [e[0]*sizes[0], e[1]*sizes[0]]; // отрисовываем красным отрезки от ближайших друг к другу и наиболее далеких друг от друга точек эллипса, чтобы проверить, правильно ли мы отобразили запрошенный эллипс ctx.beginPath(); ctx.moveTo(coords[0]+a[0], coords[1]+a[1]); ctx.lineTo(coords[0]-a[0], coords[1]-a[1]); ctx.moveTo(coords[0]+b[0], coords[1]+b[1]); ctx.lineTo(coords[0]-b[0], coords[1]-b[1]); ctx.strokeStyle = 'red'; ctx.stroke(); ctx.closePath(); } 
ссылка на оригинал статьи http://habrahabr.ru/post/255485/

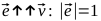
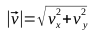
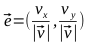
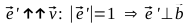
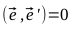
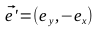
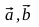 , точки A1, A2, B1, B2
, точки A1, A2, B1, B2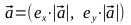
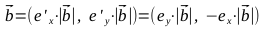

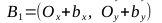
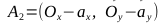
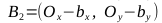
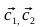 , точки C1, C2, C3, C4
, точки C1, C2, C3, C4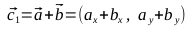
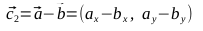
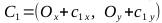
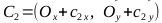
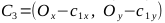
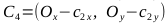


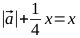
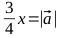
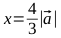
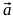 на параметр
на параметр 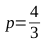 , после чего вернуться к вычислениям, описанным в пунктах 1-4. В результате получаем наборы точек (B1, C1, C2, B2 и B2, C3, C4, B1) для построения двух кривых Безье, вместе представляющих искомую фигуру.
, после чего вернуться к вычислениям, описанным в пунктах 1-4. В результате получаем наборы точек (B1, C1, C2, B2 и B2, C3, C4, B1) для построения двух кривых Безье, вместе представляющих искомую фигуру.
Добавить комментарий