Арбелос

Скачать статью в виде документа Mathematica (NB), CDF-файла или PDF.
Выражаю огромную благодарность Кириллу Гузенко за помощь в переводе.

---

В этой статье систематически проверяются некоторые свойства фигуры, известной с древних времён, называемой арбелос. Она включает в себя несколько новых открытий и обобщений, представленных автором данной работы.

Введение

Будучи мотивирован вычислительными преимуществами, которыми обладает Mathematica, некоторое время назад я решил приступить к исследованию свойств арбелоса — весьма интересной геометрической фигуры. С тех пор я был впечатлен большим количеством удивительных открытий и вычислительных проблем, которые возникали из-за всё расширяющегося объёма литературы, касающейся этого примечательного объекта. Я вспоминаю его сходство с нижней частью культового велосипеда пенни-фартинг из The Prisoner (телесериал 1960-х), шутовской шапкой Панча (знаменитых Punch and Judy) и символом инь-ян с одной перевёрнутой дугой; см. рис. 1. В настоящее время существует специализированный каталог архимедовых кругов (круги, содержащиеся в арбелосе) [1] и важные применения свойств арбелоса, которые лежат вне поля математики и вычислительных наук [2].

Многие известные исследователи занимались этой темой, в том числе Архимед (убитый римским солдатом в 212 г. до н.э.), Папп (320 г. н.э.), Кристиан О. Мор (1835-1918), Виктор Тебо (1882-1960), Леон Банкофф (1908-1997), Мартин Гарднер (1914-2010). С недавних пор свойствами арбелоса занимаются Клейтон Додж, Питер Ай. Ву, Томас Шох, Хироши Окумура, Масаюки Ватанабе и прочие.

Леон Банкофф — человек, который привлекал всеобщее внимание к арбелосу в последние 30 лет. Шох привлёк внимание Бэнкоффа к арбелосу в 1979 году, открыв несколько новых архимедовых кругов. Он послал 20-страничную рукописную работу Мартину Гарднеру, который направил её Бэнкоффу, который затем отправил 10-страничный фрагмент копии рукописи Доджу в 1996 году. Из-за смерти Бэнкоффа запланированная совместная работа была прервана, пока Додж не сообщил о некоторых новых открытиях [3]. В 1999 году Додж сказал, что ему потребуется от пяти до десяти лет, чтобы отсортировать весь материал, которым он располагает, разложив всё это дело по стопкам. В настоящее время эта работа все ещё продолжается. Не удивительно, что в четвертом томе The Art of Computer Programming, сказано о том, что важная работа требует большого количества времени.

Рис. 1. Велосипед пенни-фартинг, куклы Панч и Джуди, физический арбелос.

Арбелос (“нож сапожника” в греческом языке) назван так из-за своего сходства с лезвием ножа, использующегося сапожниками (Рис. 1). Арбелос — плоская область, ограниченная тремя полуокружностями и общей базовой линией (рис. 2). Архимед, вероятно, был первым, кто начал изучать математические свойства арбелоса. Эти свойства описаны в теоремах с 4-ой по 8-ую его книги Liber assumptorum (или Книги лемм). Возможно, эту работу написал не Архимед. Сомнения появились после перевода с арабского Книги лемм, в которой Архимед упоминается неоднократно, но ничего не сказано о его авторстве (однако, существует мнение, что эта книга — подделка [4]). Книга Лемм так же содержит знаменитую архимедову Problema Bovinum [5].

Эта статья направлена на систематическое изложение некоторых свойств арбелоса и не носит исчерпывающий характер. Наша цель состоит в том, чтобы выработать единую вычислительную методологию для того, чтобы преподнести данные свойства в формате обучающей статьи. Все свойства выстроены в рамках определённой последовательности и представлены с доказательствами. Эти доказательства были реализованы посредством тестирования эквивалентных вычисляемых утверждений. В ходе выполнения данной работы автором было совершено несколько открытий и сделано несколько обобщений.

Мы называем наибольший полукруг верхней дугой, а два маленьких — левосторонней и правосторонней дугами, или просто боковыми дугами, если нет необходимости их различать. Мы используем и соответственно для обозначения их радиусов, а радиус верхней дуги обозначается как . Отрезок между двумя точками неориентирован и простирается от одной точки до другой, в то время как прямая, содержащая две точки, является бесконечной и находится и за пределами этих двух точек. Классическая неточность в обозначениях — использовать для обозначения как самого отрезка, соединяющего точки и , так и его длины в зависимости от контекста; современная нотация велит писать для обозначения длины отрезка.

Эта функция задаёт арбелос.

Так можно нарисовать сам арбелос.

Рис 2. Арбелос.

Свойство 1
Периметр арбелоса равен периметру наибольшей окружности.

Свойство 2
Площадь арбелоса равна площади круга с диаметром .

Это лемма под номером 4 из Книги лемм (рис. 3) [7, 8].

Эти два свойства легко доказываются путём вычисления представленной ниже логической конструкции, состоящей из двух равенств.

Функция drawpoints отображает заданные точки красными кружками.

Рис. 3. Площадь круга диаметра (радикального круга) равна площади арбелоса.

Радикальный круг

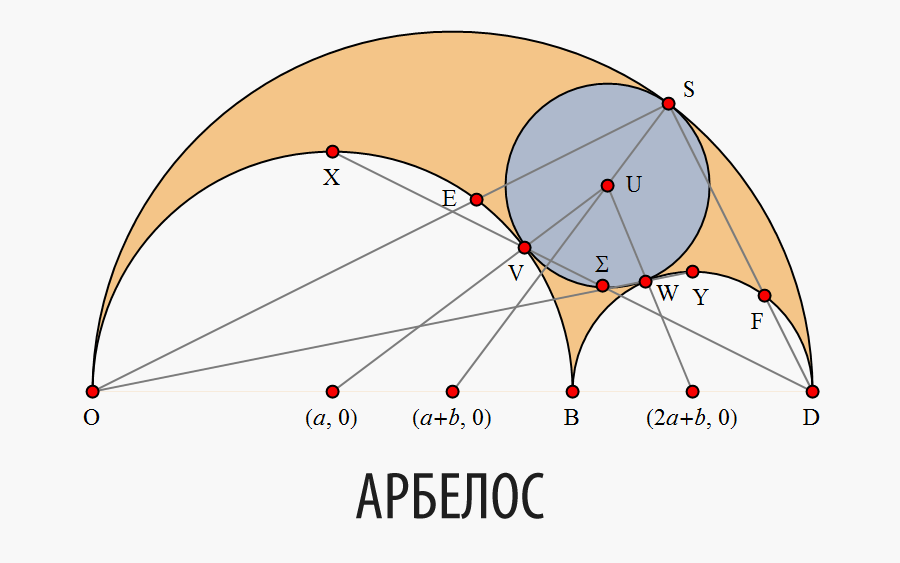
Круг на риc. 3 называется радикальным кругом арбелоса, а линия называется его радикальной осью (эта терминология будет разъяснена в Обобщениях). Обозначим и проименуем точки, линии, окружности и координаты, которые нам понадобятся для иллюстрации свойств 3-11 и 25-26 (рис. 4).

Рис. 4. Обозначения координат, линий и окружностей, упомянутых в свойствах 3-11 и 25-26.

Свойство 3
Линии и перпендикулярны и касаются боковых дуг в точках и , пересекая их общую касательную.

Чтобы доказать перпендикулярность линий и , вычислим скалярное произведение векторов и .

Используем полученный результат для получения угла наклона прямой .

Теорема 1
Уравнение касательной к левой дуге в точке :

а уравнение касательной к правой дуге в точке :

Функция PQ находит координаты точек касания и путём решения системы из четырех уравнений, которые задают их положения на дугах и углы наклона касательных согласно теореме 1.

Помимо PQ, в данной статье встречаются так же и нижеперечисленные обозначения точек и величин: VWS, HK, U, EF, IJr и LM.

Функция dSq вычисляет квадрат расстояния между двумя заданными точками.

Свойство 4
Точки и находятся на радикальной окружности.

Так как является диаметром радикальной окружности, нам нужно всего лишь доказать равенство расстояний от и до центра радикальной окружности, который обозначается как .

Свойство 5
Пусть линия пересекает верхнюю дугу в точках и . Тогда и лежат на окружности c центром в и радиусом .

Мы получаем координаты точек и , решая систему уравнений, которая задаёт их расположение на верхней дуге и на линии .

Это доказывает свойство 5 путём проверки того, что расстояния от и до равны расстоянию от до .

Свойство 6
Прямая параллельна прямой .

Это эквивалентно тому, что определитель векторов и (их векторное произведение) равен нулю.

Свойство 7
Прямая перпендикулярна прямой .

Это эквивалентно тому, что скалярное произведение векторов и равно нулю.

Обозначим окружность с центром в и радиусом как .

Свойство 8
Пары , и , — представляют собой пары взаимно обратных точек для окружности .

Обратной точкой к точке в окружности (при этом ) является такая точка , что выполняется равенство [9]. Функция inversion реализует эту идею.

Так можно доказать свойство 8, подставив вместо .

Свойство 9
Исследуем окружность обратных точек . Для данной окружности точки , , совпадают со своими обратными точками. Отрезок является обратным для дуги , а отрезок — инверсия дуги . Дуги и так же являются взаимно обратными. Радикальная окружность есть инверсия прямой .

Свойство 10
Прямые и есть касательные к радикальной окружности.

Это утверждение аналогично тому, что соответствующие дуги (то есть их касательные) перпендикулярны радакальной окружности (его касательным в точках пересечения). Согласно свойству 8, дуги являются перпендикулярными окружности с диаметром , если они проходят через пару обратных точек [10,11].

Свойство 11
— прямоугольник.

Это один из сюрпризов Бэнкоффа (Bankoff’s surprises) [12,13,14]. Если все четыре точки лежат на радикальной окружности, нам достаточно доказать, что делит пополам .

Представленная ниже демонстрация со слайдером (реализованным посредством функции Manipulate) иллюстрирует свойства 3-11. Самый лёгкий способ задать точки P, Q, H, K — скопировать и вставить соответствующие для них формулы.

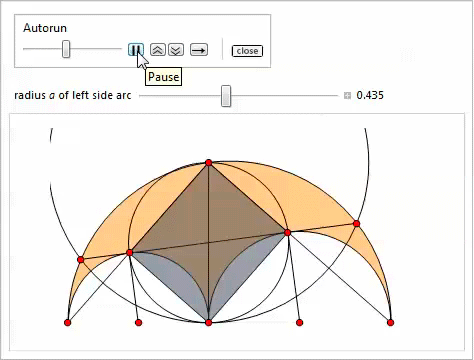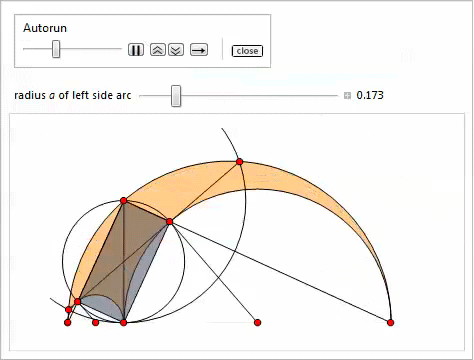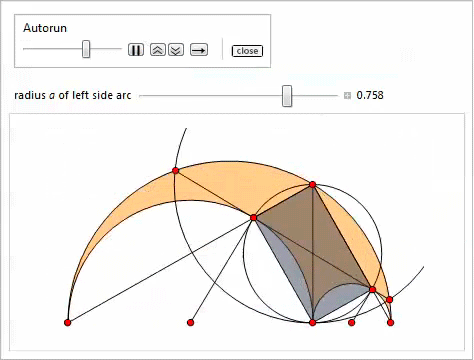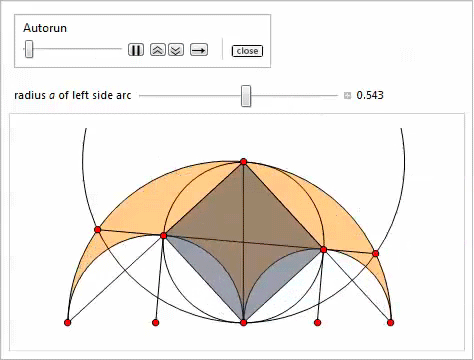
Вписанная окружность

Теперь рассмотрим окружность, касательную к боковым дугам и верхней дуге — вписанную окружность в арбелос с точками касания , , и (см. рис. 5) [15, 16]. Обозначим так же вершины дуг точками и соответственно.

Рис. 5. Вписанная окружность , координаты, прямые и точки, указанные на рисунке, фигурируют в свойствах с 12 по 15.

Шестое утверждение из Книги лемм включает так же радиус вписанной окружности, обозначаемый как . Функция Uвычисляет координаты центра вписанной окружности и её радиус .

Координаты точек касания , , и определяются через пересечение линий, соединяющих центры дуг арбелоса, со вписанной окружностью.

Свойство 12
Точки , , и лежат на одной прямой. Точки , , и лежат на одной прямой. Линии и пересекаются в точке , которая лежит на вписанной окружности.

Первые два утверждения можно доказать, используя критерий определителя для проверки коллинеарности.

Пусть будет точкой пересечения линий и . Доказав, что расстояние от этой точки до равно , мы докажем третье утверждение.

Свойство 13
Точки , , , и лежат на окружности с центром в . Аналогично, точки , , , и лежат на окружности с центром в .

Представленная ниже демонстрация с Manipulate иллюстрирует свойство 13 [17]. Опция Bankoff circle покажет вписанную окружность в треугольник, который соединяет центры дуг. Это иллюстрирует свойство 23.

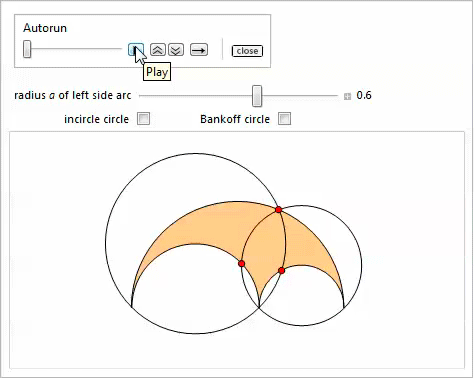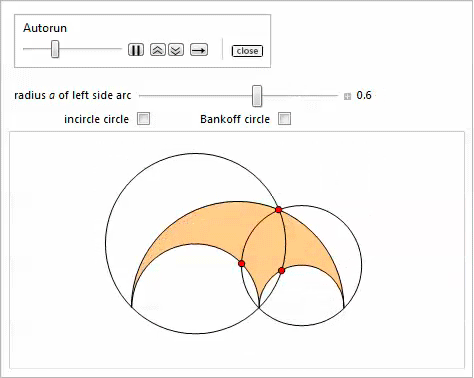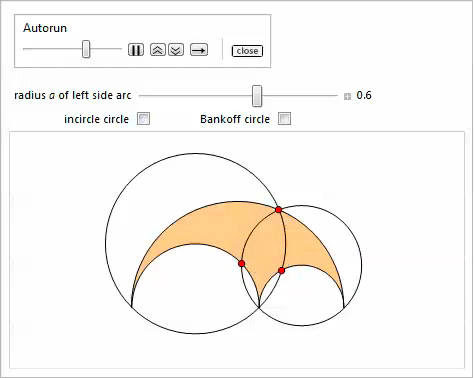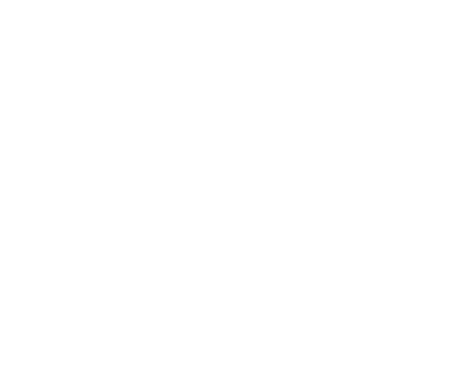
Свойство 14
Пусть — диаметр вписанной окружности, параллельный , а – проекция на . Прямоугольник между отрезками и — квадрат.

Данное свойство проиллюстрировано в следующей демонстрации с Manipulate и легко может быть проверена следующим выражением.

Свойство 15
Пусть и — пересечения линий и с боковыми дугами. Тогда — квадрат практически такого же размера, что и квадрат, который упоминался в свойстве 14.

Сперва получим точки и как пересечения соответствующих линий и дуг, а затем сохраним результат в переменной replaceEF.

Докажем свойство 15, сделав равным вектору, получаемому вращением вокруг на 90° и сделав равным вектору, получаемому перемещением через .

Учитывая и , нижеследующий график сравнивает размеры двух квадратов.

Демонстрация с Manipulate иллюстрирует свойства 14 и 15.

Близнецы

Рассмотрим два серых круга, которые касаются радикальной оси, а так же боковые и верхние дуги на рис. 6. Они называются близнецами, или архимедовыми окружностями. В связи с нижеследующим замечательным свойством, они были хорошо изучены. Множество их необычных черт были освещены в нашем списке свойств [3, 18, 19].

Рис. 6. Близнецы.

Свойство 16
Два круга, которые перпендикулярны радикальной оси, верхней и боковым дугам арбелоса имеют одинаковый радиус.

Это свойство идёт как пятое утверждение в Книге лемм. Решая данную систему из шести уравнений, мы находим значения их радиусов, проверяем, что они равны и находим координаты их центров , .

Эти четыре решения дают центры, сгруппированные попарно: , , , где и являются отображениями и на диаметр арбелоса; только последнее выражение является допустимым. Это так же показывает, что близнецы действительно одного и того же радиуса . Любая окружность, у которой радиус имеет ту же длину, что и у близнецов, называется архимедовой. Можно провести довольно наглядную аналогию для , если представить, что и — (электрические) сопротивления. Тогда — сопротивление, получаемое путём параллельного соединения и ; то есть . Функция IJr вычисляет координаты центров и длину радиуса близнецов.

Свойство 17
Площадь арбелоса равна площади наименьшего круга, который охватывает близнецов.

Рассмотрим окружность, касательную к обоим близнецам, с центром в точке и радиусом . Тогда у нас будут два возможных значения для .

Чтобы найти экстремум для , приравняем производные обоих уравнений к нулю и решим их относительно .

Таким образом, центры наименьшей и наибольшей окружностей, касательных к близнецам, лежат на радикальной оси. Более того, их центры лежат в одной точке, что следует из решения данного выражения.

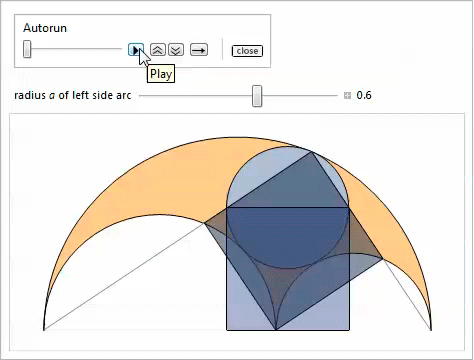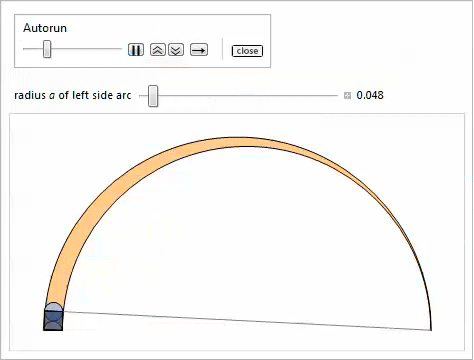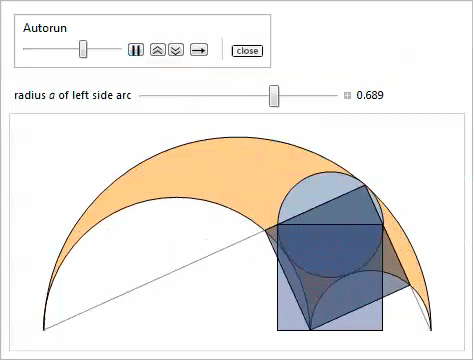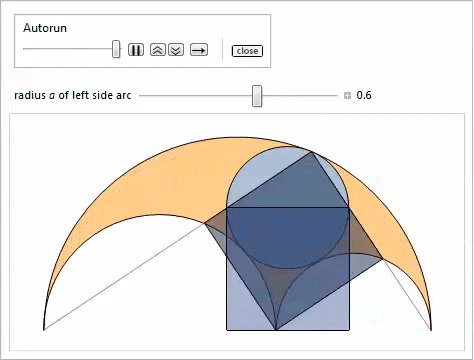
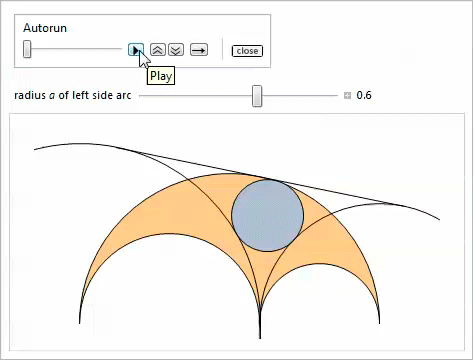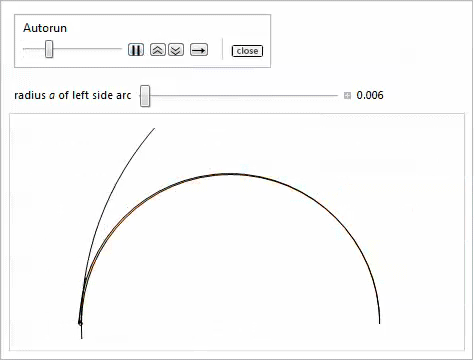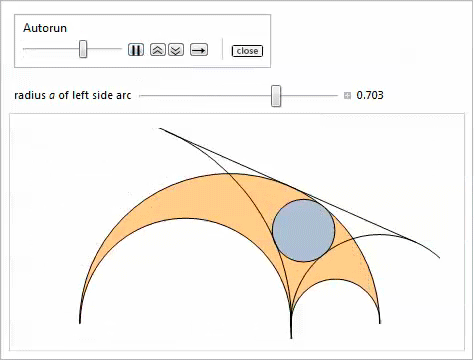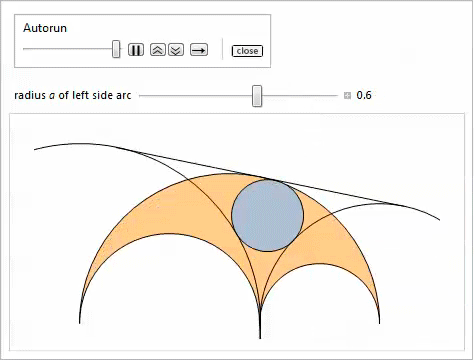
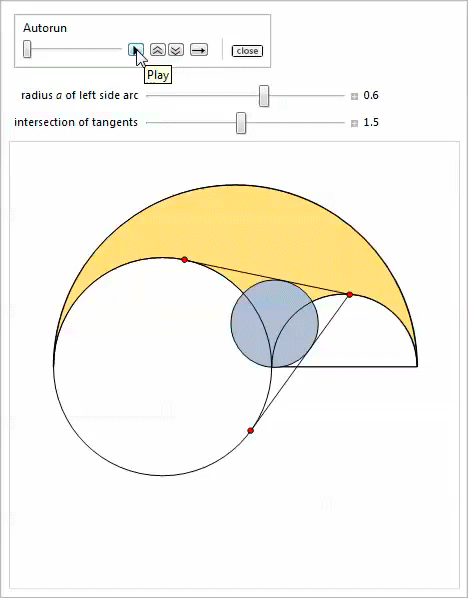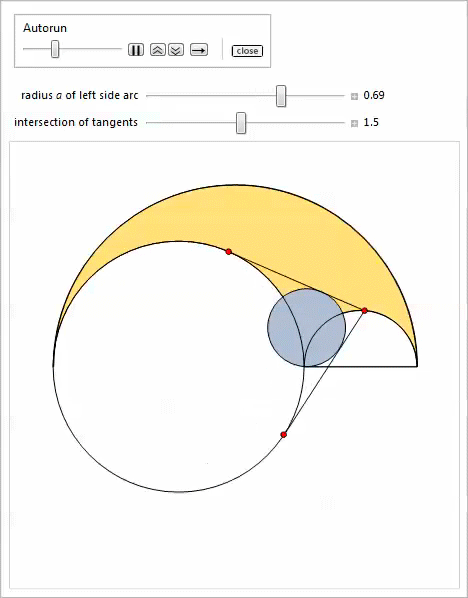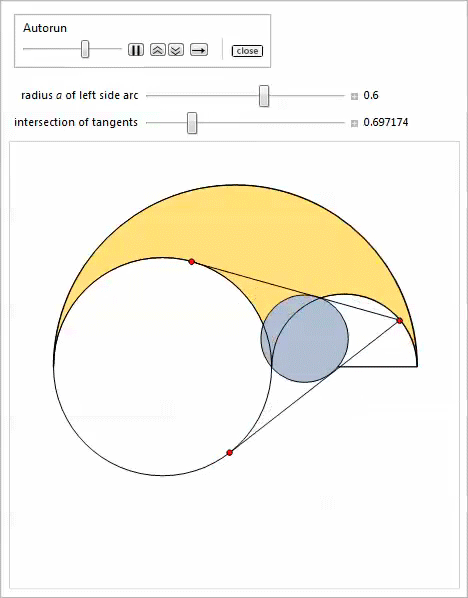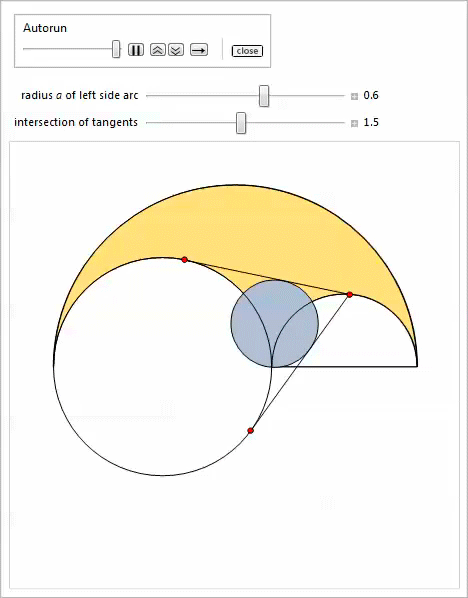
Таким образом, используя свойство 2, мы доказываем, что наибольшая касательная окружность, которая является самой малой из тех, что содержит близнецов, удовлетворяет свойству 17. Нижеследующая демонстрация с Manipulate показывает окружности, касательные к близнецам, при этом можно регулировать радиус левой боковой дуги.

Следующий график сравнивает радиусы двух окружностей, касательных к близнецам, с центрами на радикальной оси.

Рис. 7. Обозначения точек и отрезков, которые будут фигурировать в свойствах 18-24.

Свойство 18
Общая касательная к левой дуге и близнецу (точка касания — ) проходит через точку . Аналогично, общая касательная к правой дуге и близнецу (точка касания — ) проходит через точку (см. рис. 7).

Так можно вычислить точки касания и .

Используя теорему 1, докажем оба утверждения.

Свойство 19
Длина равна длине . Длина равна длине .

Докажем оба утверждения одновременно.

Однако, точки , , и не лежат на окружности с центром в , равно как и точки , , и не лежат на окружности с центром в ; иначе следующее выражение было бы равно нулю.

Свойство 20
Линия делит отрезок пополам. Линия делит отрезок пополам.

Поскольку длина отрезка — ордината , и длина отрезка — ордината , достаточно проверить, что центры этих отрезков лежат на указанных линиях, проверкой углов наклона.

Свойство 21
Два синих круга с диаметрами на , проходящие через и касательные к и являются архимедовыми.

Эти круги — четвёртый и пятый архимедовы круги, открытые Бэнкоффом [20]. Чтобы проверить это свойство, используем следующий результат [21]:

Теорема 2
Расстояние от точки до прямой, проходящей через точки и есть:

Данное ориентированное расстояние будет положительным, если треугольник пересекается против часовой стрелки, и отрицательным в противном случае. Данное отображение реализует функция dAB.

Пусть и — соответственно центр и радиус голубого круга по левую сторону от точки (рис. 7). Решая следующую систему, найдём значение .

Аналогично можно вычислить радиус синего круга справа от , который равняется .

Таким образом, оба круга — архимедовы, как и было сказано ранее. Следующая демонстрация с Manipulate содержит близнецов и два других круга.

Свойство 22
Окружность, проходящая через точки , , и на рис. 5, которую называют окружностью Бэнкоффа — является архимедовой окружностью.

Архимед открыл исходные два близнеца; Бэнкофф дополнил их третьей окружностью, открытой в 1950 году [22]. Координаты центра окружности Бэнкоффа можно получить, вычислив расстояния от до точек , , и .

Свойство 23
Окружность Бэнкоффа — вписанная в треугольник, который образован соединением центров боковых дуг и центра вписанной в арбелос окружности.

Используя теорему 2 для вычисления расстояния от до сторон треугольника, докажем это свойство (так как dAB вычисляет ориентированное расстояние, порядок расположения аргументов, описывающих линию, является весьма важным).

Свойство 24
Окружность , касательная к окружностям , и верхней дуге — архимедова.

Таким образом можно вычислить значения и .

Окружность — единственная, для которой ордината – положительна. Следует заметить, что — не радикальная ось.

Свойство 25
Окружности и , касательные к радикальной оси и проходящие через и соответственно, являются архимедовыми (см. рис. 4).

Свойство 26

Окружность , касательная к прямой и верхней дуге в точке — архимедова (см. рис. 4).

Окружность с центром в точке и радиусом , касательная к такова, что расстояние от до равно , и уравнение принимает следующий вид:

Так как окружность проходит через ,

Так как окружность касательна к верхней дуге,

Тут мы используем явные выражения для , , и которые удовлетворяют данным трём равенствам.

Свойство 27
Рассмотрим два отрезка (обозначены красным), соединяющих центр верхней дуги с вершинами левой и правой дуг арбелоса. Эти отрезки равны и перпендикулярны. Касательные окружности и в точках и к этим отрезкам и верхней дуге архимедовы (см. рис. 8).

Это свойство было обнаружено летом 1998 года [23].

Рис. 8. Две пары архимедовых окружностей из свойства 27.

Наклонные близнецы

Было показано, что есть архимедовы окружности, отличные от близнецов, а именно — окружности Бэнкоффа, которые фигурируют в свойствах 21-27. Есть так же неархимедовы близнецы — пары окружностей с одинаковым радиусом, отличным от радиуса близнецов, которые появляются в определённых областях арбелоса.

Открытие наклонных близнецов возникло из предположения о том, что помимо того, чтобы касаться боковой и верхней дуг, окружности-близнецы могут касаться друг друга, и при этом необязательно касаться радикальной оси. Очевидно, что существует бесконечное число решений, если мы не требуем, чтобы эти окружности были одного радиуса. Идея была следующая: если мы начнём с предположения о том, что они равного радиуса, мы могли бы в результате обнаружить, что они касаются радикальной оси. Это оказалось не так. Рассмотрим окружности с центрами в точках и и с одинаковым радиусом . Значение может быть получено путем решения системы из пяти уравнений.

Эти выражения включают квадратные корни, отличающиеся знаком. Положительные корни расходятся на и отклоняются.

Остальные — сходятся.

Подытожим: наклонные близнецы действительно равны и их общий радиус равен

Следующее сравнение между радиусами обычных и наклонных близнецов показывает, что они отличаются весьма незначительно.

Так можно получить координаты центров наклонных близнецов.

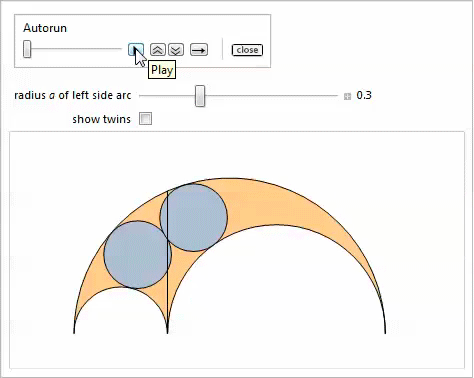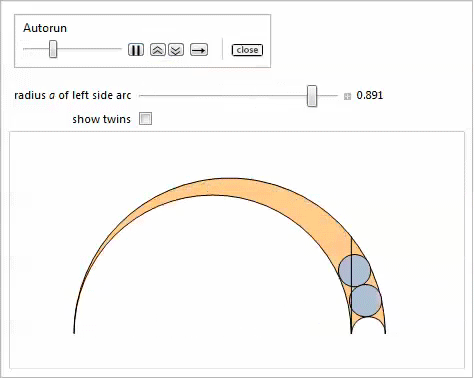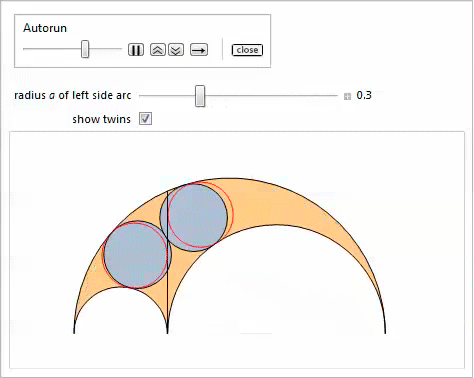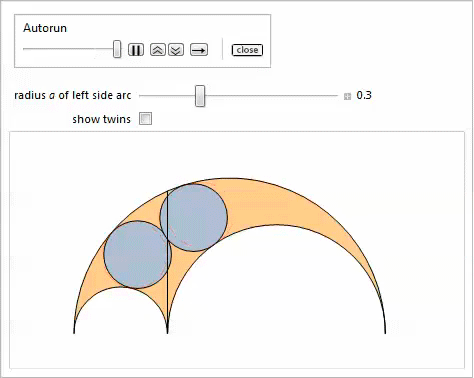
На представленной ниже демонстрации с Manipulate показаны наклонные близнецы и, опционально — близнецы, которые получаются при изменении параметра .

Обобщения

В этом разделе мы обобщаем геометрию арбелоса, позволив дугам пересекаться и рассматривая трёхмерный вариант. Чтобы задать контекст первого из обобщений, введём понятие радикальной оси для двух окружностей.

Радикальные оси

Пусть — точка, а — окружность . Степень отношения к определяется некоторым вещетвенным числом . Степень положительна, равна нулю или отрицательна при положении снаружи, на или внутри , соответственно [12]. Пусть ; если точки, принадлежащие , удовлетворяют уравнению , то мы сможем определить степень , вычислив . То же самое можно получить, если , когда окружность вырождается в прямую, и в этом случае знак указывает на то, где находится относительно прямой: над ней, на ней или под ней соответственно.

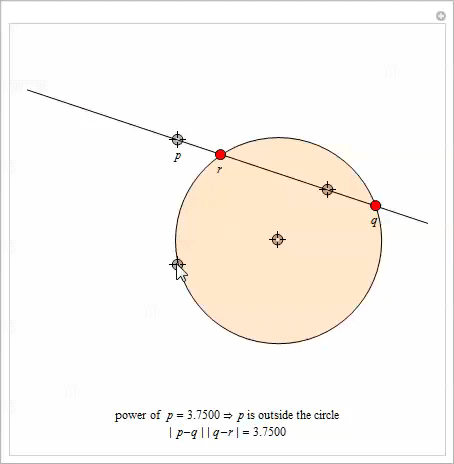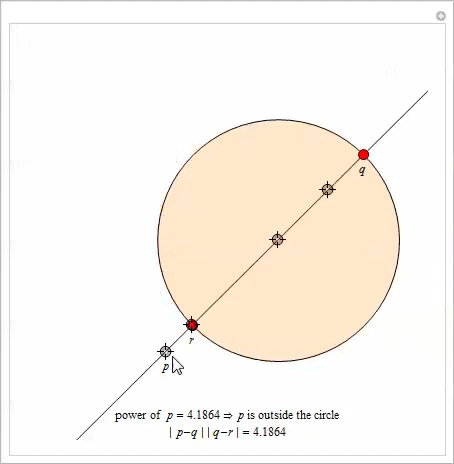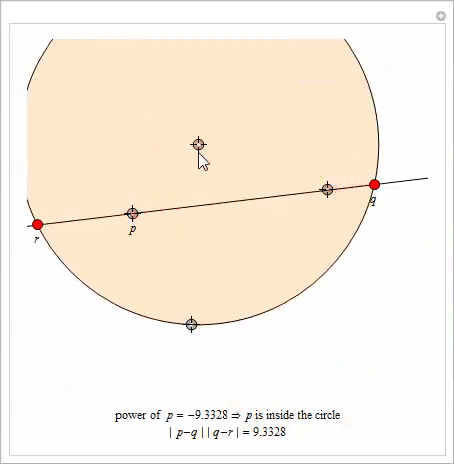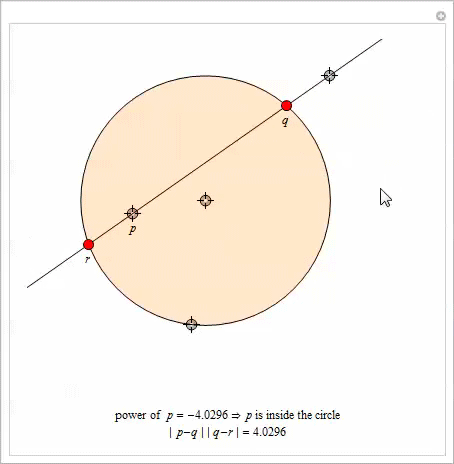
Вот очень интересное свойство степени точки. Пусть даны окружность и некоторая точка . Выберем произвольную прямую, проходящую через и пересекающую окружность в точках и . Тогда произведение зависит только от и не зависит от выбора прямой, проходящей через . Это произведение равно степени .

В приведенной ниже демонстрации с Manipulate имеется четыре локатора для изменения размеров окружности, положения и наклона линии, проходящей через .

Пусть даны две окружности с центрами в разных точках. Их радикальные оси определяются как прямые, содержащие все точки, которые имеют одинаковые степени по отношению к каждой из окружностей. Доказательство данного утверждения можно найти в [10].

Теорема 3
Если две окружности пересекаются в точках и , то тогда их радикальные оси являются общей секущей . Если две окружности касаются , то тогда их радикальные оси являются их общей касательной в точке .

Следствие 1
Пусть даны три окружности с центрами, не лежащими на одной прямой. Тогда их радикальные оси будут попарно параллельны и не будут совпадать.

Теорема 4
Радикальная ось двух окружностей есть геометрическое место точек, из которых проведенные к ним касательные имеют одинаковую длину.

Представленная ниже демонстрация с Manipulate показывает две окружности; одна закреплена, а размер и центр другой окружности можно изменять, перемещая локатор и меняя положение слайдера, который отвечает за радиус. Можно использовать другой слайдер для изменения положения красной точки на радикальной оси чтобы проиллюстрировать теорему 4.

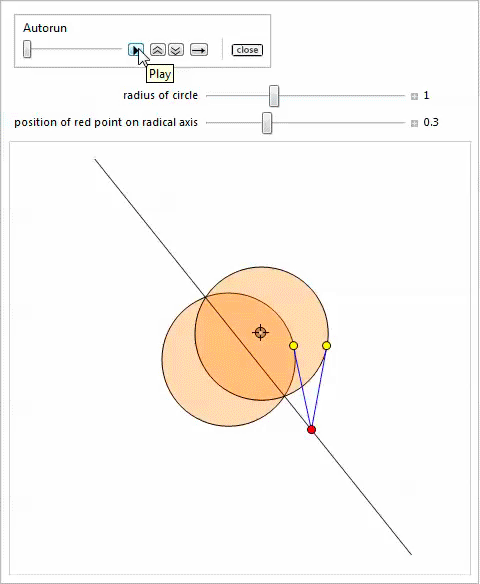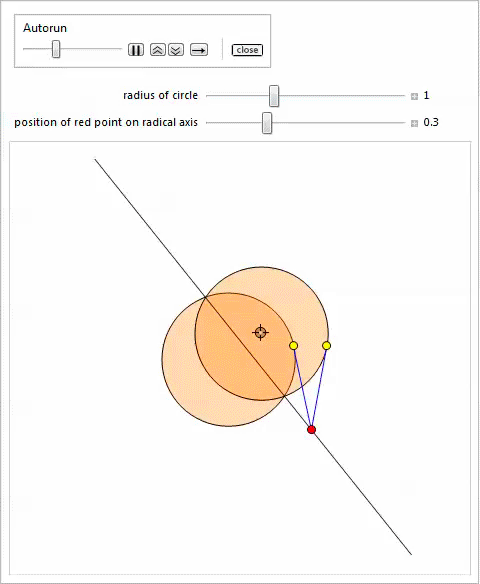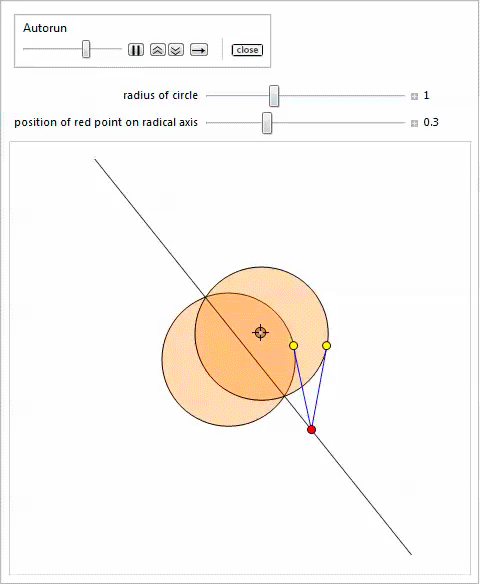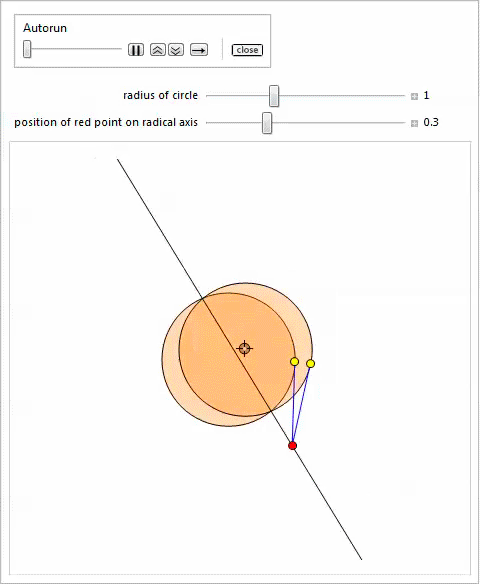
Пересечение двумерного и трехмерного арбелосов

В данной демонстрации показаны два обобщения.

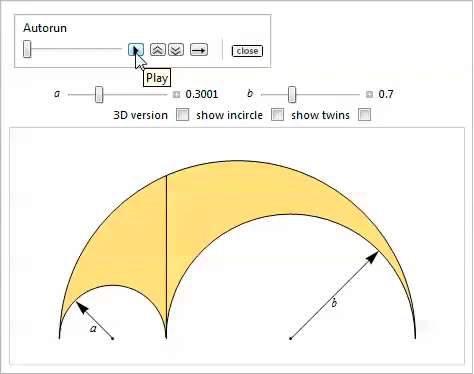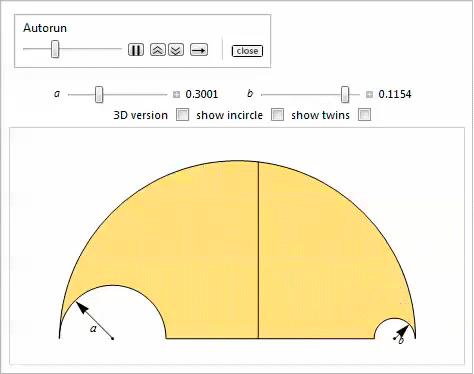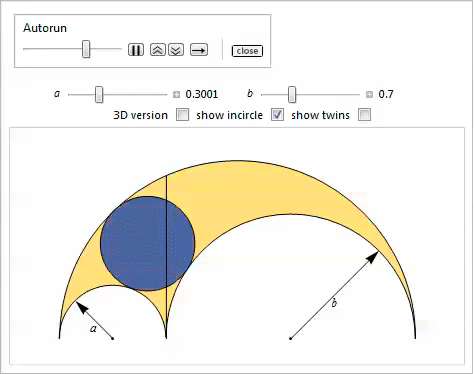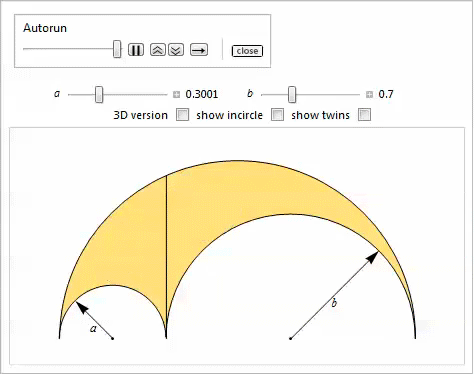
Свойство 28
Вписанные окружности касаются радикальной оси боковых и верхней дуг, и каждая из дуг в обобщённом арбелосе имеет одинаковый радиус.

Пусть — длина зазора между основаниями (то есть диаметр верхней дуги равен ) и пусть — абсцисса пересечения радикальных осей с осью , предполагая, что начало находится в крайней левой точке арбелоса [10].

Теорема 5
Если окружности и не пересекаются, то их радикальная ось пересекает отрезок в точке , так что .

Воспользовавшись данной теоремой, вычислим значение .

Не теряя обобщённости, можем предположить, что , , и ( может принимать отрицательное значение). Назовём вписанные окружности как и . Значения этих параметров получаются следующим образом.

Тогда, хоть некоторыми центрами можно и пренебречь, но радиус будет одинаков в любом случае.

Доказательство без слов

Собственно, вот еще три свойства арбелоса. Посмотрим, сможете ли Вы догадаться, какие где свойства задействованы, экспериментируя с элементами управления [24,25].

Первый Manipulate позволяет передвигать боковые дуги.

Второй Manipulate позволяет вращать прямую вокруг точки касания боковых дуг.

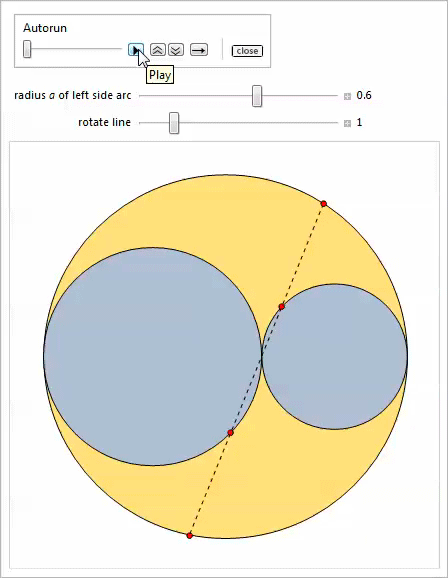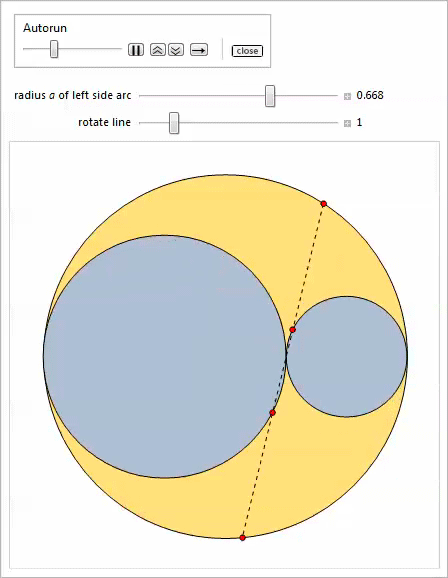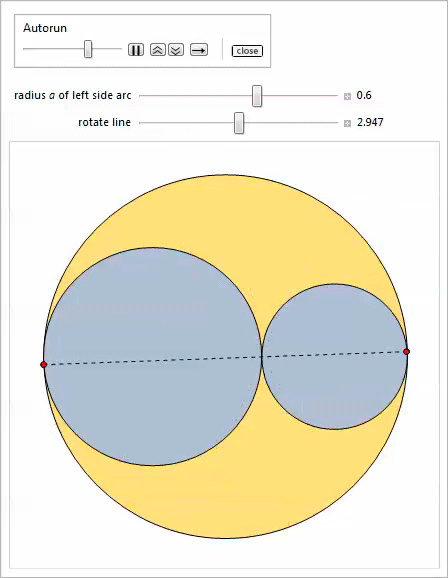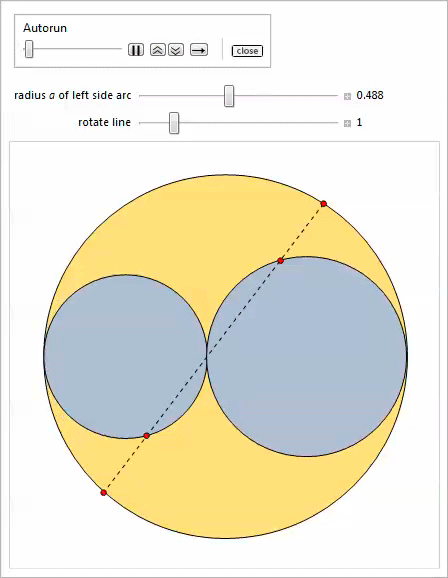
Наконец, третий Manipulate показывает бесконечное семейство близнецов.

Список литературы

[1] F. van Lamoen. “Online Catalogue of Archimedean Circles.” (Jan 22, 2014) home.planet.nl/~lamoen/wiskunde/arbelos/Catalogue.htm.

[2] S. Garcia Diethelm. “Planar Stress Rotation” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/PlanarStressRotation.

[3] C. W. Dodge, T. Schoch, P. Y. Woo, and P. Yiu, “Those Ubiquitous Archimedean Circles,” Mathematical Magazine, 72(3), 1999 pp. 202-213. www.jstor.org/stable/2690883.

[4] H. P. Boas, “Reflection on the Arbelos,” American Mathematical Monthly, 113(3), 2006 pp. 236-249.

[5] H. D. Dörrie, 100 Great Problems of Elementary Mathematics: Their History and Solution (D. Antin, trans.), New York: Dover Publications, 1965.

[6] J. Rangel-Mondragón. “Recursive Exercises II: A Paradox” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/RecursiveExercisesIIAParadox.

[7] R. B. Nelsen, “Proof without Words: The Area of an Arbelos,” Mathematics Magazine, 75(2), 2002 p. 144.

[8] A. Gadalla. “Area of the Arbelos” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/AreaOfTheArbelos.

[9] J. Rangel-Mondragón, “Selected Themes in Computational Non-Euclidean Geometry. Part 1. Basic Properties of Inversive Geometry,” The Mathematica Journal, 2013. www.mathematica-journal.com/2013/07/selected-themes-in-computational-non-euclidean-geometry-part-1.

[10] D. Pedoe, Geometry: A Comprehensive Course, New York: Dover, 1970.

[11] M. Schreiber. “Orthogonal Circle Inversion” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/OrthogonalCircleInversion.

[12] M. G. Welch, “The Arbelos,” Master’s thesis, Department of Mathematics, University of Kansas, 1949.

[13] L. Bankoff, “The Marvelous Arbelos,” The Lighter Side of Mathematics (R. K. Guy and R. E. Woodrow, eds.), Washington, DC: Mathematical Association of America, 1994.

[14] G. L. Alexanderson, “A Conversation with Leon Bankoff,” The College Mathematics Journal, 23(2),1992 pp. 98-117.

[15] S. Kabai. “Tangent Circle and Arbelos” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/TangentCircleAndArbelos.

[16] G. Markowsky and C. Wolfram. “Theorem of the Owl’s Eyes” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/TheoremOfTheOwlsEyes.

[17] P. Y. Woo, “Simple Constructions of the Incircle of an Arbelos,” Forum Geometricorum, 1, 2001 pp. 133-136. forumgeom.fau.edu/FG2001volume1/FG200119.pdf.

[18] B. Alpert. “Archimedes’ Twin Circles in an Arbelos” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/ArchimedesTwinCirclesInAnArbelos.

[19] J. Rangel-Mondragón. “Twins of Arbelos and Circles of a Triangle” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/TwinsOfArbelosAndCirclesOfATriangle.

[20] H. Okumura, “More on Twin Circles of the Skewed Arbelos,” Forum Geometricorum, 11, 2011 pp. 139-144. forumgeom.fau.edu/FG2011volume11/FG201114.pdf.

[21] E. W. Weisstein. “Point-Line Distance—2-Dimensional” from Wolfram MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/Point-LineDistance2-Dimensional.html.

[22] L. Bankoff, “Are the Twin Circles of Archimedes Really Twins?,” Mathematics Magazine, 47(4), 1974 pp. 214-218.

[23] F. Power, “Some More Archimedean Circles in the Arbelos,” Forum Geometricorum, 5, 2005 pp. 133-134. forumgeom.fau.edu/FG2005volume5/FG200517.pdf.

[24] A. V. Akopyan, Geometry in Figures, CreateSpace Independent Publishing Platform, 2011.

[25] H. Okumura and M. Watanabe, “Characterizations of an Infinite Set of Archimedean Circles,” Forum Geometricorum, 7, 2007 pp. 121-123. forumgeom.fau.edu/FG2007volume7/FG200716.pdf.

ссылка на оригинал статьи http://habrahabr.ru/post/257319/