Хочу в очередной раз затронуть метод реализации умножения Карацубы с использованием возможностей стандарта C++11. Данный алгоритм неоднократно рассматривался здесь («Умножение длинных чисел методом Карацубы», «Алгоритм Карацубы для умножения двух чисел»), но видимо из-за того, что я не умею их готовить, первый вариант не работал с числами разной длины, а второй делает не совсем то, что было нужно.
Для тех, кто не устал от этой заезженной темы, а также всех, кто испытывает трудности с реализацией этого простого, но очень эффективного алгоритма, прошу читать дальше.
Оглавление
Введение

Всех нас учили умножать в столбик в школе. Это самый простой алгоритм, который известен уже много тысяч лет:
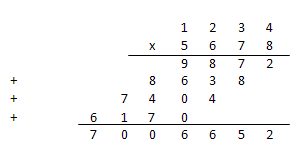
Даже Андрей Николаевич Колмогоров в 1956 году сформулировал гипотезу ![]() (которая заключалась в нижней оценке умножения величиной порядка
(которая заключалась в нижней оценке умножения величиной порядка ), так как если бы существовал какой-либо другой более быстрый алгоритм, то за такой огромный промежуток времени он был бы найден.
Псевдокод наивного умножения прост как и сам метод:
multiply(x[0 ... l], y[0 ... r]): res = [0 ... r+l] for (i = 0, i < r; ++i): carry = 0 for (j = 0, j < l; ++j): res[i + j] += carry + x[i] * y[j] carry = res[i + j] / base // base - база представления числа res[i + j] %= base res[i + l] += carry За простоту порой приходится платить производительностью, но этот алгоритм можно оптимизировать и не вычислять остаток на каждом шаге.
Через несколько лет после формулировки гипотезы Колмогорова, Анатолий Алексеевич Карацуба нашел более быстрый метод. Его подход был обобщен до парадигмы «разделяй и властвуй». Чтобы понять как это работает, рассмотрим два числа длины , которые мы разобьем на две части длины
:
Теперь заметим, что[1]:
Видно, что необходимо сделать 4 умножения и тогда сложность ничем не отличается от наивного алгоритма. Но Анатолий Алексеевич Карацуба заметил, что обойтись можно 3 умножениями чисел длины —
,
,
. Действительно:
Мы обошлись тремя умножениями вместо четырех и следовательно время работы алгоритма Карацубы удовлетворяет соотношению[2]:
,
что в итоге дает общую сложность алгоритма .
Псеводкод алгоритма умножения Карацубы:
Karatsuba_mul(X, Y): // X, Y - целые числа длины n n = max(размер X, размер Y) если n = 1: вернуть X * Y X_l = левые n/2 цифр X X_r = правые n/2 цифр X Y_l = левые n/2 цифр Y Y_r = правые n/2 цифр Y Prod1 = Karatsuba_mul(X_l, Y_l) Prod2 = Karatsuba_mul(X_r, Y_r) Prod3 = Karatsuba_mul(X_l + X_r, Y_l + Y_r) вернуть Prod1 * 10 ^ n + (Prod3 - Prod1 - Prod2) * 10 ^ (n / 2) + Prod2 И пример на небольших числах, чтобы закрепить механизм работы:
a = 12 b = 81 res = Karatsuba_mul(a, b): // размер a = размер b = 2 n = max( размер a, размер b) // n = 2 X_l = 1, X_r = 2 // 1 | 2 Y_l = 8, Y_r = 1 // 8 | 1 Prod1 = Karatsuba_mul(1, 8) // Prod1 = 8 Prod2 = Karatsuba_mul(2, 1) // Prod2 = 2 Prod3 = Karatsuba_mul(3, 9) // Prod3 = 27 вернуть 8 * 10 ^ 2 + (27 - 2 - 8) * 10 + 2 ----------------------------------------------- res = 972
Реализация
Вот мы и готовы приступить к реализации алгоритма на языке C++. В интернете я находил несколько реализаций, использующие C-стиль написания кода, что несколько затрудняет чтение его для новичков. Поэтому я решил насколько это возможно использовать улучшения доступные в стандарте C++11. Да, это замедлит код, но ведь здесь нас интересует в первую очередь простота для понимания и удобочитаемость.
- Хранение числа. Используем стандартный вектор целых чисел, с которым все, изучающие C++, знакомы. Длинное число будем читать в строку и с конца разбивать на разряды, соответствующие выбранной базе (в начале — 10).
Например, на вход получили число:
123456789000000000В нашем контейнере оно будет хранится так:
|0|1|2|3|4|5|...|n| 0 0 0 0 0 0 ... 1Код функции get_number()vector<int> get_number(istream& is) { string snum; vector<int> vnum; // индикатор разрядов unsigned int dig = 1; int n = 0; is >> snum; for (auto it = snum.crbegin(); it != snum.crend(); ++it) { n += (*it - '0') * dig; dig *= dig_size; // если разряд равен базе, то выталкиваем число в вектор if (dig == base) { vnum.push_back(n); n = 0; dig = 1; } } if (n != 0) { vnum.push_back(n); } return vnum; } - Получение числа. На вход у нас могут поступать числа разной длины и нам для успешной работы алгоритма желательно привести к одной и той же длине, кратной 2 (так как мы постоянно разбиваем наши «длинные» числа пополам). Напишем функцию extend_vec(), которая брала бы наш вектор и удлиняла его как-то так:
first = {4}; // 4; size = 1 second = {3, 2, 1} // 123; size = 3 int n = max(first.size(), second.size()); extend_vec(first, n); // добавить 3 нуля extend_vec(second, n); // добавить 1 нольКод функции extend_vec()void extend_vec(vector<int>& v, int len) { // Увеличиваем len до кратности степени двойки while (len & (len - 1)) { ++len; } len -= v.size(); while (len--) { v.push_back(0); } } - Умножение. Здесь стоит поговорить о нескольких оптимизациях, которые стоит сделать. Мы не будем считать остатки и переносить их в старшие разряда на каждом рекурсивном вызове, а сделаем это в конце. И для перемножения двух чисел с длинной меньше, скажем, 128 будем использовать наивный алгоритм, так как он является меньшей константой, чем алгоритм Карацубы.
Код функции naive_mul()
vector<int> naive_mul(const vector<int>& x, const vector<int>& y) { int len = x.size(); vector<int> res(2 * len); for (int i = 0; i < len; ++i) { for (int j = 0; j < len; ++j) { res[i + j] += x[i] * y[j]; } } return res; }Код функции karatsuba_mul()vector<int> karatsuba_mul(const vector<int>& x, const vector<int>& y) { int len = x.size(); vector<int> res(2 * len); if (len <= len_f_naive) { return naive_mul(x, y); } int k = len / 2; // Отделяем левую и правую часть числа vector<int> Xr {x.begin(), x.begin() + k}; vector<int> Xl {x.begin() + k, x.end()}; vector<int> Yr {y.begin(), y.begin() + k}; vector<int> Yl {y.begin() + k, y.end()}; vector<int> P1 = karatsuba_mul(Xl, Yl); vector<int> P2 = karatsuba_mul(Xr, Yr); // Считаем сумму Xl + Xr и Yl + Yr vector<int> Xlr(k); vector<int> Ylr(k); for (int i = 0; i < k; ++i) { Xlr[i] = Xl[i] + Xr[i]; Ylr[i] = Yl[i] + Yr[i]; } vector<int> P3 = karatsuba_mul(Xlr, Ylr); // Считаем P3 - P1 - P2 for (int i = 0; i < len; ++i) { P3[i] -= P2[i] + P1[i]; } // Формируем результат // P2 - младшая часть for (int i = 0; i < len; ++i) { res[i] = P2[i]; } // P1 - старшая часть for (int i = len; i < 2 * len; ++i) { res[i] = P1[i - len]; } // P3 - P1 - P2 добавляем в середину нашего числа for (int i = k; i < len + k; ++i) { res[i] += P3[i - k]; } return res; } - Нормализация. Осталось сделать все переносы и можно выводить результат (или использовать для дальнейших вычислений).
Код функции finalize()
void finalize(vector<int>& res) { for (int i = 0; i < res.size(); ++i) { res[i + 1] += res[i] / base; res[i] %= base; } }И выводим результат, дополняя нулями при использование базы, большей, чем 10.
Код функции print_res()void print_res(const vector<int>& v, ostream& os) { auto it = v.crbegin(); // Passing leading zeroes while (!*it) { ++it; } while (it != v.crend()) { int z = -1; int num = *it; if (num == 0) { num += 1; } if (num < add_zero) { z = 1; while ((num *= dig_size) < add_zero) { ++z; } } if (z > 0) { while (z--) { os << '0'; } } os << *it++; } os << endl; }
Сравнение скорости работы наивного алгоритма и алгоритма Карацубы
Для сборки тестовой программы использовался Clang++ с ключом -O3. Результаты тестирования для представления чисел с базой 10 приведены на рисунке 1.
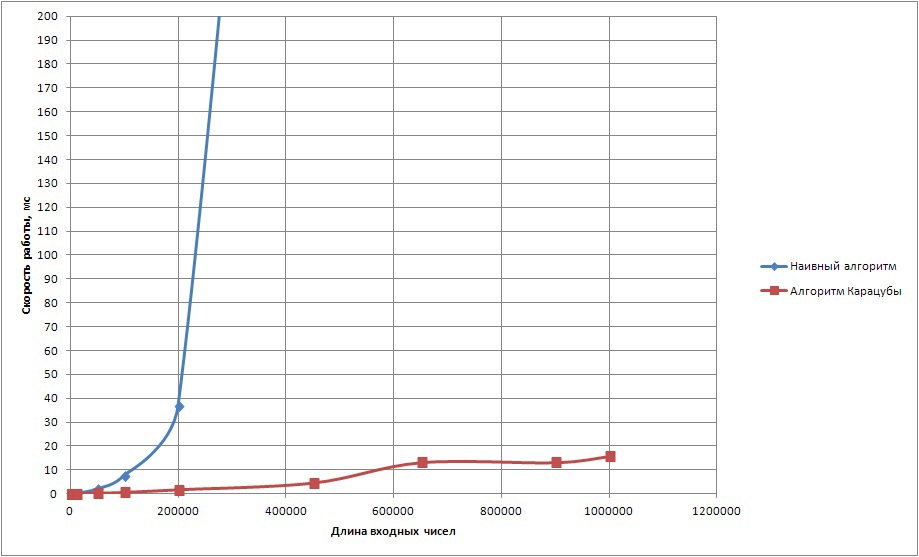
Рисунок 1. Время расчета произведения двух чисел, используя представление с базой 10
Видно, что наивный алгоритм ощутимо замедляется при входных числах, длина которых больше .
На рисунке 2 показан результат работы тех же алгоритмов, но с небольшой оптимизацией. Теперь длинное число помещается в вектор с использованием базы 100, что дает существенный прирост в производительности.
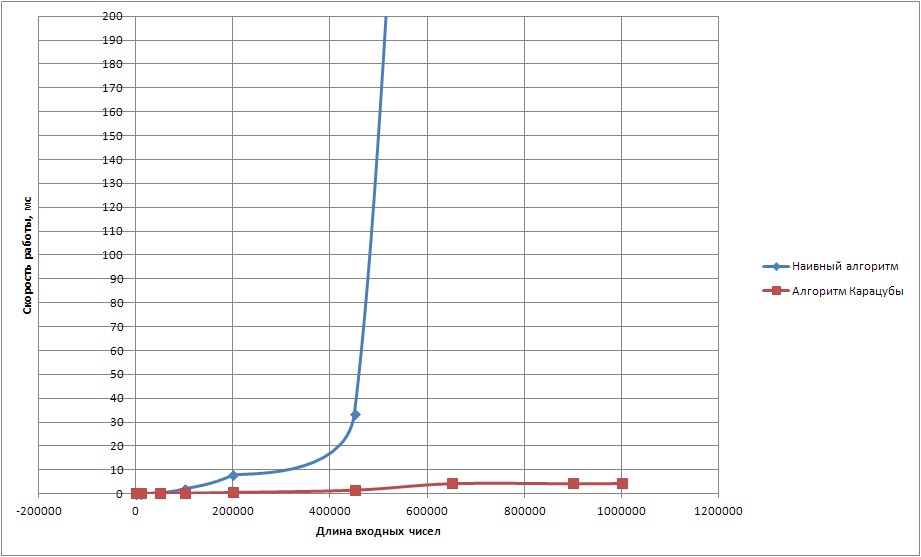
Рисунок 2. Время расчета произведения двух чисел, используя представление с базой 100
Выводы
Вот и все, мы разобрали с вам этот простой и эффективный способ умножения. Надеюсь, это материал будет полезен и многие новички, которые только начинают изучение алгоритмов не будут больше впадать в ступор (ну не зашел он у меня с первого раза в свое время).
Ещё есть куда оптимизировать данную реализацию:
- увеличить базу в которой хранятся числа в векторе. Сейчас нормализация числа делается в самом конце, что вызывает переполнение стандартных типов в C++. Возможно стоит хранить числа в массиве/векторе типа unsigned long long и вычислять остатки с переносами на каждом этапе умножения. Либо использовать «длинное» представление остатка.
- отказаться от векторов в пользу массивов и не использовать выделение левой и правой части числа с помощью итераторов.
На этом все, всем спасибо за внимание.
Исходный проект, который использовался при написании статьи, находится здесь.
Список используемой литературы
- С. Дасгупта Алгоритмы: Перевод с английского А. С. Куликова под редакцией А. Шеня [Текст] / С. Дасгупта, Х. Пападимитриу, У. Вазирани. -Москва: МЦНМО, 2014 — 320 с.
- Karatsuba algorithm [Электронный ресурс] / Wikipedia — URL: en.wikipedia.org/wiki/Karatsuba_algorithm
- А. С. Куликов Алгоритмы и структуры данных [Электронный ресурс] / А. С. Куликов — URL: https://stepic.org/course/Алгоритмы-и-структуры-данных-63/syllabus
ссылка на оригинал статьи http://habrahabr.ru/post/262705/
Добавить комментарий