Работа посвящена погрешностям округления, возникающим при вычислениях у чисел с плавающей запятой. Здесь будут кратко рассмотрены следующие темы: «Представление вещественных чисел», «Способы нахождения погрешностей округления у чисел с плавающей запятой» и будет приведен пример компенсации погрешностей округления.
В данной работе примеры приведены на языке програмиирования C.
Представление вещественных чисел
Рассмотрим представление конечного действительного числа в стандарте IEEE 754-2008 в виде выражения, которое характеризуется тремя элеменами: S (0 или 1), мантисса M и порядок E:
v = -1S * b(E — BIAS) * M
- основанием b (стандартом определено три двоичных формата и два десятичных);
- длиной мантиссы p, определяющей точность представления числа, измеряется в цифрах (двоичных или десятичных);
- максимальным значением порядка emax;
- минимальным значением порядка emin; стандарт требует, чтобы выполнялось условие:
emin = 1-emax - BIAS (смещение); порядок записывается в т. н. смещенной форме, т. е.
реальное значение показателя степени равно E-BIAS.
Ниже в таблице даны параметры стандартных форматов чисел с плавающей запятой. Здесь: w — ширина битового поля для представления порядка, t — ширина битового поля для представления мантиссы, k — полная ширина битовой строки.

В следующией таблице представлены диапазоны изменения и точность стандартных 32 и 64-х разрядных форматов вещественных чисел с плавающей запятой.
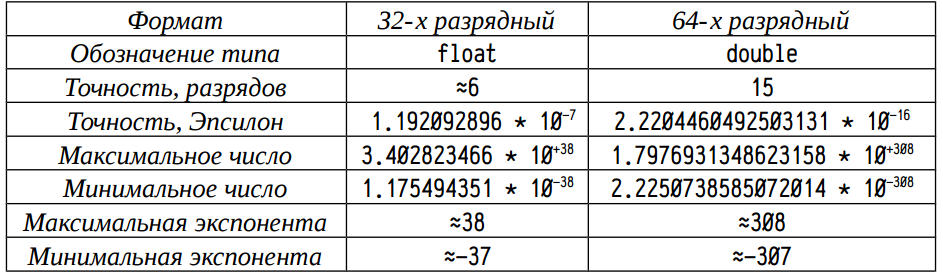
Здесь «Точноть, Эпсилон» — наименьшее число, для которого истинно выражение:
1 + EPSILON != 1Данная величина «Эпсилон», характеризует относительную точность операций сложения и вычитания: если прибавляемая к x или вычитаемая из x величина меньше, чем epsilon*x, то результат останется равен x. На практике, в ряде случаев, при использовании в аддитивных операциях величин, приближающихся по порядку к epsilon*x, начинают сказываться погрешности округления меньшего слагаемого. О таких ситуациях и пойдет речь в данной работе.
Рассмотрим представление вещественного числа для типа данных float(Binary32).

В данном примере:
- Число V = 0,1562510
- Знак S = 0, т.е. +
- Порядок (E — BIAS) = 011111002 — 011111112 = 12410 — 12710 = -310
- Мантисса M = 1,010000000000000000000002
Таким образом, число V = 1,012*210-310 = 1012*210-510 = 510*210-510 = 0,1562510
Заметим, что при выполнении операций с вещественными числами часто результат не будет помещаться в N-разрядные матиссы, т.е. будет происходить округление. Округление в одной вычислительной операции не превывает порядок EPSILON/2, но когда нам требуется делать много операций, то для повышения точности вычисления результата нам надо научиться находить, насколько именно результат каждой конкретной операции округлён.
Более подробно про округления и нарушение аксиоматики рассказано в файле makarov_float.pdf (ссылка на материал внизу).
Способы нахождения погрешностей округления у чисел с плавающей запятой
Данную проблему исследовали многие специалисты, наиболее известными из них являются: Дэвид Голдберг, Уильям Кэхен, Джонатан Ричард Шевчук.
Ниже мы рассмотрим алгоримы нахождения погрешностей округления, приведенные в работе Шевчука, на примере двух функций:
- TwoSum — функция нахождения погрешности округления при сложении.
- TwoProduct — функция нахождения погрешности округления при умножении.
Для правильного понимания указанных алгоритмов мы будем опираться на теоремы, которые рассмотрены в работе Шевчука. Теоремы приводим без доказательств.
Говоря, что число a является p-битовым числом, имеется ввиду, что длина матиссы числа a представляется p битами.
TwoSum
Теорема: пусть числа a и b являются p-битовыми числами с плавающей запятой, где p >= 3, тогда следуя данному алгоритму мы получим 2 числа: x и y, для которых выполняется условие: a + b = x + y. Причем x является апроксиммацией суммы a и b, а y является погрешностью округления вычисления числа x.

TwoProduct
В действительности, алогритм находжения погрешности огругления при умножении двух вещественных чисел состоит из 2-х функций: Split — вспомогательной функции и функции TwoProduct, где мы находим погрешность.
Рассмотрим алгоритм функции Split.
Split
Теорема: число a — p-битовое число с плавающей запятой, где p >= 3. Выберем точку разрыва s, где p/2 <= s <= p-1. Следуя алгоритму, получим (p — s)-битное число — число a_hi и (s-1)-битное число — a_lo, где |a_hi| >= |a_low| и a = a_hi + a_low.

Теперь перейдем к анализу функции TwoProduct.
TwoProduct
Теорема: пусть числа a и b являются p-битовыми числами с плавающей запятой, где p >= 6. Тогда, выполняя данный алгоритм, мы получим 2 числа: x и y, для которых выполняется условие: a*b = x + y. Причем x является апроксиммацией произведения чисел a и b, а число y является погрешностью округления вычисления числа x.

Видно, что конечный результат представляется парой N-битовых вещественных чисел: результат + погрешность. Причем второе должно иметь порядок не более EPSILON по отношению к первому.
Пример компесации погрешностей округления у чисел с плавающей запятой
Теперь перейдем к практическим расчетам, которые построены на алгоритмах Шевчука. Найдем погрешности округления при сложении и умножении чисел с плавающей запятой и проанализируем, как накапливается погрешность.
Погрешность округления суммы
Приведем пример простейшей программы суммирования:
#include <stdio.h> #include <math.h> int main() { float val = 2.7892; printf("%0.7g \n", val); val = val/10000000000.0; float result = 0.0; for (long long i = 0; i < 10000000000; i++) { result += val; } printf("%0.7g \n", result); return 0; } В результате работы программы, мы должны получить два одинаковых числа: 2,7892 и 2,7892. Но в консоль было выведено: 2,7892 и 0,0078125. Отсюда видно, что погрешность накопилась очень большая.
Теперь попробуем сделать то же самое, но, используя алгоритм Шевчука, будем накапливать погрешность в отдельную переменную, а затем скомпенсируем результат путем прибавления ошибки к главной переменной суммы.
#include <stdio.h> #include <math.h> float TwoSum(float a, float b, float& error) { float x = a + b; float b_virt = x - a; float a_virt = x - b_virt; float b_roundoff = b - b_virt; float a_roudnoff = a - a_virt; float y = a_roudnoff + b_roundoff; error += y; return x; } int main() { float val = 2.7892; printf("%0.7g \n", val); val = val/10000000000.0; float result = 0.0; float error = 0.0; for (long long i = 0; i < 10000000000; i++) { result = TwoSum(result, val, error); } result += error; printf("%0.7g \n", result); return 0; } В итоге мы получаем 2 числа: 2,7892 и 0,015625. Результат улучшился, но погрешность все равно дает о себе знать. В данном примере не была учтена погрешость, возникающая в операции сложения, в функции TwoSum():
error += y; Будем компенсировать результат на каждой итерации цикла и перезаписывать ошибку в переменную, которая накапливает погрешность округления в операции суммирования. Для этого модифицируем функцию TwoSum(): добавим переменную isNull типа bool которая указывает на то, стоит ли нам накапливать погрешность или же стоит ее перезаписать.
В итоге, result будет представляться 2 переменными: result — главная переменная, error1 — погрешность операции result += val.
Код будет выглядеть следующим образом:
#include <stdio.h> #include <math.h> float TwoSum(float a, float b, float& error, bool isNull) { float x = a + b; float b_virt = x - a; float a_virt = x - b_virt; float b_roundoff = b - b_virt; float a_roudnoff = a - a_virt; float y = a_roudnoff + b_roundoff; if (isNull) { error = y; } else { error += y; } return x; } int main() { float val = 2.7892; printf("%0.7g \n", val); val = val/10000000000.0; float result = 0.0; float error1 = 0.0; for (long long i = 0; i < 10000000000; i++) { result = TwoSum(result, val, error1, false); result = TwoSum(error1, result, error1, true); } printf("%0.7g \n", result); return 0; } Программа выведет числа: 2,7892 и 2,789195.
Заметим, что здесь не была учтена погрешность округления, возникающая в операции умножения:
val = val*(1/10000000000.0); Учтем эту погрешность путем добавления функций учета погрешностей умножения, которые разработал Д.Р. Шевчук. При этом переменная val будет представлена двумя переменными:
val_real = val + errorMult Таким образом, result будет представляться 3 переменными: result — главная переменная, error1 — погрешность операции result += val, error2 — погрешность операции result += errorMult.
Так же мы будем складывать переменные error1 и error2, а погрешность от этой операции записывать в error2.
В итоге, код:
#include <stdio.h> #include <math.h> float TwoSum(float a, float b, float& error, bool isNull) { //isNull отвечает за то, стоит ли нам накопить возникающую погрешность // или же стоит перепизаписать ее float x = a + b; float b_virt = x - a; float a_virt = x - b_virt; float b_roundoff = b - b_virt; float a_roudnoff = a - a_virt; float y = a_roudnoff + b_roundoff; if (isNull) { error = y; } else { error += y; } return x; } void Split(float a, int s, float& a_hi, float& a_lo) { float c = (pow(2, s) + 1)*a; float a_big = c - a; a_hi = c - a_big; a_lo = a - a_hi; } float TwoProduct(float a, float b, float& err) { float x = a*b; float a_hi, a_low, b_hi, b_low; Split(a, 12, a_hi, a_low); Split(b, 12, b_hi, b_low); float err1, err2, err3; err1 = x - (a_hi*b_hi); err2 = err1 - (a_low*b_hi); err3 = err2 - (a_hi*b_low); err += ((a_low * b_low) - err3); return x; } int main() { float val = 2.7892; printf("%0.7g \n", val); float errorMult = 0;//погрешность умножения val = TwoProduct(val, 1.0/10000000000.0, errorMult); float result = 0.0; float error1 = 0.0; float error2 = 0.0; for (long long i = 0; i < 10000000000; i++) { result = TwoSum(result, val, error1, false); result = TwoSum(result, errorMult, error2, false); error1 = TwoSum(error2, error1, error2, true); result = TwoSum(error1, result, error1, true); } printf("%0.7g \n", result); return 0; } В консоль были выведены следующие числа: 2,7892 и 2,789195.
Это говорит о том, что погрешность округления умножения достаточно мала, чтоб проявиться даже на 10 миллиардах итераций. Данный результат является максимально приближенным к исходному числу, если учитывать погрешности в операциях сложения и умножения. Для получение более точного результата можно ввести дополнительные переменные, учитывающие погрешности. Скажем, добавить переменную, учитывающую погрешность в операции накопления основной погрешности в функции TwoSum(). Тогда эта погрешность будет иметь порядок EPSILON2, по отношению к главному результату (первая погрешность будет иметь порядок EPSILON).
Погрешность округления умножения
Посчитаем число 1.0012101 в цикле, т.е. сделаем следующие:
#include <stdio.h> #include <math.h> int main() { float val = 1.0012; float result = 1.0012; for (long long i = 0; i < 100; i++) { result *= val; } printf("%0.15g \n", result); return 0; } Заметим, что точный результат, с точностью до пятнадцатого знака после запятой, равен 1.128768638496750. Мы получим: 1.12876391410828. Как видно, погрешность оказалось достаточно большой.
Выведем переменную val, приведя ее к типу данных double, и посмотрим, что в нее на самом деле записалось:
printf("%0.15g \n", (double)val); Мы получим число 1.00119996070862. Это говорит о том, что в программировании даже самая точная константа не является ни надежной, ни константой. Поэтому, наш реальный точный результат будет равен 1.128764164435784, с точностью до пятнадцатого знака после запятой.
Теперь попробуем улучшить полученный ранее результат. Для этого введем компенсацию результата вычислений, путем учета погрешности округления в операции умножения. Так же будем пытаться прибавлять накопившуюся погрешность к переменной result на каждом шаге.
Код:
#include <stdio.h> #include <math.h> float TwoSum(float a, float b, float& error, bool isNull) { //isNull отвечает за то, стоит ли нам накопить возникающую погрешность // или же стоит перепизаписать ее float x = a + b; float b_virt = x - a; float a_virt = x - b_virt; float b_roundoff = b - b_virt; float a_roudnoff = a - a_virt; float y = a_roudnoff + b_roundoff; if (isNull) { error = y; } else { error += y; } return x; } void Split(float a, int s, float& a_hi, float& a_lo) { float c = (pow(2, s) + 1)*a; float a_big = c - a; a_hi = c - a_big; a_lo = a - a_hi; } float TwoProduct(float a, float b, float& err) { float x = a*b; float a_hi, a_low, b_hi, b_low; Split(a, 12, a_hi, a_low); Split(b, 12, b_hi, b_low); float err1, err2, err3; err1 = x - (a_hi*b_hi); err2 = err1 - (a_low*b_hi); err3 = err2 - (a_hi*b_low); err += ((a_low * b_low) - err3); return x; } int main() { float val = 1.0012; float result = 1.0012; float errorMain = 0.0; for (long long i = 0; i < 100; i++) { result = TwoProduct(result, val, errorMain); result = TwoSum(errorMain, result, errorMain, true); } printf("%0.15g \n", result); return 0; } Программа выводит следующее число: 1.12876415252686. Мы получили погрешность 1.0e-008, что меньше чем EPSILON/2 для типа данных float. Таким образом, данный результат можно считать достаточно хорошим.
Итоги
1) В данной работе было рассмотрено представление чисел с плавающей запятой в формате стандарта IEEE 754-2008.
2) Был показан способ нахождения погрешностей округления в операциях сложения и умножения у чисел с плавающей запятой.
3) Были рассмотрены простые примеры компенсации погрешностей округления у чисел с плавающей запятой.
Работу выполнил Виктор Фадеев.
Консультировал Макаров А.В.
P.S. Спасибо за найденные ошибки пользователям:
xeioex, Albom.
Использованная литература
- Работы Макарова Андрея Владимировича на тему «Представление вещественных чисел». В файле makarov_float .pdf показано, как возникают погрешности округления у чисел с плавающей запятой.
- Википедия. Число одинарной точности.
- Adaptive Precision Floating-Point Arithmetic
and Fast Robust Geometric Predicates
Jonathan Richard Shewchuk
ссылка на оригинал статьи http://habrahabr.ru/post/266023/
Добавить комментарий