Алгоритм шифрования RC5 и его реализация на python

Алгоритм RC5

В своём посте, я хотел бы рассказать о симметричном алгоритме шифрования RC5 и моей версии его реализации на python. Данный алгоритм разработан известнейшим криптологом Рональдом Макдональдом Ривестом — одним из разработчиков системы RSA и основателей одноименной фирмы. По количеству пользователей RC5 стоит в одном ряду с такими известными алгоритмами как IDEA и Blowfish. Аббревиатура RC обозначает, по разным источникам, либо Rivest Cipher, либо Ron’s Code, что в совокупности даёт нам «шифр Рона Ривеста». Заинтересовавшихся прошу под кат.

Введение

При описании алгоритма будем использовать следующие обозначения:

• Размер слова 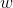в битах. RC5 шифрует блоками по два слова; допустимыми значениями являются 16, 32 и 64. Данную величину рекомендуется брать равной машинному слову. Например для 32-битных машин 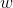= 32 и следовательно размер блока будет равен 64 бита
• Количество раундов алгоритма 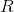— целое число от 0 до 255 включительно. При значении 0 шифрование выполняться не будет
• Размер секретного ключа 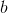в байтах — целое число от 0 до 255 включительно

Для уточнения параметров, используемых в конкретном случае применяется обозначение RC5-;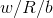
например, RC5-32/12/16 обозначает алгоритм RC5 c 64-битным блоком, 12 раундами шифрования и 16-байтным ключом(данная комбинация рекомендуется Ривестом в качестве основного варианта).

Работа алгоритма состоит из двух этапов:

• Процедура расширения ключа
• Само шифрование

Создадим класс и конструктор инициализирующий необходимые стартовые переменные

class RC5:     def __init__(self, W, R, key):         self.W = W         self.R = R         self.key = key 

Процедура расширения ключа

Предлагаю начать с этапа, который немного сложней, а именно, с процедуры расширения ключа. Для этого нам понадобится написать 3 простеньких функции:

• Выравнивания ключа
• Инициализации массива расширенных ключей
• Перемешивания массивов ключей

Выравнивание ключа

Если размер ключа(в байтах) не кратен 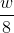, дополняем его нулевыми байтами до ближайшего размера кратного 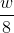. После этого ключ копируется в массив , где 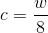. Проще говоря, мы копируем ключ блоками по 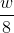байт (2, 4, 8 для значений 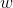16, 32, 64 соответственно) в массив .
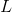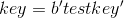Например, при параметрах и значении ключа мы получим и (под 0 подразумевается нулевой байт).

Опишем необходимую функцию

def __keyAlign(self):     while len(self.key) % (self.W // 8): # дополняем ключ байтами \x00         self.key += b'\x00'     self.c = len(self.key) // (self.W // 8)     L, key = [], bin(int.from_bytes(self.key, byteorder='little'))[2:] # функция from_bytes преобразует массив байт в число     for i in range(self.c): # Заполняем массив L         L.append(int(key[:self.W], 2))         key = key[self.W:]     self.L = L 

Инициализация массива расширенных ключей

На этом шаге нам нужно сгенерировать псевдослучайные константы 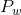и 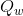по следующим формулам:

,
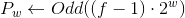
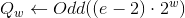где
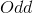— функция округления до ближайшего нечентного
— экспонента
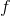— золотое сечение

Так же в спецификации алгоритма приведены уже вычисленные константы для всех возможных значений :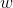





,
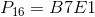
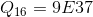
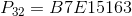
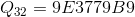
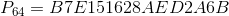
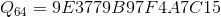все константы представлены в шестнадцатеричном виде.

Получив всё необходимое мы инициализируем массив , где

Описание функций

    def __const(self): # функция генерации констант         if self.W == 16:             return (0xB7E1, 0x9E37) # Возвращает значения P и Q соответсвенно         elif self.W == 32:             return (0xB7E15163, 0x9E3779B9)         elif self.W == 64:             return (0xB7E151628AED2A6B, 0x9E3779B97F4A7C15)       def __keyExtend(self): # заполнение массива S         P, Q = self.__const()         self.S = [(P + i * Q) % 2 ** self.W for i in range(2 * self.R + 1)] 

Перемешивание

Теперь, перед тем как приступить к шифрованию, нам осталось лишь перемешать элементы массивов L и S выполнив следующий цикл:



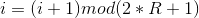
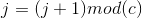, где
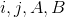— временные переменные, начальные значения равны 0
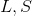— массивы полученные на предыдущих шагах
Количество итераций 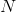определяется как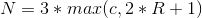

def __shuffle(self):     m = max(self.c, 2 * self.R + 1)     i, j, A, B = 0, 0, 0, 0     for k in range(3 * m):         A = self.S[i] = self.__lshift((self.S[i] + A + B), 3)         B = self.L[j] = self.__lshift((self.L[j] + A + B), A + B)         i = (i + 1) % (2 * self.R + 1)         j = (j + 1) % self.c 

Структура алгоритма

Шифрование

Алгоритм представляет собой сеть Фейстеля, в каждом раунде которой(за исключением нулевого) выполняются следующие операции:

,
где
— номер текущего раунда, начиная с 1
— фрагмент расширенного ключа
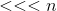— операция циклического сдвига на 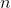битов влево

В нулевом раунде выполняется операции наложения двух первых фрагментов расширенного ключа на шифруемые данные:

Стоит отметить, что под раундом подразумевается преобразования, соответствующее двум раундам обычных алгоритмов, сконструированных на основе сетей Фейстеля. За раунд RC5 обрабатывает блок целиком, в отличии от раунда сети Фейстеля обрабатывающего один подблок — чаще всего половину блока.

Соответствующий код:

def encrypt(self, inpFileName, outFileName): # в качестве параметров передаётся имя файла и открытым текстом и имя выходного файла     with open(inpFileName, 'rb') as inp, open(outFileName, 'wb') as out: # получаем объекты файлов для чтения и записи         while True:             text = inp.read(self.W // 4) # считываем необходимое кол-во байт             if not text: # выходим из цикла, если считали пустую строку(массив байт)                  break             text = text.ljust(self.W // 4, b'\x00') # последняя считанная строка может быть меньше необходимого размера, что критичного для блочного шифра, поэтому мы дополняем её нулевыми байтами             A = int.from_bytes(text[:self.W // 8], byteorder='little')             B = int.from_bytes(text[self.W // 8:], byteorder='little')             A = (A + self.S[0]) % 2 ** self.W # нулевой раунд             B = (B + self.S[1]) % 2 ** self.W             for i in range(1, self.R):                  A = (self.__lshift((A ^ B), B)                      + self.S[2 * i]) % 2 ** self.W                 B = (self.__lshift((A ^ B), A)                      + self.S[2 * i + 1]) % 2 ** self.W             out.write(A.to_bytes(self.W // 8, byteorder='little') +                      B.to_bytes(self.W // 8, byteorder='little')) # запись зашифрованных данных в выходной файл 

Расшифровывание

Расшифровка данных выполняется применением обратных операций в обратной последовательности, т.е. сначала выполняем следующий цикл:

,
где
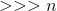— операция циклического сдвига вправо
— номер раунда в обратном порядке, т.е. начиная с 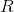и заканчивая единицей.

После этого выполняются операции обратные для нулевого раунда, а именно:

Код тут:

def decrypt(self, inpFileName, outFileName):     with open(inpFileName, 'rb') as inp, open(outFileName, 'wb') as out:         while True:             text = inp.read(self.W // 4)             if not text:                 break             A = int.from_bytes(text[:self.W // 8], byteorder='little')             B = int.from_bytes(text[self.W // 8:], byteorder='little')             for i in range(self.R - 1, 0, -1):                 B = self.__rshift(                     ((B - self.S[2 * i + 1]) % 2 ** self.W), A) ^ A                 A = self.__rshift(                     ((A - self.S[2 * i]) % 2 ** self.W), B) ^ B             B = (B - self.S[1]) % 2 ** self.W             A = (A - self.S[0]) % 2 ** self.W             res = (A.to_bytes(self.W // 8, byteorder='little')                    + B.to_bytes(self.W // 8, byteorder='little'))             out.write(res.rstrip(b'\x00')) # убираем добавленные на этапе шифрования нулевые байты 

Алгоритм поразительно прост — в нем используются только операции сложения по модулю 2 и по модулю 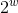, а также сдвиги на переменное число битов. Последняя из операций представляется автором алгоритма как революционное решение, не использованное в более ранних алгоритмах шифрования (до алгоритма RC5 такие использовались только в алгоритме Madryga, не получившем широкого распространения), — сдвиг на переменное число битов является весьма просто реализуемой операцией, которая, однако, существенно усложняет дифференциальный и линейный криптоанализ алгоритма. Простота алгоритма может рассматриваться как его важное достоинство — простой алгоритм легче реализовать и легче анализировать на предмет возможных уязвимостей.

Код целиком можно посмотреть на github.

Немного криптоанализа

• Существует класс ключей при использовании которых алгоритм можно вскрыть линейным криптоанализом. В других случаях это почти невозможно.
• Дифференциальный криптоанализ более эффективен при атаке на данный алгоритм. Например, для алгорима RC5-32-12-16, в лучшем случае, требуется 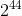выбранных открытых текстов для успешной атаки. При использовании 18-20(и больше) раундов вместо 12 вскрыть алгоритм с помощью дифференциального криптоанализа почти невозможно.

Таким образом, наиболее реальным методом взлома алгоритма RC5 (не считая варианты с небольшим количеством раундов и с коротким ключом) является полный перебор возможных вариантов ключа шифрования. Что означает, что у алгоритма RC5 практически отсутствуют недостатки с точки зрения его стойкости. На этом и хотелось бы закончить. Всем спасибо за внимание.

ссылка на оригинал статьи http://habrahabr.ru/post/267295/