
Перевод поста Peter Barendse "Surfaces and Solids of Revolution: Using Wolfram|Alpha’s «Virtual Potter’s Wheel»".
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации
Ещё до появления современной технологии 3D печати у нас была возможность создавать объекты практически любой формы, и единственные ограничения для человечества были связаны лишь с точностью, которую мы можем обеспечить. И на пути преодоления этих ограничений были разработаны разнообразные устройства, способные производить изделия очень сложных форм; кульминацией этого процесса (до появления 3D принтеров) стало появление станков с ЧПУ и большим количеством степеней свободы:
Исторически одним из первых подобных устройств, был, пожалуй, гончарный круг, с помощью которого у нас появилась возможность создавать весьма точные осесимметричные изделия произвольного профиля. Я до сих пор воспринимаю это как волшебство, смотря на то, как гончар формирует кривую своими руками; то, как эта кривая задаёт форму для всей вазы через вращение колеса:

Простым обобщением гончарного круга является токарный станок. По сути это гончарный круг для дерева или металла. Токарные станки похожи на гончарные колеса, однако заготовка располагается горизонтально, а кривую формирует некоторый острый режущий инструмент. Режущий инструмент также может быть прикреплен к направляющей с некоторым контуром, в результате чего можно производить изделия одинаковой формы.
Станок и гончарный круг могут производить определённый класс тел, которые называются телами вращения. Поверхность тела вращения есть поверхность вращения.
С точки зрения математики поверхность вращения есть результат вращения некоторой кривой, заданной на плоскости, вокруг оси (ось должна лежать на той же плоскости). Полученная поверхность вращения располагается в трехмерном пространстве. Тело вращения есть результат вращения некоторой двумерной области вокруг оси.
Поверхности и тела вращения обычно изучают на втором семестре курса математического анализа – как одну из сфер применения интегрирования. Помню, эта тема показалась мне весьма полезным учебным материалом, ведь это следующий наиболее интуитивный пример концепции интегрирования после площади под графиком, в котором, правда, используется одиночный интеграл.
Вместе с 3D-печатью и Wolfram Language студенты имеют возможность добавить визуальное представление и опыт проектирования к теории и математической интуиции, которые они уже имеют. И, как будет показано далее, совсем не обязательно что-то знать из области программирования или уметь производить расчёты для того, чтобы использовать «виртуальный гончарный круг» в Wolfram|Alpha! И, повинуясь зову гончарного круга, давайте сделаем какую-нибудь чашку!
После некоторого изучения различных функций в Wolfram|Alpha (ладно, признаюсь, тут я использовал Wolfram Language, чтобы иметь возможность интерактивного управления формой кривой) я нашёл интересную кандидатуру на роль кривой для нашей чашки – из неё должно получиться нечто вроде коктейльного бокала:
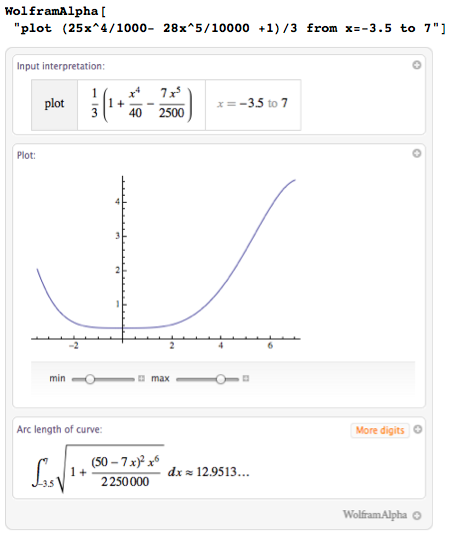
Теперь, я могу просто поменять plot (построить) на revolve (провращать), а Wolfram|Alpha расскажет мне о моём бокале и покажет его изображение:
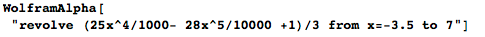
В дополнение к уравнениям, которые определяют тело и поверхность, я получаю значение объёма внутри тела и площадь его поверхности. Объем около 120 – это означает, что если в качестве единицы измерения мы использовали сантиметры, то мой бокал будет вмещать в себя 120 мл (120 куб.см).
Однако этот объем включает в себя и то, что заключено в ножке бокала и в его основании. Часть этого пространства необходимо зарезервировать для стекла (или другого материала, из которого будет изготовлен бокал). Потому давайте добавим внутреннюю кривую – я её задал путем смещения исходной кривой на 1/6 вниз и взятия её на промежутке от 3 до 7:
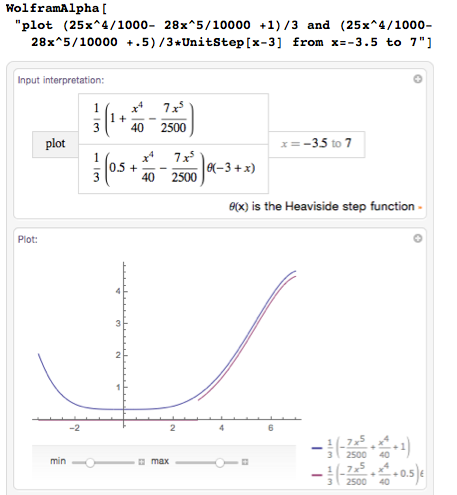
Теперь я мог бы либо распечатать этот график для использования его в качестве шаблона на своем токарном станке (если бы у меня такой был), либо продолжить работать с «виртуальным гончарным колесом»:
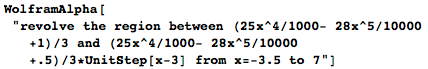
Теперь я знаю, сколько материала мне потребуется для производства одного бокала – около 20 куб.см., то есть у нас остаётся около 100 мл пространства для размещаемого в бокале питья. Можно также вычислить то, сколько краски нам нужно потратить для окрашивания бокала. Площадь его поверхности составляет приблизительно 233 см², а на банках с краской обычно указывается то, на покраску какой площади её хватит.
Чтобы распечатать эту чашу через сайт Shapeways, я воспользовался упрощенным способом, о котором в прошлом году писал Виталий Кауров.
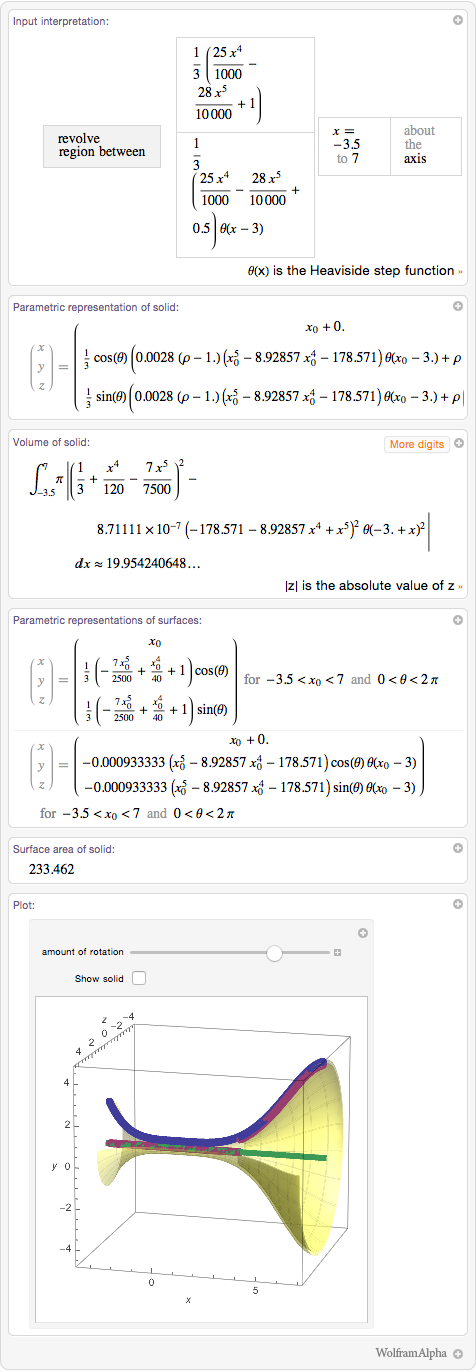
Хоть я и могу построить любую поверхность вращения в Wolfram Language с помощью RevolutionPlot3D, вместо этого я просто скопировал «Параметрическое представление поверхностей» и использовал его в ParametricPlot3D (а если вы хотите реализовать это через Wolfram|Alpha, то скопируйте «Текстовый ввод в Wolfram Language» из «Параметрического представления поверхностей» – часть вывода Wolfram|Alpha). Оказалось, что мне нужно было кое-что поменять, чтобы удовлетворить требованиям Shapeways: во-первых, необходимо было перевести сантиметры в миллиметры, чего я добился, увеличив все размеры в 10 раз (посредством ScalingTransform), а во-вторых мне нужно было задать толщину в 1.6 мм, что я реализовал с помощью PlotStyle:
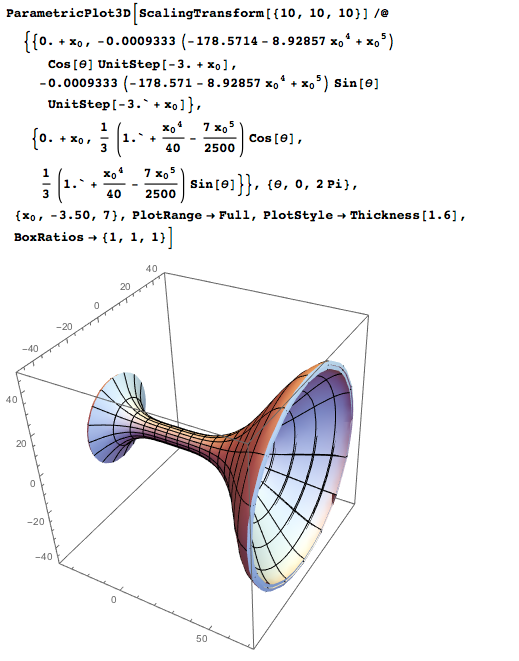
Единственное, что после этого потребовалось – загрузить чашку в .stl формате на их вебсайт:

И… вуаля! Вот изображение готового бокала, воплощенного в пластике (стоило это всё $23):

В Wolfram|Alpha можно создавать самые разнообразные поверхности и тела вращения, используя различные функции, оси и параметры вращения:
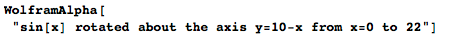
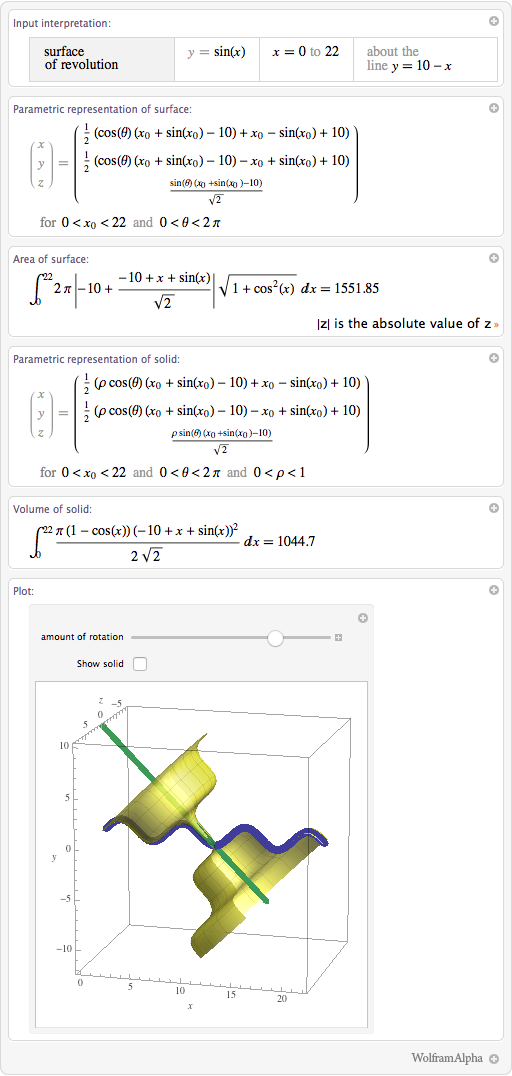
Я могу даже провращать бесконечно длинную часть кривой, что приведёт нас к математическому «парадоксу» под названием рога Гавриила (или труба Торричелли):
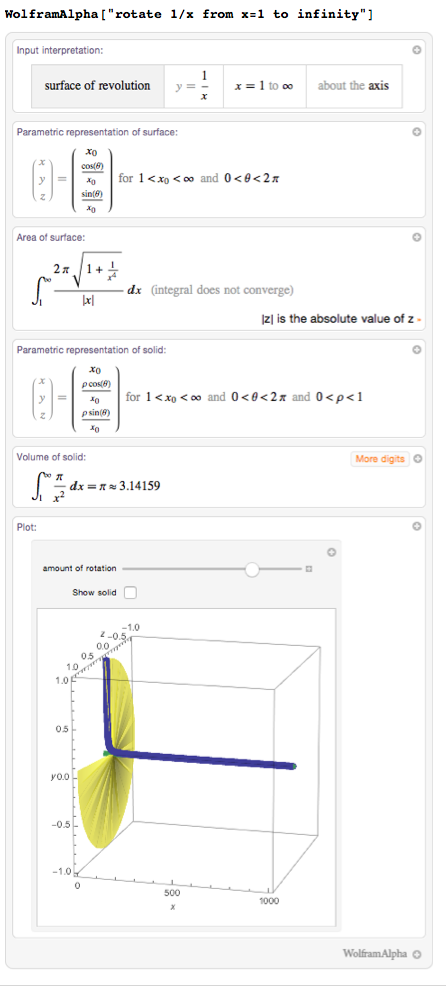
Wolfram|Alpha сообщает, что полученный объем равен π, однако площадь поверхности бесконечна! Кажется, из этого следует, что я могу заполнить рог конечным количеством краски, однако этого количества не должно хватить на то, чтобы покрыть всю внутреннюю поверхность – какой-то абсурд получается. Разумеется, слой краски на самом деле не является двумерным, и в некоторый момент трубка сузится настолько, что через неё больше не сможет пройти ни одной молекулы, так что с точки зрения физики мы не имеем никакого парадокса.
Вскоре пользователи Wolfram|Alpha Pro смогут получить доступ к пошаговым решениям задач о нахождении площади и объема поверхности вращения, показывающие, как можно вычислить отдельные составляющие поверхности или объема и объединить их вместе. Я был бы рад услышать от вас идеи о том, как еще можно использовать данную методику.
И вот, держа сейчас этот бокал в руках (отчасти потому, что я не учёл его склонность к опрокидыванию), я предлагаю тост: за творчество и за те инструменты, которые позволяют реализовать наши идеи. Будем!
ссылка на оригинал статьи http://habrahabr.ru/post/270279/


Добавить комментарий