
Важное уточнение — калькулятор обычный, без кнопки sin. Как в бухгалтерии или на рынке.
Простое решение
Первое, что приходит в голову — вот такое заклинание:
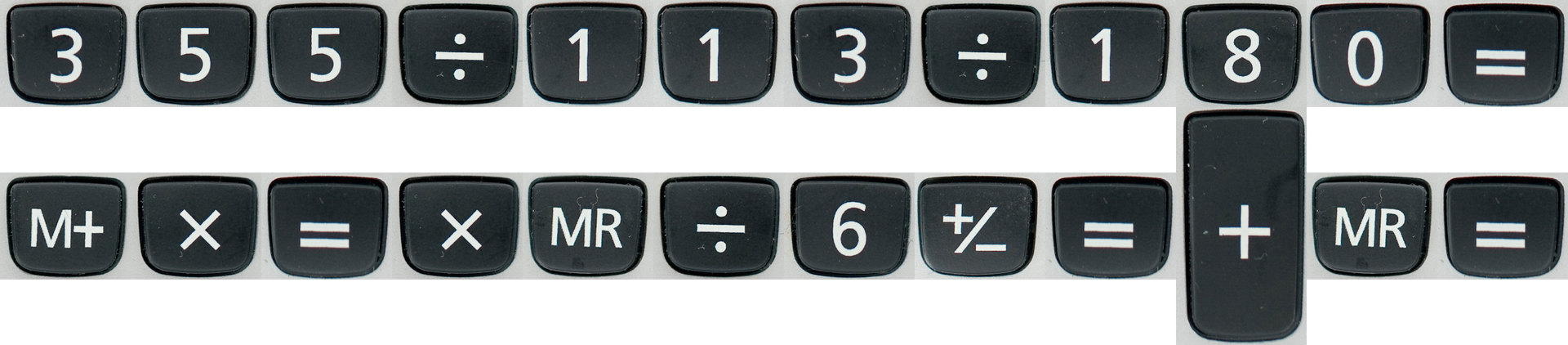
Переведём эту путаную партитуру для калькулятора на более понятный язык bc. Он часто используется как калькулятор в командной строке UNIX-подобных операционных систем. Увидим примерно следующее:
scale = 7 x = 355/113/180 x-x^3/6 .0174524
sin(x) ≅ x — x3/6
Перед подстановкой градус придётся перевести в радианы умножением на π и делением на 180°.
Отдельный приз полагается заметившим странные цифры 355 и 113. Их нашёл в наш китайский товарищ Цзу Чунчжи (祖沖之) ещё во времена династии Ци (479—502). Отношение 355/113 — это единственное приближение числа π рациональной дробью, которое короче десятичного представления аналогичной точности.
Интересное решение
Описанный выше общеизвестный трюк появился только в 1715 году. Тем не менее значения тригонометрических функций были известны намного раньше, и с заметно большей точностью.
Заведующий Самаркандской обсерваторией Гияс-ад-дин Джамшид ибн Масуд аль-Каши (غیاث الدین جمشید کاشانی) составил таблицы тригонометрических функций с точностью до 16-го знака ещё до 1429 года. В переводе с персидского на bc его заклинание применительно к нашей задаче выглядело примерно так:
scale = 16 sin30 = .5 cos30 = sqrt(3)/2 sin45 = sqrt(2)/2 cos45 = sin45 sin75 = sin30*cos45+cos30*sin45 cos75 = sqrt(1-sin75^2) cos36 = (1+sqrt(5))/4 sin36 = sqrt(1-cos36^2) sin72 = 2*sin36*cos36 cos72 = sqrt(1-sin72^2) (sin3 = sin75*cos72-cos75*sin72) .0523359562429430 (x = sin3/3) .0174453187476476 (x = (sin3+4*x^3)/3) .0174523978055315 (x = (sin3+4*x^3)/3) .0174524064267667 (x = (sin3+4*x^3)/3) .0174524064372703 (x = (sin3+4*x^3)/3) .0174524064372831 (x = (sin3+4*x^3)/3) .0174524064372831 Обратите внимание на то, что мы по-прежнему используем только сложение, вычитание, умножение, деление и квадратный корень. При желании все эти операции можно выполнить вообще на бумажке в столбик. Cчитать квадратный корень в столбик раньше даже учили в школе. Это занудно, но не очень сложно.
sin30 = .5 cos30 = sqrt(3)/2 sin45 = sqrt(2)/2 cos45 = sin45 Синус и косинус 30° и 45° были известны ещё древним грекам.
sin75 = sin30*cos45+cos30*sin45 Налицо синус суммы углов 30° и 45°. Ещё до аль-Каши эту формулу вывел другой персидский астроном, Абуль-Вафа Мухаммад ибн Мухаммад ибн Яхья ибн Исмаил ибн Аббас аль-Бузджани.
cos75 = sqrt(1-sin75^2) Пифагоровы штаны во все стороны равны.
cos36 = (1+sqrt(5))/4 sin36 = sqrt(1-cos36^2) Это из правильного пятиугольника, известного ещё древним грекам.
sin72 = 2*sin36*cos36 cos72 = sqrt(1-sin72^2) Опять синус суммы и теорема Пифагора.
(sin3 = sin75*cos72-cos75*sin72) .0523359562429430 Считаем синус разности 75° и 72° и получаем синус 3°.
Теперь можно разложить 3° на сумму трёх углов по 1°, но возникает заминка — получаем кубическое уравнение:
sin 3° = 3 x — 4 x3
где x = sin 1°. Решать кубические уравнения аналитически тогда ещё никто не умел.
Мудрый аль-Каши заметил, что можно выразить это уравнение в следующей форме:
f(x) = (sin 3° + 4 x3) / 3
и потом применить к f(x) метод простой итерации. Напоминаю, что в то время ни Ньютон, ни Рафсон ещё не родились.
(x = sin3/3) Первое приближение.
.0174453187476476 (x = (sin3+4*x^3)/3) .0174523978055315 (x = (sin3+4*x^3)/3) .0174524064267667 (x = (sin3+4*x^3)/3) .0174524064372703 (x = (sin3+4*x^3)/3) .0174524064372831 (x = (sin3+4*x^3)/3) .0174524064372831 Получаем 16 знаков после пяти итераций.
Как считает сам калькулятор
У пытливого читателя может возникнуть законный вопрос: как же считает значение синуса калькулятор, у которого есть такая кнопка?
Оказывается, что большинство калькуляторов используют совершенно третий способ — «цифра за цифрой», родившийся в недрах военно-промышленного комплекса США во время холодной войны.
Главное преимущество метода «цифра за цифрой» в том, что он использует только операции сложения и умножения на два (которое легко реализовать сдвигом влево).
Кроме того, алгоритм можно заставить работать прямо в двоично-десятичном коде, который используется в большинстве калькуляторов, но в приведённом ниже примере мы в эти дебри не полезем.
Алгоритм итеративный и использует таблицу арктангенсов, по одному на итерацию. Таблицу нужно посчитать заранее:
#include <stdio.h> #include <math.h> int main(int argc, char **argv) { int bits = 32; int cordic_one = 1 << (bits - 2); printf("// Число с фиксированной точкой, соответствующее единице с плавающей точкой\n"); printf("static const int cordic_one = 0x%08x;\n", cordic_one); printf("static const int cordic_table[] = {\n"); double k = 1; for (int i = 0; i < bits; i++) { printf("0x%08x, // 0x%08x * atan(1/%.0f) \n", (int)(atan(pow(2, -i)) * cordic_one), cordic_one, pow(2, i)); k /= sqrt(1 + pow(2, -2 * i)); } printf("};\n"); printf("static const int cordic_k = 0x%08x; // %.16f * 0x%08x\n", (int)(k * cordic_one), k, cordic_one); } Заодно считается масштабирующий коэффициент cordic_k.
После этого посчитать пресловутый sin 1° можно так:
#include <stdio.h> #include <math.h> // Число с фиксированной точкой, соответствующее единице с плавающей точкой static const int cordic_one = 0x40000000; static const int cordic_table[] = { 0x3243f6a8, // 0x40000000 * atan(1/1) 0x1dac6705, // 0x40000000 * atan(1/2) 0x0fadbafc, // 0x40000000 * atan(1/4) 0x07f56ea6, // 0x40000000 * atan(1/8) 0x03feab76, // 0x40000000 * atan(1/16) 0x01ffd55b, // 0x40000000 * atan(1/32) 0x00fffaaa, // 0x40000000 * atan(1/64) 0x007fff55, // 0x40000000 * atan(1/128) 0x003fffea, // 0x40000000 * atan(1/256) 0x001ffffd, // 0x40000000 * atan(1/512) 0x000fffff, // 0x40000000 * atan(1/1024) 0x0007ffff, // 0x40000000 * atan(1/2048) 0x0003ffff, // 0x40000000 * atan(1/4096) 0x0001ffff, // 0x40000000 * atan(1/8192) 0x0000ffff, // 0x40000000 * atan(1/16384) 0x00007fff, // 0x40000000 * atan(1/32768) 0x00003fff, // 0x40000000 * atan(1/65536) 0x00001fff, // 0x40000000 * atan(1/131072) 0x00000fff, // 0x40000000 * atan(1/262144) 0x000007ff, // 0x40000000 * atan(1/524288) 0x000003ff, // 0x40000000 * atan(1/1048576) 0x000001ff, // 0x40000000 * atan(1/2097152) 0x000000ff, // 0x40000000 * atan(1/4194304) 0x0000007f, // 0x40000000 * atan(1/8388608) 0x0000003f, // 0x40000000 * atan(1/16777216) 0x0000001f, // 0x40000000 * atan(1/33554432) 0x0000000f, // 0x40000000 * atan(1/67108864) 0x00000008, // 0x40000000 * atan(1/134217728) 0x00000004, // 0x40000000 * atan(1/268435456) 0x00000002, // 0x40000000 * atan(1/536870912) 0x00000001, // 0x40000000 * atan(1/1073741824) 0x00000000, // 0x40000000 * atan(1/2147483648) }; static const int cordic_k = 0x26dd3b6a; // 0.6072529350088813 * 0x40000000 void cordic(int theta, int& s, int& c) { c = cordic_k; s = 0; for (int k = 0; k < 32; ++k) { int d = (theta >= 0) ? 0 : -1; int tx = c - (((s >> k) ^ d) - d); int ty = s + (((c >> k) ^ d) - d); c = tx; s = ty; theta -= ((cordic_table[k] ^ d) - d); } } int main(void) { double alpha = M_PI / 180; int sine, cosine; cordic(alpha * cordic_one, sine, cosine); printf("CORDIC: %.8f\nExpected: %.8f\n", (double)sine / cordic_one, sin(alpha)); } Результат:
CORDIC: 0.01745240 Expected: 0.01745241 Тут 32 итерации, поэтому осталась небольшая ошибка. Калькуляторы обычно используют 40 итераций.
ссылка на оригинал статьи http://habrahabr.ru/post/271889/
Добавить комментарий