Нейросеть на Python, часть 2: градиентный спуск

Давай сразу код!

import numpy as np X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ]) y = np.array([[0,1,1,0]]).T alpha,hidden_dim = (0.5,4) synapse_0 = 2*np.random.random((3,hidden_dim)) - 1 synapse_1 = 2*np.random.random((hidden_dim,1)) - 1 for j in xrange(60000):     layer_1 = 1/(1+np.exp(-(np.dot(X,synapse_0))))     layer_2 = 1/(1+np.exp(-(np.dot(layer_1,synapse_1))))     layer_2_delta = (layer_2 - y)*(layer_2*(1-layer_2))     layer_1_delta = layer_2_delta.dot(synapse_1.T) * (layer_1 * (1-layer_1))     synapse_1 -= (alpha * layer_1.T.dot(layer_2_delta))     synapse_0 -= (alpha * X.T.dot(layer_1_delta))

Часть 1: Оптимизация

В первой части я описал основные принципы обратного распространения в простой нейросети. Сеть позволила нам померить, каким образом каждый из весов сети вносит свой вклад в ошибку. И это позволило нам менять веса при помощи другого алгоритма — градиентного спуска.

Суть происходящего в том, что обратное распространение не вносит в работу сети оптимизацию. Оно перемещает неверную информацию с конца сети на все веса внутри, чтобы другой алгоритм уже смог оптимизировать эти веса так, чтобы они соответствовали нашим данным. Но в принципе, у нас в изобилии присутствуют и другие методы нелинейной оптимизации, которые мы можем использовать с обратным распространением:

Некоторые методы оптимизации:

Визуализация разницы:

Разные методы подходят для разных случаев, и в некоторых случаях могут даже быть скомбинированы. В этом уроке мы рассмотрим градиентный спуск – это один из простейших и популярных алгоритмов оптимизации нейросетей. Таким образом мы улучшим нашу нейросеть через настройки и параметризацию.

Часть 2: Градиентный спуск

Допустим, у вас в круглой корзине есть красный мяч (картинка снизу). Мяч пытается найти дно. Это оптимизация. В нашем случае мяч оптимизирует свою позицию, слева направо, в поисках нижайшей точки в ведре.

У мяча есть два варианта движения – влево или вправо. Цель – занять позицию как можно ниже. Если вы управляли бы мячом с клавиатуры, вам нужно было бы нажимать кнопки влево и вправо.

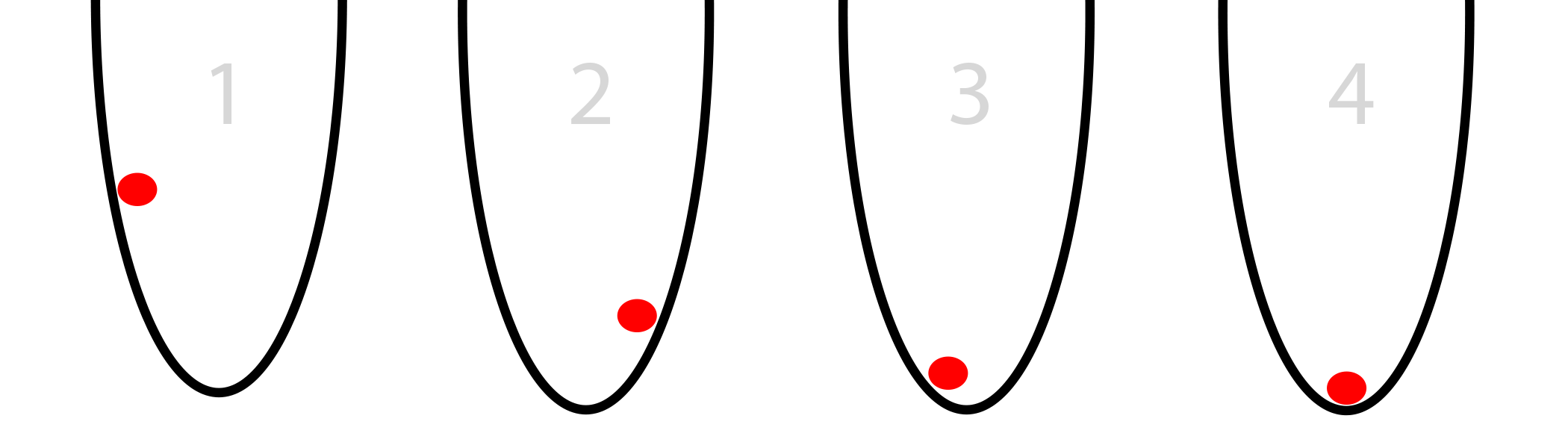
В нашем случае, мячу известен только уклон стороны ведра на его текущей позиции (касательная к стене, изображённая синим цветом). Заметьте, что если уклон отрицательный, мячу нужно двигаться вправо. Если положительный – влево. Очевидно, что этой информации вполне достаточно, чтобы найти дно ведра за несколько итераций. Такого рода оптимизация называется градиентной оптимизацией.

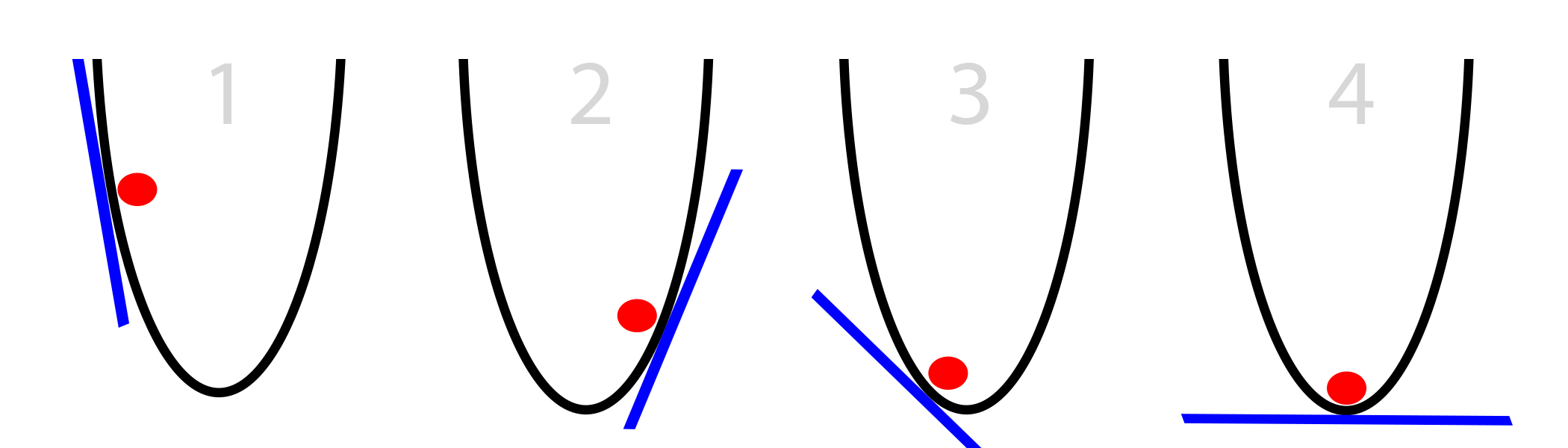
Простейший случай ГС:

вычислим уклон в нашей точке
если он отрицательный, двигаемся вправо
если он положительный, двигаемся влево
повторим, пока уклон не будет равен 0

Вопрос в том, на какое расстояние мяч должен двигаться на каждом шаге. Из картинки видно, что чем дальше он от дна, тем круче уклон. Усовершенствуем алгоритм, пользуясь этим знанием. Также примем, что ведро расположено на плоскости (х, у). Значит, положение мяча определяется координатой х. Увеличение х приводит к перемещению мяча вправо.

Простейший градиентный спуск:

подсчитать уклон slope на текущей позиции х
уменьшить х на slope (x = x — slope)
повторять, пока slope не станет равен 0

Этот алгоритм уже немного оптимизирован, ибо в случае большого уклона мы совершаем значительные сдвиги, а для небольших уклонов делаем небольшой сдвиг. В результате при приближении к дну корзины мяч совершает всё уменьшающиеся колебания, пока не достигнет точки с нулевым уклоном. Это будет точка сходимости.

Часть 3: Иногда это не срабатывает

Градиентный спуск несовершенен. Рассмотрим его проблемы и то, как люди их обходят.

Проблема 1: слишком большой уклон

Наш шаг зависит от величины уклона. Если он слишком большой, мы можем перепрыгнуть нужную нам точку. Если мы перепрыгнем её не очень сильно, это не страшно. Но можно перепрыгнуть её так сильно, что мы окажемся даже дальше от неё, чем были до этого.

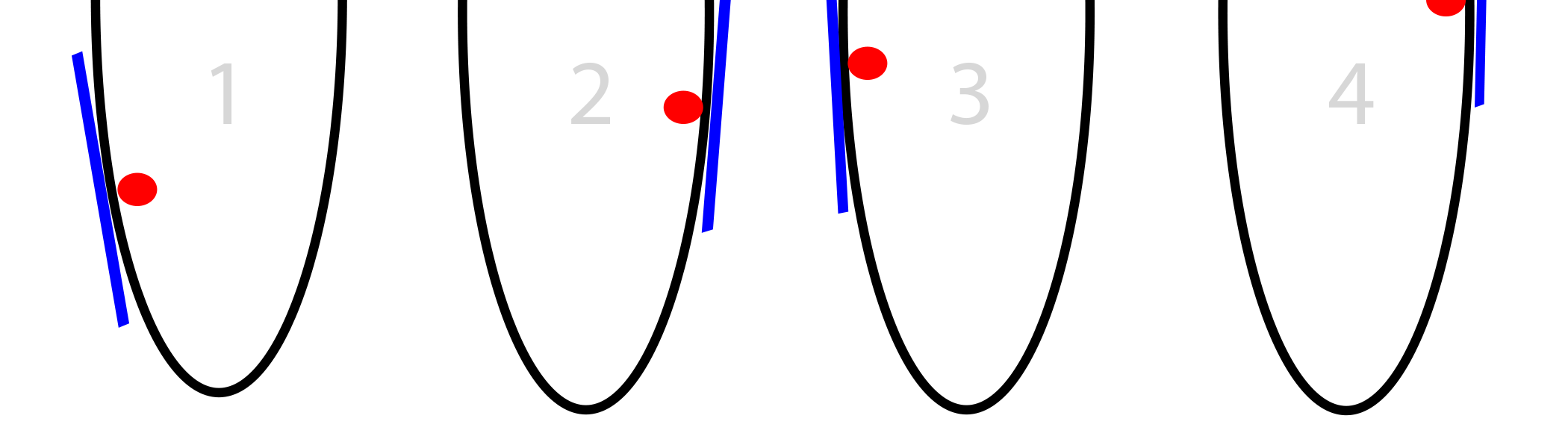
А уже там мы, естественно, найдём ещё больший уклон, прыгнем ещё дальше, и получим расходимость.

Решение 1: уменьшим уклоны

Просто помножим их на число от 0 до 1 (например, 0,01). Назовём эту константу alpha. После такого приведения наша сеть будет сходиться, ибо мы уже не перепрыгнем нужную точку так сильно.

Улучшенный градиентный спуск:

alpha = 0.1 (или любое число от 0 до 1)

Подсчитать уклон «slope» в текущем положении «x»
x = x — (alpha*slope)
(Повторять до тех пор, пока slope == 0)

Проблема 2: локальные минимумы

Иногда у ведра очень хитрая форма, и простое следование за уклоном не приведёт вас к абсолютному минимуму.

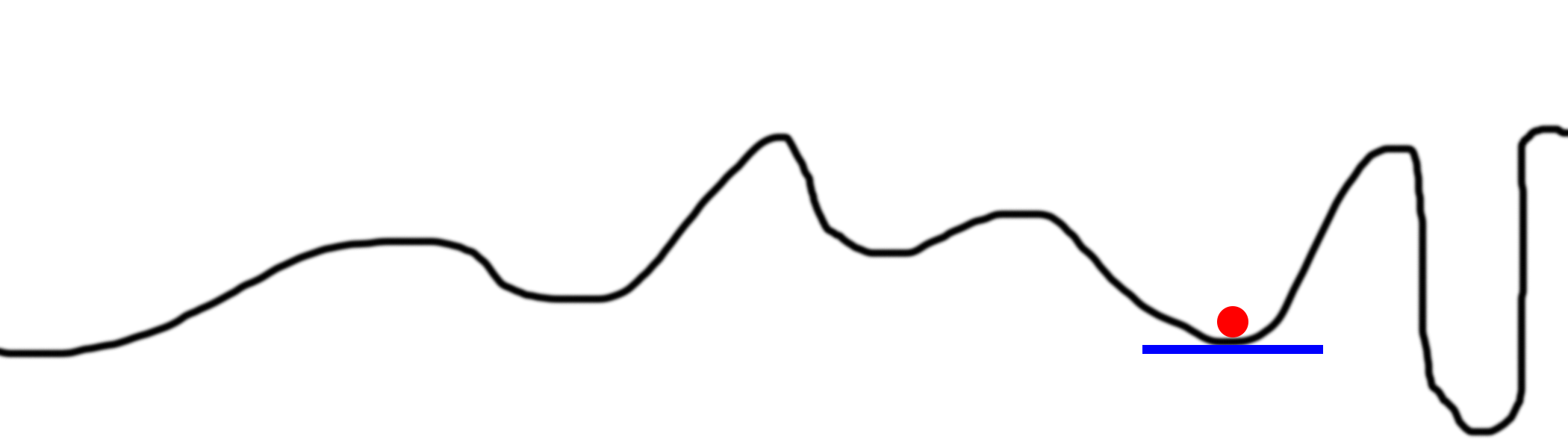
Это самая сложная проблема градиентного спуска. Существует множество методов её обхода. Обычно в них используется случайный поиск, пробующий разные части ведра.

Решение 2: множественные случайные стартовые точки

Хорошо, но если мы используем случайность для поиска глобального минимума, зачем нам вообще заниматься оптимизацией? Может, и решение будем искать случайным образом?

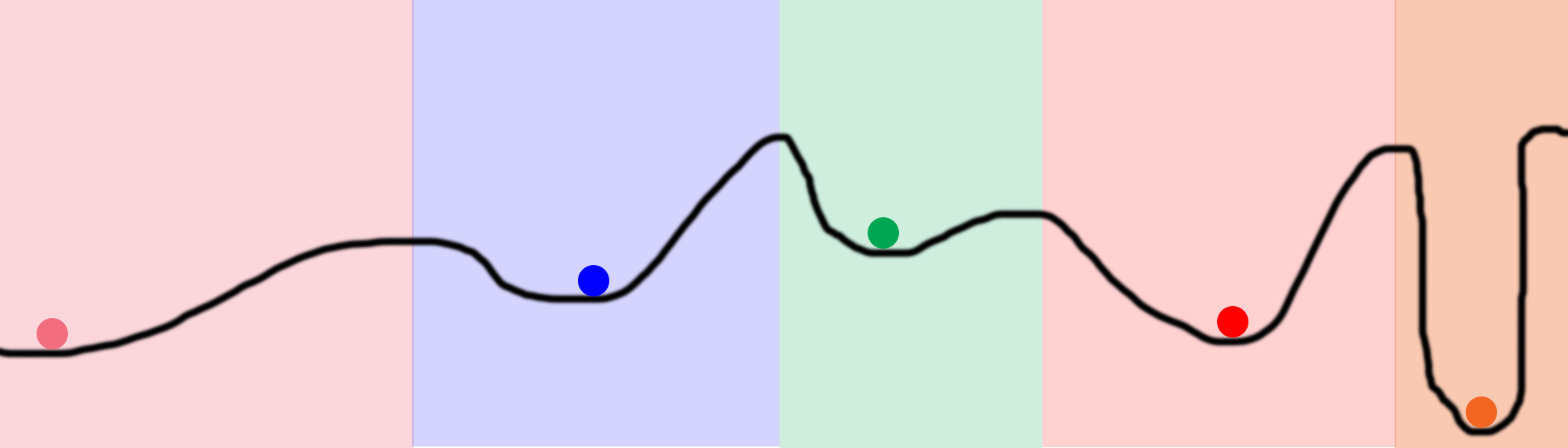
Рассмотрим этот график. Допустим, мы разместили на линии 100 мячей и начали их оптимизировать. В результате они окажутся на 5 позициях, отмеченных цветными кружками. Цветные области обозначают владения каждого локального минимума. К примеру, если мяч попадает в голубую область, он в результате окажется в синем минимуме. То есть, чтобы обследовать всё пространство, нам нужно случайно найти всего лишь 5 мест. Это гораздо лучше, чем полностью случайный поиск, который пробует каждое место на линии.

Касательно нейросетей, этого можно достичь, задав очень большие скрытые уровни. Каждый скрытый узел в уровне начинает работу в своём случайном состоянии. Тогда каждый узел сходится к какому-то своему конечному состоянию. Их размер может позволить пользователю сети попробовать тысячи, или миллионы, различных локальных минимумов в одной сети.

Примечание 1: этим нейросети и выгодны. У них есть возможность обыскивать пространство, не просчитывая его целиком. Мы можем обыскать всю чёрную линию на рисунке вверху, используя всего 5 мячей и небольшое количество итераций. Поиск методом грубой силы потребовал бы на несколько порядков больше процессорных мощностей.

Примечание 2: пытливый читатель спросит: «Зачем же нам позволять куче разных узлов сходиться к одной и той же точке? Это же трата вычислительных мощностей!». Хороший вопрос. Есть и такие подходы, избегающие скрытых узлов – это Dropout и Drop-Connect, которые я собираюсь описать позднее.

Проблема 3: уклоны слишком малы

Иногда уклоны бывают слишком малы. Рассмотрим такой график.

Наш мяч застрял. Это случится, если alpha будет слишком малой. Он сразу находит локальный минимум и игнорирует всё остальное. И, конечно же, с такими мелкими перемещениями сходимость займёт очень много времени.

Решение 3: увеличить alpha

Очевидно, можно увеличить alpha, и даже умножить наши дельты на число больше, чем 1. Это редко используется, но бывает.

Часть 4: стохастический градиентный спуск в нейросетях

Так как же эти мячи и линии связаны с нейросетями и обратным распространением? Эта тема настолько же важна, насколько и сложна.

В нейросети мы стараемся минимизировать ошибки по отношению к весам. Линия представляет ошибку сети относительно позиции одного из весов. Если бы мы подсчитали ошибку сети для любого возможного значения одного из весов, результат был бы представлен такой линией. Затем мы бы выбрали значение веса, соответствующего наименьшей ошибке (самая нижняя часть кривой). Я говорю – одного веса, поскольку наш график двумерный. х – это значение веса, а у – это ошибка нейросети в тот момент, когда вес находится в значении х.

Теперь рассмотрим, как этот процесс работает в простой двухуровневой нейросети.

import numpy as np  # подсчитаем нелинейную сигмоиду def sigmoid(x):     output = 1/(1+np.exp(-x))     return output  # преобразуем результат сигмоиды к производной def sigmoid_output_to_derivative(output):     return output*(1-output)      # входные данные X = np.array([  [0,1],                 [0,1],                 [1,0],                 [1,0] ])      # выходные данные       y = np.array([[0,0,1,1]]).T  # сделаем случайные числа детерминированными np.random.seed(1)  # случайная инициализация весов со средним 0 synapse_0 = 2*np.random.random((2,1)) - 1  for iter in xrange(10000):      # прямое распространение     layer_0 = X     layer_1 = sigmoid(np.dot(layer_0,synapse_0))      # как сильно ошиблись?     layer_1_error = layer_1 - y      # умножим ошибку на уклон сигмоиды      # со значениями в l1     layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)     synapse_0_derivative = np.dot(layer_0.T,layer_1_delta)      # обновим веса     synapse_0 -= synapse_0_derivative  print "Вывод после тренировки:" print layer_1

В нашем случае будет одна ошибка на выводе, подсчитываемая в строке 35 (layer_1_error = layer_1 — y). Так как у нас 2 веса, то график с ошибками будет расположен в трёхмерном пространстве. Это будет пространство (x,y,z), где по вертикали идут ошибки, а х и у – это значения весов в syn0.

Попробуем нарисовать поверхность ошибок для нашего набора данных. Как мы подсчитываем ошибку для данного набора весов? Этот подсчёт идёт в строках 31, 32 и 35:

layer_0 = X layer_1 = sigmoid(np.dot(layer_0,synapse_0)) layer_1_error = layer_1 - y

Если мы нарисуем общую ошибку для любого набора весов (от -10 до 10 для х и у), мы получим нечто вроде этого:

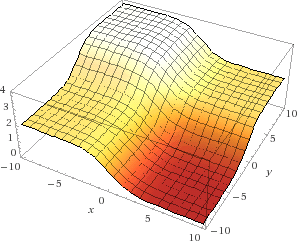
На самом деле всё просто – подсчитываем все возможные комбинации весов, и ошибку, выдаваемую сетью на каждом из наборов. х – первый вес synapse_0, а y – второй вес synapse_0. z – ошибка. Как видим, выходные данные положительно коррелируют с первым входным набором. Поэтому ошибка минимальна, когда х большой. А что насчёт у? Когда он оптимален?

Как оптимизируется наша двухуровневая сеть?

Значит, если указанные 3 строки подсчитывают ошибку, то следующие оптимизируют сеть для её уменьшения. Тут и происходит градиентный спуск.

layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1) synapse_0_derivative = np.dot(layer_0.T,layer_1_delta) synapse_0 -= synapse_0_derivative

Вспомним наш псевдокод:

подсчитать уклон slope на текущей позиции х
уменьшить х на slope (x = x — slope)
повторять, пока slope не станет равен 0

Это он и есть. Изменение состоит только в том, что мы оптимизируем 2 веса, а не один. Логика всё та же.

Часть 5: Улучшаем нейросеть

Улучшение 1: добавляем и настраиваем альфу

Что есть альфа? Как описано выше, этот параметр уменьшает размер каждого итерационного обновления. В последний момент, перед обновлением весов, мы умножаем размер обновления на alpha (обычно между 0 и 1). И такое минимальное изменение кода сильнейшим образом влияет на его способность тренироваться.

Вернёмся к нашей трёхуровневой сети из предыдущей статьи и добавим параметр альфа в нужное место. Затем мы проведём эксперименты, чтобы привести в соответствие все наши представления об alpha с реальным кодом.

Подсчитать уклон «slope» в текущем положении «x»
Уменьшить х на величину уклона, масштабированную при помощи alpha x = x — (alpha*slope)
(Повторять до тех пор, пока slope == 0)

import numpy as np  alphas = [0.001,0.01,0.1,1,10,100,1000]  # подсчитаем нелинейную сигмоиду def sigmoid(x):     output = 1/(1+np.exp(-x))     return output  # преобразуем результат сигмоиды к производной def sigmoid_output_to_derivative(output):     return output*(1-output)      X = np.array([[0,0,1],             [0,1,1],             [1,0,1],             [1,1,1]])                  y = np.array([[0], 			[1], 			[1], 			[0]])  for alpha in alphas:     print "\nТренируемся при Alpha:" + str(alpha)     np.random.seed(1)      # случайная инициализация весов со средним 0     synapse_0 = 2*np.random.random((3,4)) - 1     synapse_1 = 2*np.random.random((4,1)) - 1      for j in xrange(60000):          # Прямое распространение по уровням 0, 1 и 2         layer_0 = X         layer_1 = sigmoid(np.dot(layer_0,synapse_0))         layer_2 = sigmoid(np.dot(layer_1,synapse_1))          # как сильно ошиблись?         layer_2_error = layer_2 - y          if (j% 10000) == 0:             print "Ошибка после "+str(j)+" повторений:" + str(np.mean(np.abs(layer_2_error)))          # в каком направлении цель?         # уверены ли мы? Если да, то не нужно слишком сильных изменений         layer_2_delta = layer_2_error*sigmoid_output_to_derivative(layer_2)          # насколько каждое значение из l1 влияет на ошибку в l2 (в соответствии с весами)?         layer_1_error = layer_2_delta.dot(synapse_1.T)          # в каком направлении цель l1?         # уверены ли мы? Если да, то не нужно слишком сильных изменений         layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)          synapse_1 -= alpha * (layer_1.T.dot(layer_2_delta))         synapse_0 -= alpha * (layer_0.T.dot(layer_1_delta))

Тренировка с alpha:0.001 Ошибка после 0 повторений:0.496410031903 Ошибка после 10000 повторений:0.495164025493 Ошибка после 20000 повторений:0.493596043188 Ошибка после 30000 повторений:0.491606358559 Ошибка после 40000 повторений:0.489100166544 Ошибка после 50000 повторений:0.485977857846  Тренировка с alpha:0.01 Ошибка после 0 повторений:0.496410031903 Ошибка после 10000 повторений:0.457431074442 Ошибка после 20000 повторений:0.359097202563 Ошибка после 30000 повторений:0.239358137159 Ошибка после 40000 повторений:0.143070659013 Ошибка после 50000 повторений:0.0985964298089  Тренировка с alpha:0.1 Ошибка после 0 повторений:0.496410031903 Ошибка после 10000 повторений:0.0428880170001 Ошибка после 20000 повторений:0.0240989942285 Ошибка после 30000 повторений:0.0181106521468 Ошибка после 40000 повторений:0.0149876162722 Ошибка после 50000 повторений:0.0130144905381  Тренировка с alpha:1 Ошибка после 0 повторений:0.496410031903 Ошибка после 10000 повторений:0.00858452565325 Ошибка после 20000 повторений:0.00578945986251 Ошибка после 30000 повторений:0.00462917677677 Ошибка после 40000 повторений:0.00395876528027 Ошибка после 50000 повторений:0.00351012256786  Тренировка с alpha:10 Ошибка после 0 повторений:0.496410031903 Ошибка после 10000 повторений:0.00312938876301 Ошибка после 20000 повторений:0.00214459557985 Ошибка после 30000 повторений:0.00172397549956 Ошибка после 40000 повторений:0.00147821451229 Ошибка после 50000 повторений:0.00131274062834  Тренировка с alpha:100 Ошибка после 0 повторений:0.496410031903 Ошибка после 10000 повторений:0.125476983855 Ошибка после 20000 повторений:0.125330333528 Ошибка после 30000 повторений:0.125267728765 Ошибка после 40000 повторений:0.12523107366 Ошибка после 50000 повторений:0.125206352756  Тренировка с alpha:1000 Ошибка после 0 повторений:0.496410031903 Ошибка после 10000 повторений:0.5 Ошибка после 20000 повторений:0.5 Ошибка после 30000 повторений:0.5 Ошибка после 40000 повторений:0.5 Ошибка после 50000 повторений:0.5

Какие можно сделать выводы из разных величин alpha?

Alpha = 0.001
При очень низком значении сеть вообще не сходится. Обновления весов слишком малы. Мало что поменялось даже после 60000 итераций. Это наша проблема №3: когда уклоны слишком малы.

Alpha = 0.01
Неплохое схождение, плавно проходившее за 60000 повторений, но всё равно не сошлось так близко к цели, как другие случаи. Та же проблема №3.

Alpha = 0.1
Вначале шли довольно быстро, но затем замедлились. Это всё ещё 3-я проблема.

Alpha = 1
Пытливый читатель заметит, что сходимость в данном случае точно такая же, как если бы никакой альфы не было. Мы умножаем на 1.

Alpha = 10
Сюрприз – альфа больше единицы привела к достижению результата всего за 10000 повторений. Значит, наше обновление весов до этого было слишком малым. Значит, веса двигались в нужном направлении, просто до этого они двигались слишком медленно.

Alpha = 100
Слишком большие величины оказываются контрпродуктивными. Шаги сети такие большие, что она не может найти нижнюю точку на поверхности ошибок. Это наша проблема №1. Сеть просто прыгает туда-сюда по поверхности ошибок и нигде не находит минимум.

Alpha = 1000
Происходит увеличение ошибки вместо уменьшения, и оно останавливается на значении 0,5. Это более экстремальный вариант проблемы №3.

Рассмотрим результаты поближе

import numpy as np  alphas = [0.001,0.01,0.1,1,10,100,1000]  # подсчитаем нелинейную сигмоиду def sigmoid(x):     output = 1/(1+np.exp(-x))     return output  # преобразуем результат сигмоиды к производной def sigmoid_output_to_derivative(output):     return output*(1-output)      X = np.array([[0,0,1],             [0,1,1],             [1,0,1],             [1,1,1]])                  y = np.array([[0], 			[1], 			[1], 			[0]])  for alpha in alphas:     print "\nТренировка с alpha:" + str(alpha)     np.random.seed(1)      # случайная инициализация весов со средним 0     synapse_0 = 2*np.random.random((3,4)) - 1     synapse_1 = 2*np.random.random((4,1)) - 1              prev_synapse_0_weight_update = np.zeros_like(synapse_0)     prev_synapse_1_weight_update = np.zeros_like(synapse_1)      synapse_0_direction_count = np.zeros_like(synapse_0)     synapse_1_direction_count = np.zeros_like(synapse_1)              for j in xrange(60000):          # Прямое распространение по уровням 0, 1 и 2         layer_0 = X         layer_1 = sigmoid(np.dot(layer_0,synapse_0))         layer_2 = sigmoid(np.dot(layer_1,synapse_1))          # как сильно ошиблись?         layer_2_error = y - layer_2          if (j% 10000) == 0:             print "Error:" + str(np.mean(np.abs(layer_2_error)))          # в каком направлении цель?         # уверены ли мы? Если да, то не нужно слишком сильных изменений         layer_2_delta = layer_2_error*sigmoid_output_to_derivative(layer_2)          # насколько каждое значение из l1 влияет на ошибку в l2 (в соответствии с весами)?         layer_1_error = layer_2_delta.dot(synapse_1.T)          # в каком направлении цель l1?         # уверены ли мы? Если да, то не нужно слишком сильных изменений         layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)                  synapse_1_weight_update = (layer_1.T.dot(layer_2_delta))         synapse_0_weight_update = (layer_0.T.dot(layer_1_delta))                  if(j > 0):             synapse_0_direction_count += np.abs(((synapse_0_weight_update > 0)+0) - ((prev_synapse_0_weight_update > 0) + 0))             synapse_1_direction_count += np.abs(((synapse_1_weight_update > 0)+0) - ((prev_synapse_1_weight_update > 0) + 0))                          synapse_1 += alpha * synapse_1_weight_update         synapse_0 += alpha * synapse_0_weight_update                  prev_synapse_0_weight_update = synapse_0_weight_update         prev_synapse_1_weight_update = synapse_1_weight_update          print "Synapse 0"     print synapse_0          print "Synapse 0 Update Direction Changes"     print synapse_0_direction_count          print "Synapse 1"     print synapse_1      print "Synapse 1 Update Direction Changes"     print synapse_1_direction_count

Тренировка с alpha:0.001 Error:0.496410031903 Error:0.495164025493 Error:0.493596043188 Error:0.491606358559 Error:0.489100166544 Error:0.485977857846 Synapse 0 [[-0.28448441  0.32471214 -1.53496167 -0.47594822]  [-0.7550616  -1.04593014 -1.45446052 -0.32606771]  [-0.2594825  -0.13487028 -0.29722666  0.40028038]] Synapse 0 Update Direction Changes [[ 0.  0.  0.  0.]  [ 0.  0.  0.  0.]  [ 1.  0.  1.  1.]] Synapse 1 [[-0.61957526]  [ 0.76414675]  [-1.49797046]  [ 0.40734574]] Synapse 1 Update Direction Changes [[ 1.]  [ 1.]  [ 0.]  [ 1.]]  Тренировка с alpha:0.01 Error:0.496410031903 Error:0.457431074442 Error:0.359097202563 Error:0.239358137159 Error:0.143070659013 Error:0.0985964298089 Synapse 0 [[ 2.39225985  2.56885428 -5.38289334 -3.29231397]  [-0.35379718 -4.6509363  -5.67005693 -1.74287864]  [-0.15431323 -1.17147894  1.97979367  3.44633281]] Synapse 0 Update Direction Changes [[ 1.  1.  0.  0.]  [ 2.  0.  0.  2.]  [ 4.  2.  1.  1.]] Synapse 1 [[-3.70045078]  [ 4.57578637]  [-7.63362462]  [ 4.73787613]] Synapse 1 Update Direction Changes [[ 2.]  [ 1.]  [ 0.]  [ 1.]]  Тренировка с alpha:0.1 Error:0.496410031903 Error:0.0428880170001 Error:0.0240989942285 Error:0.0181106521468 Error:0.0149876162722 Error:0.0130144905381 Synapse 0 [[ 3.88035459  3.6391263  -5.99509098 -3.8224267 ]  [-1.72462557 -5.41496387 -6.30737281 -3.03987763]  [ 0.45953952 -1.77301389  2.37235987  5.04309824]] Synapse 0 Update Direction Changes [[ 1.  1.  0.  0.]  [ 2.  0.  0.  2.]  [ 4.  2.  1.  1.]] Synapse 1 [[-5.72386389]  [ 6.15041318]  [-9.40272079]  [ 6.61461026]] Synapse 1 Update Direction Changes [[ 2.]  [ 1.]  [ 0.]  [ 1.]]  Тренировка с alpha:1 Error:0.496410031903 Error:0.00858452565325 Error:0.00578945986251 Error:0.00462917677677 Error:0.00395876528027 Error:0.00351012256786 Synapse 0 [[ 4.6013571   4.17197193 -6.30956245 -4.19745118]  [-2.58413484 -5.81447929 -6.60793435 -3.68396123]  [ 0.97538679 -2.02685775  2.52949751  5.84371739]] Synapse 0 Update Direction Changes [[ 1.  1.  0.  0.]  [ 2.  0.  0.  2.]  [ 4.  2.  1.  1.]] Synapse 1 [[ -6.96765763]  [  7.14101949]  [-10.31917382]  [  7.86128405]] Synapse 1 Update Direction Changes [[ 2.]  [ 1.]  [ 0.]  [ 1.]]  Тренировка с alpha:10 Error:0.496410031903 Error:0.00312938876301 Error:0.00214459557985 Error:0.00172397549956 Error:0.00147821451229 Error:0.00131274062834 Synapse 0 [[ 4.52597806  5.77663165 -7.34266481 -5.29379829]  [ 1.66715206 -7.16447274 -7.99779235 -1.81881849]  [-4.27032921 -3.35838279  3.44594007  4.88852208]] Synapse 0 Update Direction Changes [[  7.  19.   2.   6.]  [  7.   2.   0.  22.]  [ 19.  26.   9.  17.]] Synapse 1 [[ -8.58485788]  [ 10.1786297 ]  [-14.87601886]  [  7.57026121]] Synapse 1 Update Direction Changes [[ 22.]  [ 15.]  [  4.]  [ 15.]]  Тренировка с alpha:100 Error:0.496410031903 Error:0.125476983855 Error:0.125330333528 Error:0.125267728765 Error:0.12523107366 Error:0.125206352756 Synapse 0 [[-17.20515374   1.89881432 -16.95533155  -8.23482697]  [  5.70240659 -17.23785161  -9.48052574  -7.92972576]  [ -4.18781704  -0.3388181    2.82024759  -8.40059859]] Synapse 0 Update Direction Changes [[  8.   7.   3.   2.]  [ 13.   8.   2.   4.]  [ 16.  13.  12.   8.]] Synapse 1 [[  9.68285369]  [  9.55731916]  [-16.0390702 ]  [  6.27326973]] Synapse 1 Update Direction Changes [[ 13.]  [ 11.]  [ 12.]  [ 10.]]  Тренировка с alpha:1000 Error:0.496410031903 Error:0.5 Error:0.5 Error:0.5 Error:0.5 Error:0.5 Synapse 0 [[-56.06177241  -4.66409623  -5.65196179 -23.05868769]  [ -4.52271708  -4.78184499 -10.88770202 -15.85879101]  [-89.56678495  10.81119741  37.02351518 -48.33299795]] Synapse 0 Update Direction Changes [[ 3.  2.  4.  1.]  [ 1.  2.  2.  1.]  [ 6.  6.  4.  1.]] Synapse 1 [[  25.16188889]  [  -8.68235535]  [-116.60053379]  [  11.41582458]] Synapse 1 Update Direction Changes [[ 7.]  [ 7.]  [ 7.]  [ 3.]]

В приведённом коде я подсчитываю количество раз, когда производная меняет направление. Этому соответствует вывод «Update Direction Changes». Если уклон (производная) меняет направление, значит, мы прошли над локальным минимумом и нам надо вернуться. Если она не меняет направление, значит мы, вероятно, не очень далеко продвинулись.

Что видим:

Когда альфа была мелкой, производная почти никогда не меняла направления
Когда альфа оптимальна, производная часто меняет направление
Когда альфа большая, производная не очень часто меняет направление
Когда альфа мелкая, веса получаются мелкими
Когда альфа большая, веса также увеличиваются

Улучшение 2: параметризация размера скрытого уровня

Увеличение размера скрытого уровня увеличивает размер пространства для поисков, к которому мы сходимся на каждом повторении. Рассмотрим такую сеть и её вывод.

import numpy as np  alphas = [0.001,0.01,0.1,1,10,100,1000] hiddenSize = 32  # подсчитаем нелинейную сигмоиду def sigmoid(x):     output = 1/(1+np.exp(-x))     return output  # преобразуем результат сигмоиды к производной def sigmoid_output_to_derivative(output):     return output*(1-output)      X = np.array([[0,0,1],             [0,1,1],             [1,0,1],             [1,1,1]])                  y = np.array([[0], 			[1], 			[1], 			[0]])  for alpha in alphas:     print "\nТренировка с alpha:" + str(alpha)     np.random.seed(1)      # randomly initialize our weights with mean 0     synapse_0 = 2*np.random.random((3,hiddenSize)) - 1     synapse_1 = 2*np.random.random((hiddenSize,1)) - 1      for j in xrange(60000):          # Прямое распространение по уровням 0, 1 и 2         layer_0 = X         layer_1 = sigmoid(np.dot(layer_0,synapse_0))         layer_2 = sigmoid(np.dot(layer_1,synapse_1))          # как сильно ошиблись?         layer_2_error = layer_2 - y          if (j% 10000) == 0:             print "Ошибка после "+str(j)+" повторений:" + str(np.mean(np.abs(layer_2_error)))          # в каком направлении цель?         # уверены ли мы? Если да, то не нужно слишком сильных изменений         layer_2_delta = layer_2_error*sigmoid_output_to_derivative(layer_2)          # насколько каждое значение из l1 влияет на ошибку в l2 (в соответствии с весами)?         layer_1_error = layer_2_delta.dot(synapse_1.T)          # в каком направлении цель l1?         # уверены ли мы? Если да, то не нужно слишком сильных изменений         layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)          synapse_1 -= alpha * (layer_1.T.dot(layer_2_delta))         synapse_0 -= alpha * (layer_0.T.dot(layer_1_delta))

Тренировка с alpha:0.001 Ошибка после 0 повторений:0.496439922501 Ошибка после 10000 повторений:0.491049468129 Ошибка после 20000 повторений:0.484976307027 Ошибка после 30000 повторений:0.477830678793 Ошибка после 40000 повторений:0.46903846539 Ошибка после 50000 повторений:0.458029258565  Тренировка с alpha:0.01 Ошибка после 0 повторений:0.496439922501 Ошибка после 10000 повторений:0.356379061648 Ошибка после 20000 повторений:0.146939845465 Ошибка после 30000 повторений:0.0880156127416 Ошибка после 40000 повторений:0.065147819275 Ошибка после 50000 повторений:0.0529658087026  Тренировка с alpha:0.1 Ошибка после 0 повторений:0.496439922501 Ошибка после 10000 повторений:0.0305404908386 Ошибка после 20000 повторений:0.0190638725334 Ошибка после 30000 повторений:0.0147643907296 Ошибка после 40000 повторений:0.0123892429905 Ошибка после 50000 повторений:0.0108421669738  Тренировка с alpha:1 Ошибка после 0 повторений:0.496439922501 Ошибка после 10000 повторений:0.00736052234249 Ошибка после 20000 повторений:0.00497251705039 Ошибка после 30000 повторений:0.00396863978159 Ошибка после 40000 повторений:0.00338641021983 Ошибка после 50000 повторений:0.00299625684932  Тренировка с alpha:10 Ошибка после 0 повторений:0.496439922501 Ошибка после 10000 повторений:0.00224922117381 Ошибка после 20000 повторений:0.00153852153014 Ошибка после 30000 повторений:0.00123717718456 Ошибка после 40000 повторений:0.00106119569132 Ошибка после 50000 повторений:0.000942641990774  Тренировка с alpha:100 Ошибка после 0 повторений:0.496439922501 Ошибка после 10000 повторений:0.5 Ошибка после 20000 повторений:0.5 Ошибка после 30000 повторений:0.5 Ошибка после 40000 повторений:0.5 Ошибка после 50000 повторений:0.5  Тренировка с alpha:1000 Ошибка после 0 повторений:0.496439922501 Ошибка после 10000 повторений:0.5 Ошибка после 20000 повторений:0.5 Ошибка после 30000 повторений:0.5 Ошибка после 40000 повторений:0.5 Ошибка после 50000 повторений:0.5

Наилучшая ошибка с 32 узлами — 0.0009, тогда как наилучшая ошибка с 4 скрытыми узлами – только 0.0013. Это достаточно важно. Для представления нашего набора данных нам не нужно более 3 узлов. Но поскольку у нас было больше узлов, мы провели поиск в большем пространстве при каждом повторении, и схождение получилось быстрее. В нашем случае разница невелика, но при работе со сложными наборами данных это очень важно.

ссылка на оригинал статьи http://habrahabr.ru/post/272679/