Расчет биномиальных коэффициентов на Си (С++)

При решении задач комбинаторики часто возникает необходимость в расчете биномиальные коэффициентов. Бином Ньютона, т.е. разложение 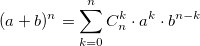также использует биномиальные коэффициенты. Для их расчета можно использовать формулу, выражающую биномиальный коэффициент через факториалы: 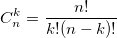или использовать рекуррентную формулу: 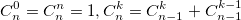Из бинома Ньютона и рекуррентной формулы ясно, что биномиальные коэффициенты — целые числа.
Прежде чем перейти к написанию процедур расчета, рассмотрим так называемый треугольник Паскаля.

          1        1     1     1     2     1   1    3     3     1 1   4     6     4     1 

или он же, но немного в другом виде. В левой колонке строки значение n, дальше в строке значения 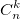для k=0..n

 n          биномиальные коэффициенты  0      1  1      1      1  2      1      2      1  3      1      3      3      1  4      1      4      6      4      1  5      1      5     10     10      5      1  6      1      6     15     20     15      6      1  7      1      7     21     35     35     21      7      1  8      1      8     28     56     70     56     28      8      1  9      1      9     36     84    126    126     84     36      9      1 10      1     10     45    120    210    252    210    120     45     10      1 11      1     11     55    165    330    462    462    330    165     55     11      1 12      1     12     66    220    495    792    924    792    495    220     66     12      1 13      1     13     78    286    715   1287   1716   1716   1287    715    286     78     13      1 14      1     14     91    364   1001   2002   3003   3432   3003   2002   1001    364     91     14      1 15      1     15    105    455   1365   3003   5005   6435   6435   5005   3003   1365    455    105     15      1 16      1     16    120    560   1820   4368   8008  11440  12870  11440   8008   4368   1820    560    120     16      1 

В полном соответствии с рекуррентной формулой значения 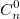равны 1 и любое число равно сумме числа, стоящего над ним и числа «над ним+шаг влево». Например, в 7й строке число 21, а в 6й строке числа 15 и 6: 21=15+6. Видно также, что значения в строке симметричны относительно середины строки, т.е. . Это свойство симметричности бинома Ньютона относительно a и b и оно видно в факториальной формуле.
Ниже для биномиальных коэффициентов 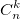я буду также использовать представление C(n,k) (его проще набирать, да и формулу-картинку не везде можно вставить.

Расчет биномиальных коэффициентов через факториальную формулу

поскольку биномиальные коэффициенты неотрицательные, будем использовать в расчетах беззнаковый тип.

// расчет факториала n unsigned fakt(int n) {    for (unsigned r=1;n>0;--n)            r*=n;    return r; } // расчет C(n,k) unsinged bci(int n,int k) {    return fakt(n)/(fakt(k)*fakt(n-k)); } 

Вызовем функцию bci(10,4) — она вернет 210 и это правильное значение коэффициента C(10,4). Значит, задача расчета решена? Да, решена. Но не совсем. Мы не ответили на вопрос: при каких максимальных значениях n,k функция bci будет работать правильно? Прежде чем начать искать ответ, условимся, что используемый нами тип unsigned int 4-х байтный и максимальное значение равно 2³²-1=4’294’967’295. При каких n,k C(n,k) превысит его? Обратимся к треугольнику Паскаля. Видно, что максимальные значения достигаются в середине строки, т.е. при k=n/2. Если n четно, то имеется одно максимальное значение, а если n нечетно, то их два. Точное значение C(34,17) равно 2333606220, а точное значение C(35,17) равно 4537567650, т.е. уже больше максимального unsigned int.
Напишем тестовую процедуру

void test() {     for (n=10;n<=36;++n)      printf("%u %u",n,bci(n,n/2);  // для C++ можно использовать cout<<n<<" "<<bci(n,n/2)<<endl; } 

10 252 11 462 12 924 13 532 14 50 15 9 16 1 17 2 18 1 19 0 20 0 21 1 22 0 23 4 24 1 25 0 26 1 27 0 28 1 29 0 30 0 31 0 32 2 33 2 34 0 35 0 

Значение в очередной строке должно быть примерно в 2 база больше, чем в предыдущей. Поэтому последний правильно вычисленный коэффициент (см треугольник выше) — это C(12,6) Хотя unsigned int вмещает 4млрд, правильно вычисляются значения меньше 1000. Вот те раз, почему так? Все дело в нашей процедуре bci, точнее в строке, которая сначала вычисляет большое число в числителе, а потом делит его на большое число в знаменателе. Для вычисления C(13,6) сначала вычисляется 13!, а это число > 6млрд и оно не влезает в unsigned int.
Как оптимизировать расчет 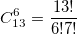? Очень просто: раскроем 13! и сократим числитель и знаменатель на 7!.. В результате получится 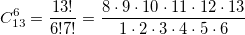. Запрограммируем расчет по этой формуле

unsigned bci(int n,int k)  { 	if (k>n/2) k=n-k; // возьмем минимальное из k, n-k.. В силу симметричность C(n,k)=C(n,n-k) 	if (k==1)  return n; 	if (k==0)  return 1; 	unsigned r=1; 	for (int i=1; i<=k;++i) { 		r*=n-k+i; 		r/=i; 	} 	return r; } 

:

10 252 11 462 12 924 13 1716 14 3432 15 6435 16 12870 17 24310 18 48620 19 92378 20 184756 21 352716 22 705432 23 1352078 24 2704156 25 5200300 26 10400600 27 20058300 28 40116600 29 77558760 30 155117520 31 14209041 32 28418082 33 39374192 34 78748384 35 79433695 

Явно лучше, ошибка возникла при расчете C(31,15). Причина понятна — все то же переполнение. Сначала умножаем на 31 (оп-па — переполнение, потом делим на 15). А что, если использовать рекурсивную формулу? Там только сложение, переполнения быть не должно.
Что ж, пробуем:

unsigned bcr(int n,int k)  { 	if (k>n/2) k=n-k; 	if (k==1)  return n; 	if (k==0)  return 1; 	return bcr(n-1,k)+bcr(n-1,k-1); } void test() {     for (n=10;n<=36;++n)      printf("%u %u",n,bcr(n,n/2);  // для C++ можно использовать cout<<n<<" "<<bcr(n,n/2)<<endl; } 

10 252 11 462 12 924 13 1716 14 3432 15 6435 16 12870 17 24310 18 48620 19 92378 20 184756 21 352716 22 705432 23 1352078 24 2704156 25 5200300 26 10400600 27 20058300 28 40116600 29 77558760 30 155117520 31 300540195 32 601080390 33 1166803110 34 2333606220 35 242600354 

Все, что влезло в unsigned int, посчиталось правильно. Вот только строчка с n=34 считалась около минуты. При расчете C(n,n/2) делается два рекурсивных вызова, поэтому время расчета экспоненциально зависит от n. Что же делать — получается либо неточно, либо медленно. Выход — в использовании 64 битных переменных.

Использование 64 битных типов для расчета C(n,k)

Заменим в функции bci unsigned int на unsigned long long и протестируем в диапазоне n=34..68. n=34 — это максимальное значение, которое правильно считается bci, а C(68,34) ~2.8*10¹⁹ уже не влезает в unsigned long long ~1.84*10¹⁹

unsigned long long bcl(int n,int k)  { 	if (k>n/2) k=n-k; 	if (k==1)  return n; 	if (k==0)  return 1; 	unsigned long long r=1; 	for (int i=1; i<=k;++i) { 		r*=n-k+i; 		r/=i; 	} 	return r; }  void test() {     for (n=34;n<=36;++n)      printf("%llu %llu",n,bcl(n,n/2));  // для C++ можно использовать cout<<n<<" "<<bcl(n,n/2)<<endl; }  

34 2333606220 35 4537567650 36 9075135300 37 17672631900 38 35345263800 39 68923264410 40 137846528820 41 269128937220 42 538257874440 43 1052049481860 44 2104098963720 45 4116715363800 46 8233430727600 47 16123801841550 48 32247603683100 49 63205303218876 50 126410606437752 51 247959266474052 52 495918532948104 53 973469712824056 54 1946939425648112 55 3824345300380220 56 7648690600760440 57 15033633249770520 58 30067266499541040 59 59132290782430712 60 118264581564861424 61 232714176627630544 62 465428353255261088 63 321255810029051666 64 66050867754679844 65 454676336121653775 66 350360427585442349 67 23341572944240599 68 46683145888481198 

Видим, что ошибка возникает при n=63 по той же причине, что и в bci. Сначала умножение на 63 (и переполнение), затем деление на 31.

Дальнейшее повышение точности и расчет при n>67

Ошибка возникла при n=63, а при n=68 уже не влезает в unsigned64. Поэтому можно сказать «до n<=62 функция bcl считает правильно, дальнейшее увеличение точности требует либо inе128 либо длинной арифметики». А если очень высокая точность не нужна, но хочется считать биномиальные коэффициенты при n=100…1000? Снова берем процедуру bci и меняем в ней типы unsigned int на double:

double bcd(int n,int k)  { 	if (k>n/2) k=n-k; // возьмем минимальное из k, n-k.. В силу симметричности C(n,k)=C(n,n-k) 	if (k==1)  return n; 	if (k==0)  return 1; 	double r=1; 	for (int i=1; i<=k;++i) { 		r*=n-k+i; 		r/=i; 	} 	return ceil(r-0.2); // округлим до ближайшего целого, отбросив дробную часть } void testd() {     for (n=50;n<=1000;n+=50)      printf("%llf %llf",n,bcd(n,n/2));  // для C++ можно использовать cout<<n<<" "<<bcd(n,n/2)<<endl; } 

Даже для n=1000 удалось посчитать! Переполнение double произойдет при n=1030.
Расхождение расчета bcd с точным значением начинается с n=57. Он небольшое — всего 8. При n=67 отклонение 896.

Для экстремалов и «олимпийцев»

В принципе, для практических задач точности функции bcd достаточно, но в олимпиадных задачах часто даются тесты «на грани». Т.е. теоретически может встретится задача, где C(n,k) влезает в unsignerd long long еле-еле. Как избежать переполнения для таких крайних случаев? Можно использовать рекурсивный алгоритм. Но если он для n=35 считал минуту, то для n=67 будет считать лет 100. Однако можно использовать рекурсию не для всех n и k, а только для «достаточно больших». Вот процедура расчета, которая считает правильно для n<=67. Иногда и для n>67 при малых k (к примеру, считает C(82,21)=1.83*10¹⁹).

unsigned long long bcl(int n,int k)  { 	if (k>n/2) k=n-k; 	if (k==1)  return n; 	if (k==0)  return 1; 	unsigned long long r; 	if (n+k>=90) { 		// разрядности может не хватить, используем рекурсию 		r=bcl(n-1,k); 		r+=+bcl(n-1,k-1); 	} 	else { 		r=1; 		for (int i=1; i<=k;++i) { 			r*=n-k+i; 			r/=i; 		} 	} 	return r; } 

В какой-то из олимпиадных задач мне потребовалось вычислять много C(n,k) для n >70, т.е. они заведомо не влезали в unsigned long long. Естественно, пришлось использовать «длинную арифметику» (свою). Для этой задачи я написал «рекурсию с памятью»: вычисленные коэффициенты запоминались в массиве и экспоненциального роста времени расчета не было.

ссылка на оригинал статьи http://habrahabr.ru/post/274689/