В статье описывается реализация известного метода конечных объемов для численного решения уравнений в частных производных.Используется разбиение области на любые стандартные элементы(конечные объемы) — треугольники, четырехугольники и т.д.Метод визуализации результатов расчетов также самописный.
Метод Finite Volume (FVM)
В основе метода лежит разбиение области на непересекающиеся контрольные объемы(элементы), узловые точки, в которых ищется решение.Узловые точки находятся в центрах контрольных объемов.Также, как и для метода конечных разностей, для каждого элемента составляется уравнение, получается система линейных уравнений.Решая ее — находим значения
искомых переменных в узловых точках.Для отдельного элемента уравнение получается путем интегрирования исходного дифф уравнения по элементу и аппроксимации интегралов.
Термин конечный объем в статье будет часто заменятся на Элемент, будем для удобства считать их эквивалентами (элемент в данной статье не имеет ничего общего с методом конечных элементов).
Есть 2 различных способа решения задачи по FVM:
1) грани контрольного объема совпадают с гранями элемента
2) грани контрольного объема проходят через центры граней элементов(на которые разбита область).Искомые переменные хранятся в вершинах этих элементов.Вокруг каждой вершины строится контрольный объем. Для непрямоугольной сетки этот способ имеет еще 2 подвида.

Мы будем использовать способ 1) с контрольными объемами совпадающими с элементами на которые разбита область.
Некоторые плюсы FVM:
- сохранение основных величин по всей области, таких как энергия системы, масса, тепловые потоки и тд.Причом это условие выполняется даже для грубой расчетной сетки
- высокая скорость расчета.Многие расчетные величины можно вычислить при разбиении области на элементы, и вычислять их на каждом шаге по времени нет необходимости.
- легкость использования для задач со сложной геометрией и криволинейными границами.Легкость использования разных геометрических типов элементов — треугольники, полигоны.
Метод FVM реализуем на примере уравнения теплопроводности:
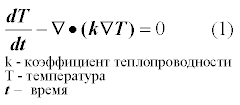
Итак основные шаги при реализации FVM:
- Перевод дифф уравнения в форму пригодную для FVM — интегрирование по контрольному объему
- Составление дискретного аналога, выбор способа перевода производных и других подынтегральных выражений в дискретную форму
- Получение уравнения для каждого из контрольных объемов, на которые разбита область.Составление системы линейных уравнений и ее решение.
Дискретизация по времени.
Для производной по времени используем стандартный простейший метод Эйлера.Это будет явная схема по времени, где берутся искомые с предыдущего шага.А на первом шаге задаются как начальные условия.

Немного теории или первый шаг в реализации FVM
Используя теорему о дивергенции интеграл по объему преобразуется в интеграл по площади.Смысл в том что интегрирование по всему внутреннему объему нашего элемента мы заменяем на интегрирование только по поверхности этого объема.Эта формулировка больше подходит для 3D случая.Для 2D у нас будет вместо объема V — площадь элемента, а вместо S — периметр элемента.Тоесть получается что интеграл по площади заменяется интегралом по периметру.Фактически у нас понижается степень производной.Если например была вторая производная то остается только первая, если была первая — то вместо производной будет искомая переменная.Надо только не забывать что имеем дело не с обычной производной а с дивергенцией.
Итак второй терм в нашем уравнении после интегрирования преобразуется так:
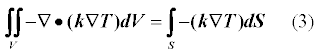
FVM на стандартной прямоугольной сетке

На рисунке изображен Элемент С и его соседние элементы справа(E), слева(W), сверху(N) и снизу(S).У элемента С есть 4 грани обозначенные буквами e w n s.Именно эти 4 грани и составляют периметр элемента и по ним производится интегрирование.Для каждого элемента в результате получаем дискретный аналог исходного дифф уравнения.
Составим дискретный аналог для элемента С.Для начала нужно разобраться с интегралом (3).Интеграл это ведь по факту сумма.Поэтому мы и заменяем интеграл по всей поверхности элемента, на сумму по 4-м составляющим этой поверхности, тоесть 4 граням элемента.
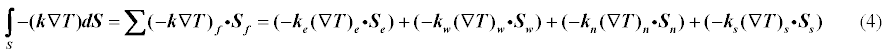
Индексы e w n s здесь обозначают что выражение или переменная вычисляется в центре соответствующей грани.
Теперь соберем вместе полученные упрощения частей исходного дифф уравнения — термы (2) и (4).Получим первую ступень аппроксимации:

Теперь нам осталось только до конца аппроксимировать (4), поскольку туда входит градиент, его то нам и надо перевести в численную форму.Фактически эта сумма представляет сумму потоков тепла через грани.Наш случай упрощается для прямоугольной сетки, т.к у нормали к грани остается только 1 компонент — либо вдоль оси х либо вдоль y.
Разберем подробно этот процесс на примере грани e.

Теперь подставим вместо суммы в уравнении (5) полученные дискретные аналоги для 4-х граней:
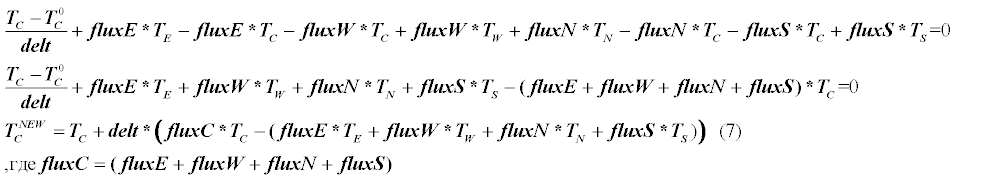
Уравнение (7) и есть конечное уравнение для элемента С, из него мы на каждом шаге по времени получаем новое значение температуры (Tnew) в элементе С.
Граничные условия на прямоугольной сетке
На рисунке показан элемент С у которого грань e находится на границе и значения температуры на этой грани известны — либо как заданная температура либо как заданный поток тепла через грань.

Мы рассмотрим только 2 вида граничных условий.
- Задана температура Tb на границе
- Задан поток FluxB на границе, рассмотрим только случай когда FluxB=0, т.е. грань e будет теплоизолирована(Insulated)
Случай 2) самый простой, поскольку получается что грань e не потребуется при дискретизации(т.к. все коэффициенты Flux=0) и можно ее просто пропустить.
Теперь рассмотрим случай 1).Дискретизация грани e будет в целом похожа на ту что уже была описана.Будут только 2 изменения — вместо Te будет известное граничное значение Tb и вместо расстояния DXe будет DXe/2.В остальном можно рассматривать значение Te так, как будто это был бы обычный соседний узел E.Теперь подробнее распишем терм для граничного элемента С.
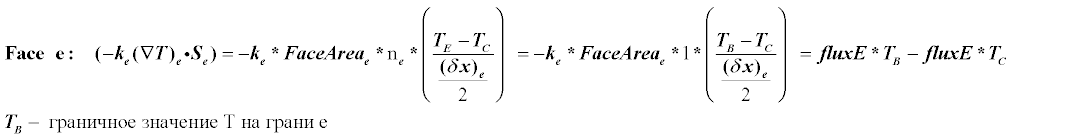
Пример численных расчетов на прямоугольной сетке
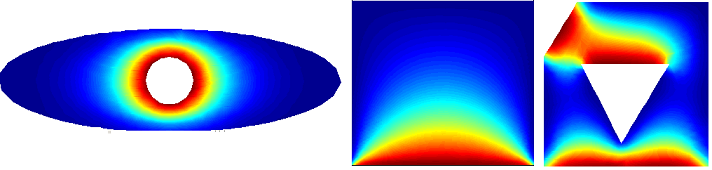
В качестве примера рассмотрим область разбитую на 9 элементов, сетка 3*3.На первых слайдах применены следующие граничные условия: по 3 сторонам температура T=0, снизу задана температура T=240.На второй строке слайдов по бокам заданы граничные условия с потоком Flux=0, сверху T=0, снизу T=240.По каждому случаю 2 картинки, одна с разбивкой области 3*3 элемента, вторая 40*40.
public void RunPhysic() { double Tc, Te, Tw, Tn, Ts; double FluxC, FluxE, FluxW, FluxN, FluxS; double dx = 0; double Tb = 240; double Tb0 = 0; int i, j; for (i = 0; i < imax; i++) for (j = 0; j < jmax; j++) { Tc = T[i, j]; dx = dh; if (i == imax - 1) { Te = Tb0; dx = dx / 2; } else Te = T[i + 1, j]; FluxE = (-k * FaceArea) / dx; if (i == 0) { Tw = Tb0; dx = dx / 2; } else Tw = T[i - 1, j]; FluxW = (-k * FaceArea) / dx; if (j == jmax - 1) { Tn = Tb0; dx = dx / 2; } else Tn = T[i, j + 1]; FluxN = (-k * FaceArea) / dx; if (j == 0) { Ts = Tb; dx = dx / 2; } else Ts = T[i, j - 1]; FluxS = (-k * FaceArea) / dx; FluxC = FluxE + FluxW + FluxN + FluxS; T[i, j] = Tc + delt * (FluxC * Tc - (FluxE * Te + FluxW * Tw + FluxN * Tn + FluxS * Ts)); } } //Insulated public void RunPhysic2() { double Tc, Te, Tw, Tn, Ts; double FluxC, FluxE, FluxW, FluxN, FluxS; double dx = 0; double Tb = 240; double Tb0 = 0; int i, j; for (i = 0; i < imax; i++) for (j = 0; j < jmax; j++) { Tc = T[i, j]; dx = dh; Te = 0; Tw = 0; if (i == imax - 1) FluxE = 0; else { Te = T[i + 1, j]; FluxE = (-k * FaceArea) / dx; } if (i == 0) FluxW = 0; else { Tw = T[i - 1, j]; FluxW = (-k * FaceArea) / dx; } if (j == jmax - 1) { Tn = Tb0; dx = dx / 2; } else Tn = T[i, j + 1]; FluxN = (-k * FaceArea) / dx; if (j == 0) { Ts = Tb; dx = dx / 2; } else Ts = T[i, j - 1]; FluxS = (-k * FaceArea) / dx; FluxC = FluxE + FluxW + FluxN + FluxS; T[i, j] = Tc + delt * (FluxC * Tc - (FluxE * Te + FluxW * Tw + FluxN * Tn + FluxS * Ts)); } }

FVM в задачах со сложной геометрией
Здесь как раз проявляется преимущество FVM, где также, как и в методе конечных элементов, можно представлять область с круглыми границами через разбиение на треугольники или любые другие полигоны.Но FVM имеет еще 1 плюс — при переходе от треугольников к полигонам с большим числом сторон не требуется абсолютно ничего менять, конечно если код был написан для произвольного треугольника а не равностороннего.Более того, можно без изменения кода использовать смесь разных элементов — треугольники, полигоны, квадраты и тд.
Рассмотрим общий случай, когда вектор соединяющий центры 2-х элементов не совпадает с вектором нормали к общей грани этих элементов.Вычисление потока flux через грань теперь будет состоять из 2-х частей.В первой будет расcчитываться ортогональная составляющая а во второй так называемая «кросс-диффузия».
На картинке изображены 2 элемента, С — текущий рассматриваемый элемент и F — соседний элемент.Опишем дискретизацию для грани, разделяющей эти 2 элемента.Вектор соединяющий центры элементов — DCF.Вектор e — это единичный вектор по направлению DCF.Вектор Sf — направлен по нормали к грани, его длинна равна длине грани.

Схема расчетов выглядит примерно так.

Второй терм здесь это кросс-диффузия, она будет тем больше, чем больше расхождение между векторами Ef и Sf, если они совпадают, то она равна 0.
Распишем сначала ортогональную часть(способ minimum correction).

В исходниках я не стал реализовывать терм с кроссдиффузией, т.к встал вопрос — как проверить корректность такой реализации.Визуально сравнение результатов Матлаб и моих ничем не отличалось в отсутствии кросс-диффузии.Видимо это связано с тем что Матлаб любит треугольники близкие к равносторонним, что в итоге делает кроссдиффузию=0.Возможно позже еще вернусь к этому вопросу.
Расчет граничных элементов ничем не отличается от расчетов не на границе, вместо центра соседнего элемента берется центр грани, ну и как обычно подставляется температура на границе.
В моей реализации в итоге получается так:
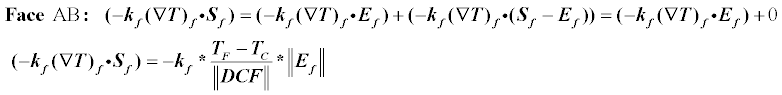
public void Calc() { double bc, ac; double sumflux; double[] aa = new double[6]; double[] bb = new double[6]; int e; for (e = 0; e < elementcount; e++) { Element elem = elements[e]; int nf; bc = 0; ac = 0; sumflux = 0; for (int nn = 0; nn <6; nn++) { aa[nn] = 0; bb[nn] = 0; } for (nf = 0; nf < elem.vertex.Length; nf++) { Face face = elem.faces[nf]; Element nb = elem.nbs[nf]; if (face.isboundary) { if (face.boundaryType == BoundaryType.BND_CONST) { double flux1; double flux; flux1 = elem.k * (face.area / elem.nodedistances[nf]); Vector2 Sf = face.sf.Clone(); Vector2 dCf = elem.cfdistance[nf].Clone(); if (Sf * dCf < 0) Sf = -Sf; //1) minimum correction //Vector2 DCF = elem.cndistance[nf].Clone(); Vector2 e1 = dCf.GetNormalize(); Vector2 EF = (e1 * Sf) * e1; flux = elem.k * (EF.Length() / dCf.Length()); ac += flux; bc += flux * face.bndu; bb[nf] = flux; } else if (face.boundaryType == BoundaryType.BND_INSULATED) { double flux; flux = 0; ac += flux; bc += flux * face.bndu; bb[nf] = flux; } } else { double flux1; double flux; flux1 = -elem.k * (face.area / elem.nodedistances[nf]); Vector2 Sf = face.sf.Clone(); Vector2 dCf = elem.cfdistance[nf].Clone(); if (Sf * dCf < 0) Sf = -Sf; Vector2 DCF = elem.cndistance[nf].Clone(); Vector2 e1 = DCF.GetNormalize(); //corrected flux //1) minimum correction Vector2 EF = (e1 * Sf) * e1; flux = -elem.k * (EF.Length() / DCF.Length()); sumflux += flux * nb.u; ac += -flux; aa[nf] = -flux; } } elem.u = elem.u + delt * (bc - sumflux - ac * elem.u); } }
Примеры и проверка результатов
Проверка проводилась сравнением результатов в Матлаб и моей реализации. Mesh использовалась одинаковая, выгружалась из Матлаб и загружалась в прогу.На некоторые артефакты-треугольники не обращайте внимания, это просто непонятный глюк отрисовки.

Описание структуры исходников
Гитхаб с исходниками лежит тут
Основная версия в папке heat2PolyV2.То что относится к вычислительной части лежит в heat2PolyV2\Src\FiniteVolume\.
Вначале файла Scene2.cs — параметры которые можно менять для отображения в разных цветовых схемах, масштаб, отображение mesh и т.д.Сами примеры хранятся в heat2PolyV2\bin\Debug\Demos\
Выгрузку из Матлаба сделать просто — нужно открыть pde toolbox, открыть m файл (либо создать самому с нуля), зайти в меню Mesh-Экспорт mesh, нажать ОК; перейти в основной Матлаб, в панельке появятся переменные — матрицы p e t, открыть файл savemymesh.m, выполнить его, появится файл p.out, перенести его в папку Demos.
В исходниках для выбора примера необходимо задать имя файла в строке param.file = «p»;(FormParam.cs).Далее необходимо применить граничные условия — для готовых примеров можно просто раскомментировать соответствующие блоки в MainSolver.cs:
//p.out public void SetPeriodicBoundary() Смысл тут простой — Матлаб разделяет границы по доменам, например внешние и внутренние.Также для каждого домена границы разбиты на части (группы), чтобы можно было задавать условия на участках границы по отдельности — например справа или снизу.
Возможно и вовсе не использовать Матлаб, а вручную прописать все элементы(треугольники) и их вершины + грани(только для граничных элементов)
##Points — координаты точек, первая строка — х, вторая -y.
##Triangle — треугольники, первая строка — индекс 1-ой вершины в массиве ##Points,2 и 3 строки — индексы 2 и 3 вершины треуольника.
##Boundary — грани, первая строка — индекс 1-ой вершины грани ,2-я — индекс второй вершины, пятая строка — группа, шестая — домен
Гитхаб с исходниками
- heat2PolyV2 — финальная версия
- other\heat2Utrianglestatic — реализован пример из книги p346 versteeg_h malalasekra_w_ An_introduction_to_computational_fluid…
- other\water2dV2 — попытка решения уравнений Навье-Стокса частично используя FiniteVolume
- matlab — m файлы примеров pde toolbox + savemymesh.m который выгружает готовый .out файл для heat2PolyV2
- Versteeg HK Malalasek Introduction to computational fluid dynamics The finite volume method — уже есть второе издание
- F.Moukalled L.Mangani M.Darwish The finite volume method in computational fluid dynamics 2016г — вышла недавно (чуть ли не вчера:)
- Патанкар С.-Численные методы решения задач теплообмена и динамики жидкости-Энергоатомиздат (1984)
- Патанкар С.В.-Численное решение задач теплопроводности и конвективного теплообмена при течении в каналах-МЭИ (2003)
- Computational methods for fluid dynamics Ferziger JH Peric 2001 — хоть напрямую и не относится к FVM, но оч много полезного
ссылка на оригинал статьи https://habrahabr.ru/post/276193/
Добавить комментарий